杭州学军中学信友队趣味网络邀请赛 总结
这次比赛我只考了148148148分,虽然题目很难,但是还是考得不错,可以算是中山市小学生前555名吧。这一次我就只做了前两题,后面的我就不讲了。
第一题 题目:
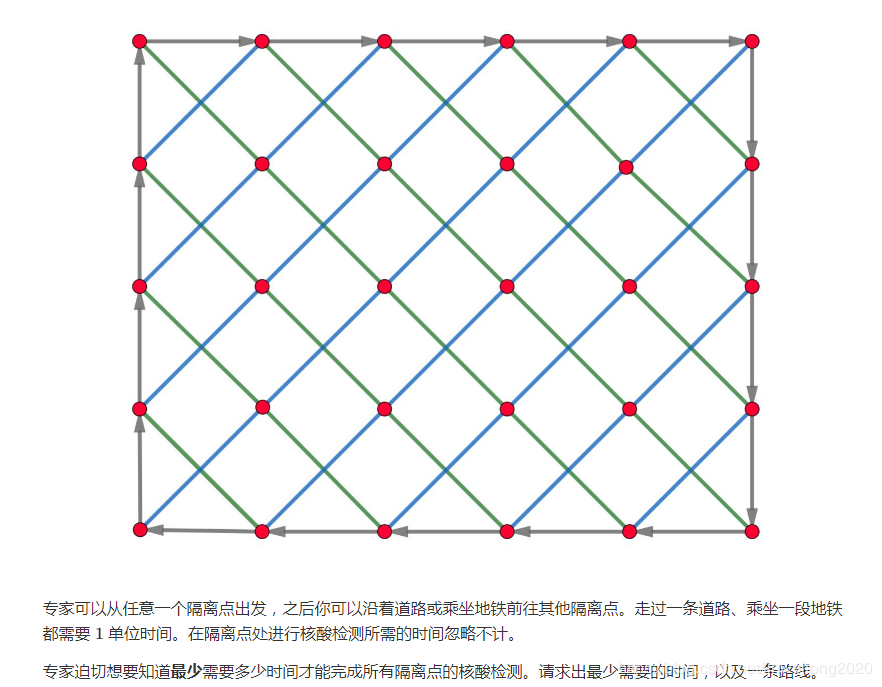

这道题其实很简单,主要的方法就是找规律,我也是在444点半才找到规律的。我们多试几个例子,就可以找出。
对于子任务111我们可以直接用上面的样例来做,直接打表 。
可以在草稿纸上画一下,就可以得出了。
对于子任务333~555 第一种方法——搜索:可以用搜索来模拟这个图,应该只能拿到505050分左右。
第二种方法——数学(正解):我们可以发现,当nnn是偶数时:

当nnn是奇数时:

其实他们都是按照这种方式的——就是缠绕法:

发现规律之后,我们直接模拟就可以了。
比赛时100100100分。
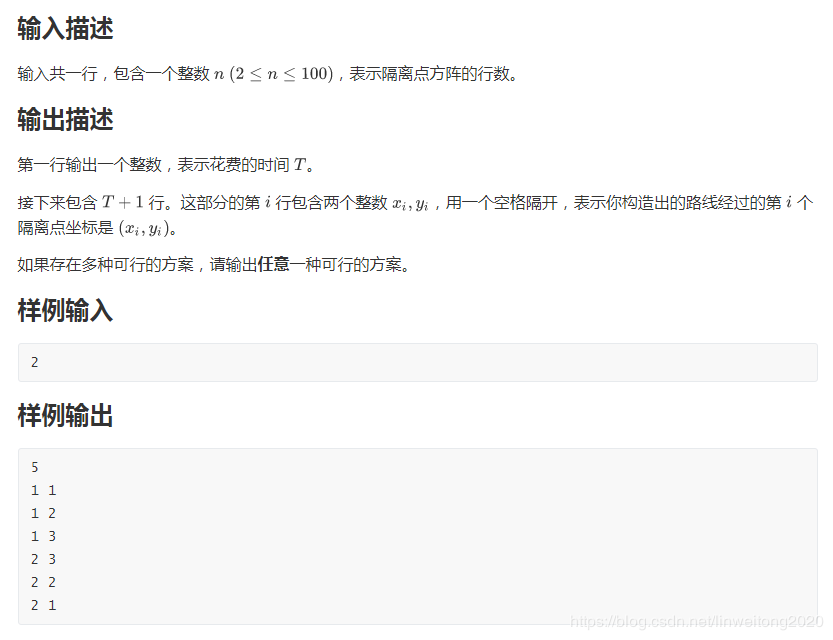
第二题 题目:
这道题目比较简单理解,但是想拿满分不容易。
对于子任务111对于子任务111,因为n=2n=2n=2,所以我们直接比较答案就行了。
对于子任务222对于子任务222,我们可以打一个三重循环来过这道题,时间复杂度为O(n3)O(n^3)O(n3)。
当然我也得了这么多分,但是我用的是spfaspfaspfa,时间复杂度是O(n2)O(n^2)O(n2),可能是因为spfaspfaspfa的常数太大了,所以没有过子任务333。
怎么求两个点的距离呢?
首先我们引入一个概念,LCALCALCA,意思是最近公共祖先。
我们如何求两个点的LCALCALCA呢?
直接让两个点分别往上跳就行了。
倍增求LCALCALCA我们设fi,jf_{i,j}fi,j表示结点iii的2j2^j2j辈祖宗。
那么
fi,0=faf_{i,0}=fafi,0=fa
fi,j=ffi,j−1,j−1(j>0)f_{i,j}=f_{f_{i,j-1},j-1}(j>0)fi,j=ffi,j−1,j−1(j>0)
注:fafafa表示结点iii的父亲。
那么我们只用进行二进制拆分就可以算出LCALCALCA了。
我们求完LCALCALCA之后,就要求深度(后面有用)。
我们设depxdep_xdepx表示结点xxx的深度。
则
depx=depfa+1dep_x=dep_{fa}+1depx=depfa+1
我们求出了LCALCALCA,就可以算出距离。
现在我们要求xxx和yyy的最短路径,那么
dis(x,y)=depx+depy−2depLCA(x,y)dis(x,y)=dep_x+dep_y-2dep_{LCA(x,y)}dis(x,y)=depx+depy−2depLCA(x,y)
注:dis(x,y)dis(x,y)dis(x,y)表示xxx到yyy的最短距离。
那么现在我们就可以用O(n2logn2)O(n^2\log^2_n)O(n2logn2)的时间算出答案。
对于子任务444(满分)怎么才能的满分呢?
其实很简单。
我们重新看一下题目,题目可以变为:使max(x,y)×dis(x,y)max(x,y)\times dis(x,y)max(x,y)×dis(x,y)最大。
那么我们其实把max(x,y)×dis(x,y)max(x,y)\times dis(x,y)max(x,y)×dis(x,y)拆成
max(x×dis(x,y),y×dis(x,y))max(x\times dis(x,y),y\times dis(x,y))max(x×dis(x,y),y×dis(x,y))。
怎么才能使dis(x,y)dis(x,y)dis(x,y)最大呢?
我们引入“树的直径”。
树上最长的一条路。
树的直径的性质 这条路的两个端点一定是叶结点 这条路一定经过根节点 证明:现在我们要证明任意一个点到树的直径的两个端点(其中一个)的距离最远。
我们假设uuu和vvv是树的直径上的两个端点,xxx为任意一个结点。
如下:
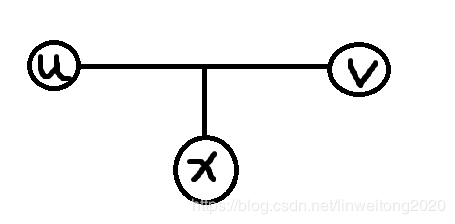
我们用反证法。
假设有一个结点yyy,并且满足xxx与结点yyy的距离还要比xxx与vvv的距离远。
如下:
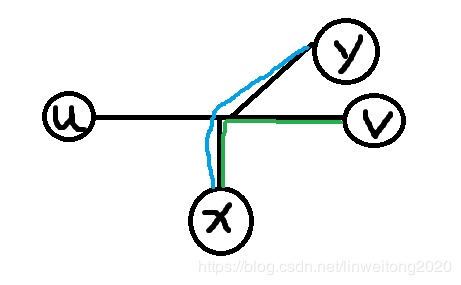
也就是蓝色线比绿色线要长。
那么我们把公共部分删掉。得:

这时候在把线延长至uuu点。得:

上面这张图显示:dis(u,y)>dis(u,v)dis(u,y)>dis(u,v)dis(u,y)>dis(u,v)。
但是我们知道dis(u,v)dis(u,v)dis(u,v)是最长路径,怎么可能还比它大呢?
所以,有矛盾。
因此得出,任意一个点到树的直径的两个端点(其中一个)的距离最远。
那么我们直接求出直径端点到每个点的距离,再比较就行了。
得分情况:得了484848分,对了前222个点。
改题后100100100分。


我们可以直接用状压dpdpdp来做,时间复杂度为O(2n×poly(n))O(2^n\times poly(n))O(2n×poly(n))。
对于子任务222可以优化,时间复杂度为O(n4)O(n^4)O(n4),可以过。
对于子任务333对上面的方法进行前缀和优化,时间复杂度为O(n3)O(n^3)O(n3)。
对于子任务444可以先用完全背包预处理,时间复杂度为O(n2)O(n^2)O(n2)。
得分情况:考试时没有做。
改题之后答案错误,还是000分。

首先有一个暴力算法。记A(i,j)A(i,j)A(i,j)为当前还有iii点行动值,上轮的行动值为 jjj时的胜败情况,可以使用动态规划O(n2)O(n^2)O(n2)计算出所有的 hmh_mhm。
A(i−k,k)→A(i,j)A(i-k,k)\rightarrow A(i,j)A(i−k,k)→A(i,j)
首先,如果mmm为奇数,那么人类方只要在第一轮中只付出一点行动值就能获胜,因为接下来双方都只能每轮付出一点行动值。
而如果mmm为偶数,那么人类方第一轮的行动值必须为偶数,否则轮到病毒方时剩余行动值就会变成奇数。由此我们得出,如果mmm为偶数,双方每次的行动值都一定为偶数。那么只要把每两点行动值合并,我们就能得到h2m=2hmh_{2m}=2h_mh2m=2hm。
我们可以得到
hm={1,m=2n+12hn,m=2nh_m=\begin{cases}
1,{m=2n+1} \\
{2h_n},{m=2n}
\end{cases}hm={1,m=2n+12hn,m=2n
不难得出hm=max2k∣m2kh_m=\max_{2^k|m}{2^k}hm=max2k∣m2k,即hm=lowbit(m)h_m=lowbit(m)hm=lowbit(m)。
注:lowbit(x)lowbit(x)lowbit(x)是xxx的二进制表达式中最低位的111所对应的值。
直接用O(n)O(n)O(n)计算出所有hmh_mhm。
对于子任务444或555没有看懂 ,大佬请谅解。


比赛时没做。
改题之后101010分。


国家队层次的题目,没有读懂。
正解:线段树+凸包。
题解图片:

作者:linweitong2020