我所理解的协方差以及协方差矩阵
定义:假如有N个样本的集合{X1,X2,...XNX_1,X_2,...X_NX1,X2,...XN},我们可以定义出以下定义。
 1.均值">
1.均值">
标准差是用来描述离散程度,。之所以除以n-1而不是除以n,是因为这样能使我们以较小的样本集更好的逼近总体的标准差,即统计上所谓的“无偏估计”。而方差则仅仅是标准差的平方。
标准差和方差一般是用来描述一维数据的,协方差就是这样一种用来度量两个随机变量关系的统计量
仿照方差的定义
可以这样定义协方差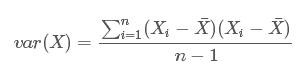
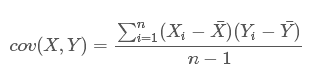
来度量各个维度偏离其均值的程度。
两个或者两个以上的随机变量函数的情况
设ZZZ是随机变量X,YX,YX,Y的函数Z=g(X,Y),Z=g(X,Y),Z=g(X,Y),(ggg是连续函数),那么ZZZ是一个一维随机变量,若二维随机变量(X,Y)(X,Y)(X,Y)的概率密度为f(x,y)f(x,y)f(x,y),则有,E(Z)=E[g(X,Y)]=∫−∞+∞∫−∞+∞g(x,y)f(x,y)dxdyE(Z)=E[g(X,Y)]=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}g(x,y)f(x,y) dxdyE(Z)=E[g(X,Y)]=∫−∞+∞∫−∞+∞g(x,y)f(x,y)dxdy
若(X,Y)(X,Y)(X,Y)为离散型随机变量,其分布律为P{X=xi,Y=yj}=pij,i,j=1,2,⋯ ,P\{X=x_i,Y=y_j\}=p_{ij},i,j=1,2,\cdots,P{X=xi,Y=yj}=pij,i,j=1,2,⋯,则有E(Z)=E[g(X,Y)]=∑j=1∞∑i=1∞g(xi,yj)pijE(Z)=E[g(X,Y)]=\sum_{j=1}^\infty\sum_{i=1}^\infty g(x_i,y_j)p_{ij}E(Z)=E[g(X,Y)]=j=1∑∞i=1∑∞g(xi,yj)pij
故有:cov(X,Y)=∑i=1n(Xi−X‾)(Yi−Y‾)n=E[(X−E(X))(Y−E(Y))]cov(X,Y)={\frac{\sum_{i=1}^n(X_i-\overline X)(Y_i-\overline Y)}{n}}=E[(X-E(X))(Y-E(Y))]cov(X,Y)=n∑i=1n(Xi−X)(Yi−Y)=E[(X−E(X))(Y−E(Y))]
注意这里字母写成n是为了推出期望表达式。
矩阵中的数据按行排列与按列排列求出的协方差矩阵是不同的,这里默认数据是按行排列。即每一行是一个observation(or sample),那么每一列就是一个随机变量。
Xm×n=[a11a12⋯a1na21a22⋯a2n⋮⋮⋱⋮am1am2⋯amn]=[c1,c2,⋯ ,cn]X_{m\times n}=
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2}& \cdots & a_{mn} \\
\end{bmatrix}=[c_1,c_2,\cdots,c_n]
Xm×n=⎣⎢⎢⎢⎡a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn⎦⎥⎥⎥⎤=[c1,c2,⋯,cn]
则协方差矩阵为
[cov(c1,c1)cov(c1,c2)⋯cov(c1,cn)cov(c2,c1)cov(c2,c2)⋯cov(c2,cn)⋮⋮⋱⋮cov(cn,c1)cov(cn,c2)⋯cov(cn,cn)]
\begin{bmatrix}
cov(c_1,c_1)&cov(c_1,c_2)&\cdots&cov(c_1,c_n)\\
cov(c_2,c_1)&cov(c_2,c_2)&\cdots&cov(c_2,c_n)\\
\vdots & \vdots & \ddots & \vdots \\
cov(c_n,c_1)&cov(c_n,c_2)&\cdots&cov(c_n,c_n)\\
\end{bmatrix}
⎣⎢⎢⎢⎡cov(c1,c1)cov(c2,c1)⋮cov(cn,c1)cov(c1,c2)cov(c2,c2)⋮cov(cn,c2)⋯⋯⋱⋯cov(c1,cn)cov(c2,cn)⋮cov(cn,cn)⎦⎥⎥⎥⎤
协方差矩阵的维度等于随机变量的个数,即每一个 observation 的维度。
协方差矩阵公式推导
参考博客我所理解的协方差矩阵
作者:李大九