计算机视觉实验LAB——照相机标定与位姿计算(上)
我们使用了一个名为GenericCamemra的virtual class类型来定义任何一种相机模型。这一点很重要，你可以品尝到编程的灵魂味道就在这里面: )
C++接口描述了类的行为和功能，而不需要完成类的特定实现。
C++接口是使用抽象类来实现的，抽象类与数据抽象互不混淆，数据抽象是一个把实现细节与相关的数据分离开的概念。
设计抽象类（通常称为 ABC）的目的，是为了给其他类提供一个可以继承的适当的基类。抽象类不能被用于实例化对象，它只能作为接口使用。如果试图实例化一个抽象类的对象，会导致编译错误。
因此，如果一个 ABC 的子类需要被实例化，则必须实现每个虚函数，这也意味着 C++ 支持使用 ABC 声明接口。如果没有在派生类中重写纯虚函数，就尝试实例化该类的对象，会导致编译错误。
可用于实例化对象的类被称为具体类。
基类 GenericCamera 提供了很多不同相机模式共同需要的接口（使用virtual void），在派生类 PerspectiveCamera 和 DistortionCamera 中分别用不同的算法来实现相关计算。
class GenericCamera//基类
{
public:
vpColVector xi_;
GenericCamera() {}
// get the number of intrinsic parameters
unsigned int nbParam() {return xi_.getRows();}
virtual void project(const vpPoint &_P, double &_u, double &_v) = 0;
virtual void computeJacobianIntrinsic(const vpPoint &_P, vpMatrix &_J) = 0;
virtual void computeJacobianExtrinsic(const vpPoint &_P, vpMatrix &_L) = 0;
virtual void updateIntrinsic(const vpColVector &_dxi) = 0;
};
我们可以学习这种设计策略（哈哈，认真体会下面这段引用，我觉得说的很好：）
面向对象的系统可能会使用一个抽象基类为所有的外部应用程序提供一个适当的、通用的、标准化的接口。然后，派生类通过继承抽象基类，就把所有类似的操作都继承下来。
外部应用程序提供的功能（即公有函数）在抽象基类中是以纯虚函数的形式存在的。这些纯虚函数在相应的派生类中被实现。 这个架构也使得新的应用程序可以很容易地被添加到系统中，即使是在系统被定义之后依然可以如此。
现在，我们从这段基类的程序片段来学习相机的建模。
就像人类婴儿清澈透明的眼睛一样重要，相机作为我们机器人一组感知世界的起点，TA的重要性是不言而喻的。
你如果还记得中学物理课学过的小孔成像的原理的话，就不难理解我们如何把三维空间的一个物体投射到一个平面上了。（图片来源机器人学，机器视觉与Matlab算法基础）
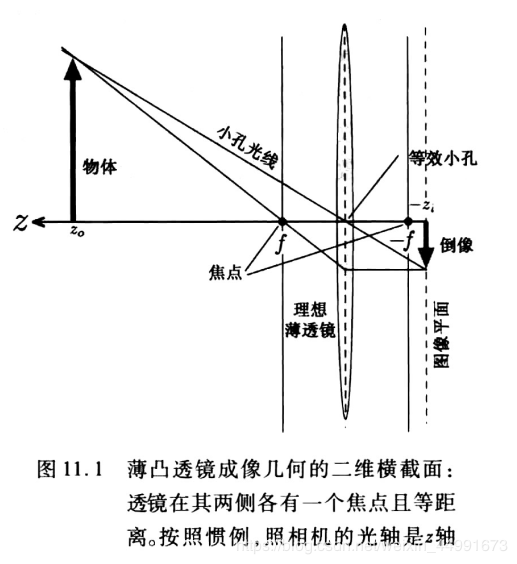
一个小洞察，就像一个小幽默，影响深远。——艾伦.克莱因
下面我们开始分析经典的照相机建模方法如何用照相机实现。
结合中央透视原理和相似三角形数学知识，世界坐标系下某一点P(Xw,Yw,Zw)(X_w,Y_w,Z_w)(Xw,Yw,Zw),齐次表示P~(Xw,Yw,Zw,1)\tilde P(X_w,Y_w,Z_w,1)P~(Xw,Yw,Zw,1)在相机坐标下表示
cP=cTwP^cP = ^cT_wPcP=cTwP
cP=[r11r12r13∣txr21r22r23∣tyr31r32r33∣tz][XwYwZw1]^cP = \begin{bmatrix}
r_11&r_12&r_13&\vert t_x\\
r_21&r_22&r_23&\vert t_y\\
r_31&r_32&r_33&\vert t_z\\
\end{bmatrix}\begin{bmatrix}
X_w\\
Y_w\\
Z_w\\
1
\end{bmatrix}cP=⎣⎡r11r21r31r12r22r32r13r23r33∣tx∣ty∣tz⎦⎤⎣⎢⎢⎡XwYwZw1⎦⎥⎥⎤
然后投射到图像平面xoy上的坐标(x,y)(x,y)(x,y)可求解：
x=fXcZc,y=fYcZcx = f\frac{X_c}{Z_c},y=f\frac{Y_c}{Z_c}x=fZcXc,y=fZcYc
我们把图像平面xoy上的坐标(x,y)(x,y)(x,y)写成齐次形式p~(x′,y′,z′)\tilde p(x',y',z')p~(x′,y′,z′)
x′=fXc,y′=fYc,z′=Zcx'=fX_c,y'=fY_c,z'=Z_cx′=fXc,y′=fYc,z′=Zc
我们写成矩阵的形式如下：
p~=[f000f0001][XcYcZc]
\tilde p =\begin{bmatrix}
f & 0& 0\\
0& f & 0\\
0&0&1
\end{bmatrix}
\begin{bmatrix}
X_c\\
Y_c\\
Z_c
\end{bmatrix}
p~=⎣⎡f000f0001⎦⎤⎣⎡XcYcZc⎦⎤
vpColVector xi_保存的是照相机的内在参数。
parameters: intrinsic parameters (ku,kv,u0,v0,)(k_u,k_v,u_0,v_0,)(ku,kv,u0,v0,), 我们可以从照相机视觉传感器数据手册中获取内在参数，也就是像素尺寸ku,kvk_u,k_vku,kv以及图像平面xoy原点O在像素坐标系下的位置(u0,v0)(u_0,v_0)(u0,v0)（这个参数对于我们从图像平面xoy(x,y)映射到像素空间uov(u,v)(u,v)(u,v)很有帮助）。
u=kufXcZc+u0u = k_uf\frac{X_c}{Z_c}+u_0u=kufZcXc+u0
v=kvYcZc+v0v = k_v\frac{Y_c}{Z_c}+v_0v=kvZcYc+v0
这样，我们就得到了照相机的内在参数矩阵intrinsic matrix (K),
K=[kuf0u00kvv0001]K=\begin{bmatrix}
k_uf&0&u_0\\
0&k_v&v_0\\
0&0&1
\end{bmatrix}K=⎣⎡kuf000kv0u0v01⎦⎤
照相机的外显示参数矩阵就是含有extrinsic parameters (om1,om2,om3,t1,t2,t3)(om_1,om_2,om_3,t_1,t_2,t_3)(om1,om2,om3,t1,t2,t3)的旋转平移矩阵[R∣T][R\vert T][R∣T]，相关空间变换矩阵的性质在计算机视觉入门基础（1）中涵盖。
由此，我们建立起了空间某一点与照相机像素坐标系的关系。
λ[uv1]=K[R∣T][XwYwZw1]\lambda \begin{bmatrix}
u\\
v\\
1
\end{bmatrix}=K[R\vert T]\begin{bmatrix}
X_w\\
Y_w\\
Z_w\\
1
\end{bmatrix}λ⎣⎡uv1⎦⎤=K[R∣T]⎣⎢⎢⎡XwYwZw1⎦⎥⎥⎤
相机标定讲述的是什么故事呢？
相机标定是确定相机在世界坐标系下的外在参数和内在参数的过程。
从相机建模的部分我们已经建立了三维空间一个物体与像素坐标的关系。这便是一个以相机内在参数和外在参数为未知数的非线性方程组求解问题。
λ[uv1]=K[R∣T][XwYwZw1]\lambda \begin{bmatrix}
u\\
v\\
1
\end{bmatrix}=K[R\vert T]\begin{bmatrix}
X_w\\
Y_w\\
Z_w\\
1
\end{bmatrix}λ⎣⎡uv1⎦⎤=K[R∣T]⎣⎢⎢⎡XwYwZw1⎦⎥⎥⎤
求解这一矩阵的数学方法在计算机视觉基础入门（2）中有具体的阐述。
应用VVS(virtual visual serving)相机标定属于非线性过约束的算法，他所求解的方程组个数远大与未知数的个数。拿我们用n张照片的m个点来说，方程组个数为2×m×n2\times m \times n2×m×n,未知数为相机的4个内在参数和6个外在参数。所以，如何进行初始化数据的设置来避免陷入我们最终求解的答案不会是局部最小值很重要。
在我们具体介绍VVS算法之前，我们先来明确:
我们的目标为最小化重投影几何误差(reprojection error),重投影几何误差在计算机视觉领域得到很广泛的应用。TA的含义如下图所示：
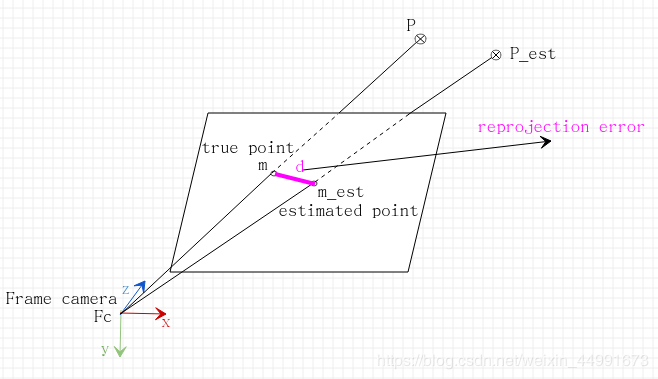我们的重投影误差d是非线性的：
d2=(m−m^)2=(m−PM^)d^2 = (m-\hat m)^2=(m-P\hat M)d2=(m−m^)2=(m−PM^)
我们的目标是如何非线性优化d2d^2d2,典型的方法如下：
Non-linear estimation:gradient descent approach
1.Newton-Raphson
2.Gaussian Newton
3.Levenberg-Marquardt
这些方法的好处在于他们的精确度很好，缺点就是初始点选择不好容易陷入到局部
Minimization is handled using numerical iterative algorithms such as Newton-Raphsonor or Levenberg-Marquartd.The main advantage of these approaches are their accuracy. The maindrawback is that they maybe subject to local minima and worse divergence.Therefore they usually require a good guess of the solution to ensure correct convergence.
非线性优化中，雅可比矩阵的作用不可忽略，TA用来更新参数。
计算相机内在参数和外在参数的雅可比矩阵
作者：肥鼠路易
