兔兔那么好吃！（兔子繁衍+死亡条件）

Cindy ·

更新时间:2024-11-13

· 515 次阅读

最近碰到这么一道题：

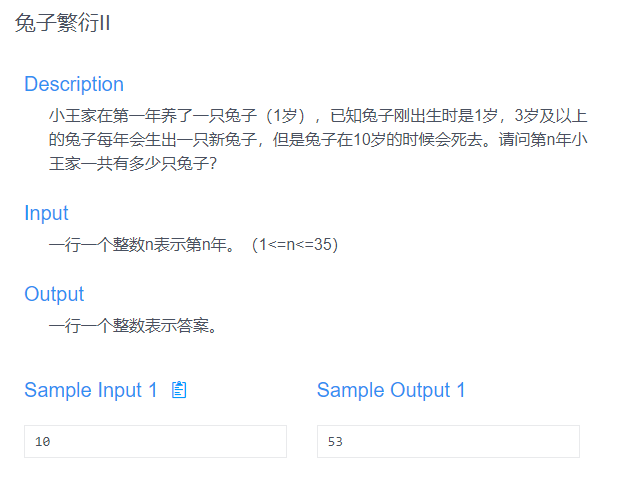
看到题目的第一反应：wtf？？？兔子不用交配就能生小兔子的么？？？

兔子生兔子，初中就学过，斐波那契数列，1123581321：
f(n)=f(n−1)+f(n−2) f(n)=f(n-1)+f(n-2) f(n)=f(n−1)+f(n−2)
这种数学问题在算法题中还算简单，主要靠背（狗头）。

但是这个题加了一个条件，兔子在10岁的时候会死去，这就要考虑到n>10的情况，我尝试在网上搜了一圈，没有搜到靠谱的答案，所以记录下来分享给大家。

Talk cheap, show me code（C语言版）：

int newborn(int n){
    if(n <= 0) return 0;
    if(n == 1) return 1;
    if(n == 2) return 0;
    if(n = 10){
        return newborn(n-2) + newborn(n-1) - newborn(n-9);
    }
}
int f(int n) {
    if(n <= 0) return 0;
    if(n == 1) return 1;
    if(n == 2) return 1;
    if(n = 10){
        return f(n-1) + newborn(n) - newborn(n-9);
    }
}
int main() {
    int n;
    scanf("%d", &n);
    printf("%d", f(n));
    return 0;
}

分析

要解决这个问题，首先要从为什么兔子生兔子是斐波那契数列说起，首先第1年是1只兔子，第1年是0只兔子，第3年是1+1只兔子。。。如下表：

年份	兔子数
1	`1`
2	`1`
3	旧兔子：1，新兔子：1 `1+1=2`
4	旧兔子：2，新兔子：1 `1+2=3`
5	旧兔子：3，新兔子：2 `2+3=5`
6	旧兔子：5，新兔子：3 `3+5=8`
…	…

这个表还是好理解的，看不懂的同学可以给兔子编个号推一遍。由上表可以看出，旧兔子是上一年留下来的，不做什么操作。对兔子数量产生影响的是新出生的兔子，由于规定满三岁才能生小兔子，所以新出生兔子的数量 == 两年前的旧兔子数量。

现在我们形式化定义一下：

设f(n)为第n年的兔子总数量，由上述可得，f(n)=去年旧兔子数量+今年新出生兔子数量，而去年旧兔子数量=f(n-1) and 今年新出生兔子数量=f(n-2)，故
f(n)=f(n−1)+f(n−2) f(n) = f(n-1) + f(n-2) f(n)=f(n−1)+f(n−2)
推到这里相当于复习了一遍初中知识，下面才是重点。

现在引入死亡条件：兔子到10岁就会死，可怜的兔兔，刚出生就1岁了，所以实际上兔兔们只活了9年。那么兔子死了会发生什么呢？死亡会影响两件事：

兔子总数量 -1 死兔子不会生小兔子了，故兔子全家的生育能力 -1，即每年少生一只兔子。

这两件事刚好影响了组成兔子总数量的两个成分，首先，去年旧兔子数量要减去今年死亡兔子数量；其次，今年新出生兔子数量也要减去今年死亡兔子数量，这么说有点拗口，我们形式化定义一下：

设f(n)为今年兔子总数量，newborn(n)为今年新出生兔子数量，death(n)为今年死亡兔子数量。

再想想上面那个条件，兔子只能活9年，故今年死掉的兔子就是9年前新出生的兔子：death(n) = newborn(n-9)，这两式子是等价的。

现在考虑组成兔子总量的两个成分：
去年旧兔子数量=f(n−1)−newborn(n−9) 去年旧兔子数量 = f(n-1) - newborn(n-9) 去年旧兔子数量=f(n−1)−newborn(n−9)

今年新出生兔子数量=newborn(n) 今年新出生兔子数量 = newborn(n) 今年新出生兔子数量=newborn(n)

故
KaTeX parse error: Unknown column alignment: * at position 24: … \begin{array}{*̲*lr**} f(n) = n…
f(n)代码实现如下:

int f(int n) {
    if(n <= 0) return 0;
    if(n == 1) return 1;
    if(n == 2) return 1;
    if(n = 10){
        return f(n-1) + newborn(n) - newborn(n-9);
    }
}

就剩下newborn(n)函数没有定义了，其实newborn数列也是一个斐波那契数列，如下表：

年份 n	新出生 newborn	公式 g(n)
1	`1`	g(1)=1
2	`0`	g(2) = 0
3	第一年的兔子生啦！`1`	g(3) = g(1) = g(1)+g(2)
4	第一年和第二年的兔子生啦！`1+0=1`	g(4) = g(1)+g(2) = g(3)+g(2)
5	一、二、三年的兔子都生啦！`1+0+1=2`	g(5) = g(1)+g(2)+g(3) = g(4)+g(3)
6	一到四年的兔子都生啦！`1+0+1+1=3`	g(6) = g(1)+g(2)+g(3)+g(4) = g(5)+g(4)
…	…	…

推出来了！又是一个斐波那契数列，公式如下：
newborn(n)=newborn(n−1)+newborn(n−2) newborn(n) = newborn(n-1)+newborn(n-2) newborn(n)=newborn(n−1)+newborn(n−2)
再加上上面的死亡条件：
KaTeX parse error: Unknown column alignment: * at position 24: … \begin{array}{*̲*lr**} newborn(…
newborn代码实现如下：

int newborn(int n){
    if(n <= 0) return 0;
    if(n == 1) return 1;
    if(n == 2) return 0;
    if(n = 10){
        return newborn(n-2) + newborn(n-1) - newborn(n-9);
    }
}

至此，兔子繁殖的问题已经解决完了，希望武汉疫情早日结束，大家能吃上美味的兔兔！武汉加油！中国加油！

作者：辉辉不是学霸

兔子

1024 个赞