Dijkstra与SPFA算法的不同之处对比
SPFA算法
此处为SPFA算法详解
用dis数组记录源点到有向图上任意一点距离,其中源点到自身距离为0,到其他点距离为
INF。将源点入队,并重复以下步骤:
1、队首x出队
2、遍历所有以队首为起点的有向边(x,i),若dis[x]+w(x,i)<dis[i],则更新dis[i]
3、如果点i不在队列中,则i入队
4、若队列为空,跳出循环;否则执行1
Dijkstra算法
此处为Dijkstra算法详解
清除所有点的标号;
设d[0]=0,其他d[i]=INF;//INF是一个很大的值,用来替代正无穷
循环n次 {
在所有未标号结点中,选出d值最小的结点x;
给结点x标记;
对于从x出发的所有边(x,y),更新d[y] = min{d[y], d[x]+w(x,y)}
二者最主要的区别在于:
SPFA算法可以处理带负权的边,而Dijkstra算法不行。
Dijkstra算法采用贪心策略,每次选择距当前最近的点进行延伸(贪心,不公平),但贪心往往只能求得局部最优解,如下图,用Dijkstra算法的话,显然1->2是当前的最短路径; SPFA算法类似于bfs,属于同一层次的结点都会遍历到(公平),它求得的的最短路径是1->3->2。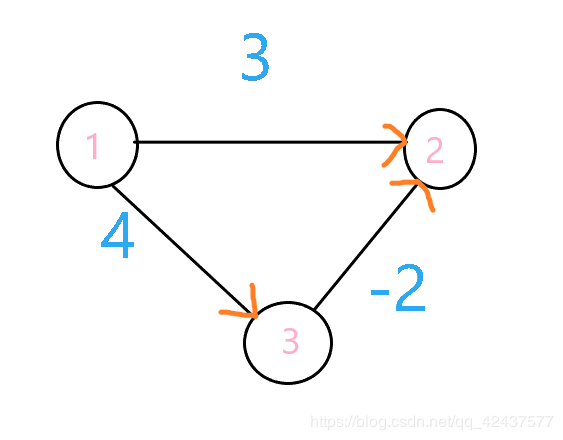

作者:波点兔