过拟合与欠拟合、梯度消失与爆炸、RNN进阶
专业名词解释:
泛化误差(generalization error):指模型在任意一个测试数据样本上表现出来的误差的期望,我们通常用测试集上的误差来近似看待.
验证集(validation set):预留一部分训练数据集出来用于验证和看模型的表现结果,并用来进行模型选择
K折交叉验证(K-fold cross-validation):针对训练数据不够用时的一种改善方法。把原始训练数据集分割成不重合的K份子数据集,然后做K次的训练和验证,最后对这K次的训练误差和验证误差分别求平均
欠拟合模型无法得到较低的训练误差,我们将这一现象称作欠拟合(underfitting)
过拟合模型的训练误差远小于它在测试数据集上的误差,我们称该现象为过拟合(overfitting)。
影响拟合问题的因素其实影响因素是非常多的,不过有两个比较重点,模型复杂度和训练集大小
模型复杂度模型过于复杂意味着权重参数很多,会使得模型考虑的细节越来越多,从而导致泛化能力就越来越差,下面是模型复杂度和误差的关系:

训练数据集中的样本数过少,会容易发生过拟合,而泛化误差并不会因为训练集的数量增加而增加,所以希望训练集越大越好,特别是当模型复杂度较高时。
应对过拟合的常用手段:权重衰减权重衰减等价于L2范数正则化,正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小,是应对过拟合的常用手段。
L2范数正则化:
即在原损失函数基础上添加L2范数惩罚项,L2 范数惩罚项指的是模型权重参数每个元素的平方和与一个正的常数的乘积,如下例子:
线性回归损失函数:
ℓ(w1,w2,b)=1n∑i=1n12(x1(i)w1+x2(i)w2+b−y(i))2\ell(w_1, w_2, b) = \frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right)^2ℓ(w1,w2,b)=n1i=1∑n21(x1(i)w1+x2(i)w2+b−y(i))2
正则化后:
ℓ(w1,w2,b)+λ2n∣w∣2\ell(w_1, w_2, b) + \frac{\lambda}{2n} |\boldsymbol{w}|^2ℓ(w1,w2,b)+2nλ∣w∣2
其中超参数λ>0\lambda > 0λ>0。当权重参数均为0时,惩罚项最小。当λ\lambdaλ较大时,惩罚项在损失函数中的比重较大,这通常会使学到的权重参数的元素较接近0。当λ\lambdaλ设为0时,惩罚项完全不起作用。上式中L2L_2L2范数平方∣w∣2|\boldsymbol{w}|^2∣w∣2展开后得到w12+w22w_1^2 + w_2^2w12+w22。
有了L2L_2L2范数惩罚项后,在小批量随机梯度下降中,我们将线性回归一节中权重w1w_1w1和w2w_2w2的迭代方式更改为
w1←(1−ηλ∣B∣)w1−η∣B∣∑i∈Bx1(i)(x1(i)w1+x2(i)w2+b−y(i)),w2←(1−ηλ∣B∣)w2−η∣B∣∑i∈Bx2(i)(x1(i)w1+x2(i)w2+b−y(i)). \begin{aligned} w_1 &\leftarrow \left(1- \frac{\eta\lambda}{|\mathcal{B}|} \right)w_1 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_1^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right),\\ w_2 &\leftarrow \left(1- \frac{\eta\lambda}{|\mathcal{B}|} \right)w_2 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_2^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right). \end{aligned} w1w2←(1−∣B∣ηλ)w1−∣B∣ηi∈B∑x1(i)(x1(i)w1+x2(i)w2+b−y(i)),←(1−∣B∣ηλ)w2−∣B∣ηi∈B∑x2(i)(x1(i)w1+x2(i)w2+b−y(i)).
可见,L2L_2L2范数正则化令权重w1w_1w1和w2w_2w2先自乘小于1的数,再减去不含惩罚项的梯度。因此,L2L_2L2范数正则化又叫权重衰减。权重衰减通过惩罚绝对值较大的模型参数为需要学习的模型增加了限制,这可能对过拟合有效。
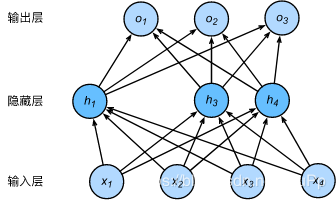
针对神经网络的正则化:丢弃法Dropout假设一个单隐藏层的多层感知机,输入个数为4,隐藏单元为5个,表达式如下:
hi=ϕ(x1w1i+x2w2i+x3w3i+x4w4i+bi)
h_i = \phi\left(x_1 w_{1i} + x_2 w_{2i} + x_3 w_{3i} + x_4 w_{4i} + b_i\right)
hi=ϕ(x1w1i+x2w2i+x3w3i+x4w4i+bi)
当对该隐藏层使用丢弃法时,该层的隐藏单元将有一定概率被丢弃掉。设丢弃概率为ppp,那么有ppp的概率hih_ihi会被清零,有1−p1-p1−p的概率hih_ihi会除以1−p1-p1−p做拉伸。丢弃概率是丢弃法的超参数。具体来说,设随机变量ξi\xi_iξi为0和1的概率分别为ppp和1−p1-p1−p。使用丢弃法时我们计算新的隐藏单元hi′h_i'hi′
hi′=ξi1−phi
h_i' = \frac{\xi_i}{1-p} h_i
hi′=1−pξihi
由于E(ξi)=1−pE(\xi_i) = 1-pE(ξi)=1−p,因此
E(hi′)=E(ξi)1−phi=hi
E(h_i') = \frac{E(\xi_i)}{1-p}h_i = h_i
E(hi′)=1−pE(ξi)hi=hi
即丢弃法不改变其输入的期望值。
期望值的科普:每次可能结果的概率乘以其结果的总和
E(X) = X1p(X1) + X2p(X2) + …… + Xn*p(Xn)
按照上面的例子,如果h2和h5被清零了,那么输出层不再依赖h2和h5,反向传播时这两个隐藏单元的相关权重的梯度为0。因为是随机的,所有隐藏单元都有机会被清零,那样输出层就无法过度依赖任意一个单元,从而达到正则化的作用
深度模型有关的数值稳定性的典型问题:梯度消失和梯度爆炸
当神经网络的层数较多时,模型的数值稳定性容易变差。
假设一个L层的多层感知机,且设所有隐藏层的激活函数为恒等映射(identity mapping) ϕ(x)=x 。给定输入X\boldsymbol{X}X,多层感知机的第lll层的输出H(l)=XW(1)W(2)…W(l)\boldsymbol{H}^{(l)} = \boldsymbol{X} \boldsymbol{W}^{(1)} \boldsymbol{W}^{(2)} \ldots \boldsymbol{W}^{(l)}H(l)=XW(1)W(2)…W(l)。如果层数较大就会出现衰减或者爆炸。
现在我们假设L=30,多层感知机的第30层输出为输入X\boldsymbol{X}X分别与0.230≈1×10−210.2^{30} \approx 1 \times 10^{-21}0.230≈1×10−21(消失)和530≈9×10205^{30} \approx 9 \times 10^{20}530≈9×1020(爆炸)的乘积。当层数较多时,梯度的计算也容易出现消失或爆炸。
在线性回归的简洁实现中,我们使用torch.nn.init.normal_()使模型net的权重参数采用正态分布的随机初始化方式。不过,PyTorch中nn.Module的模块参数都采取了较为合理的初始化策略(不同类型的layer具体采样的哪一种初始化方法的可参考源代码),因此一般不用我们考虑。
还有一种比较常用的随机初始化方法叫作Xavier随机初始化。
假设某全连接层的输入个数为aaa,输出个数为bbb,Xavier随机初始化将使该层中权重参数的每个元素都随机采样于均匀分布
U(−6a+b,6a+b). U\left(-\sqrt{\frac{6}{a+b}}, \sqrt{\frac{6}{a+b}}\right). U(−a+b6,a+b6).
它的设计主要考虑到,模型参数初始化后,每层输出的方差不该受该层输入个数影响,且每层梯度的方差也不该受该层输出个数影响。
考虑环境因素一、协变量偏移
虽然输入的分布可能随时间而改变,但是标记函数,即条件分布P(y∣x)不会改变。
例子:真实的猫狗图片训练,卡通的猫狗做测试.
问题根源是特征分布的变化(即协变量的变化),数学意义上的P(x)改变了,但P(y∣x)保持不变。
二、标签偏移
当我们认为导致偏移的是标签P(y)上的边缘分布的变化,但类条件分布是不变的P(x∣y)时,就会出现相反的问题。当我们认为y导致x时,标签偏移是一个合理的假设。例如,通常我们希望根据其表现来预测诊断结果。
病因(要预测的诊断结果)导致 症状(观察到的结果)。
训练数据集,数据很少只包含流感p(y)的样本。
而测试数据集有流感p(y)和流感q(y),其中不变的是流感症状p(x|y)。
有时标签偏移和协变量移位假设可以同时成立。
如果数据量足够的情况下,确保训练数据集和测试集中的数据取自同一个数据集,可以防止协变量偏移和标签偏移是正确的。如果数据量很少,少到测试集中存在训练集中未包含的标签,就会发生标签偏移。
三、概念偏移
标签的本身定义发生了变化,例子:软饮料
美国的不同地区对soft drink的理解有:soda、pop、coke
如果我们要建立一个机器翻译系统,分布P(y∣x)可能因我们的位置而异。这个问题很难发现。另一个可取之处是P(y∣x)通常只是逐渐变化。
回顾RNN的训练过程:
前向传播做预测 损失函数比较预测出来的值和真实值比较,输出一个loss值,loss可以判断模型的好坏程度 根据这个loss,进行根据时间步的反向传播,计算每个神经元的梯度 更新权重参数RNN具有短期记忆问题,会导致梯度爆炸和梯度消失,上一节使用了梯度裁剪来解决梯度爆炸问题,今天主要是关注梯度消失的问题,不过同时也可以缓解梯度爆炸,就是GRU和LSTM。
GRU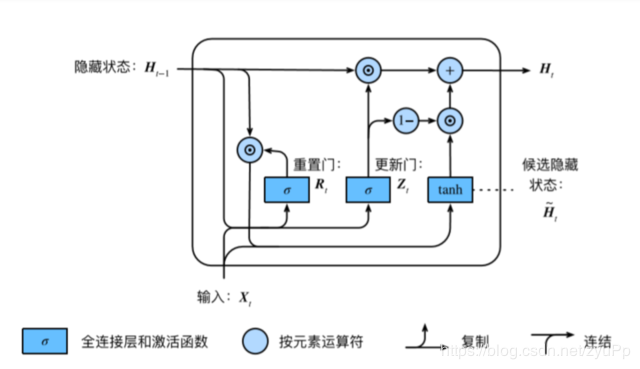
Rt=σ(XtWxr+Ht−1Whr+br)Zt=σ(XtWxz+Ht−1Whz+bz)H~t=tanh(XtWxh+(Rt⊙Ht−1)Whh+bh)Ht=Zt⊙Ht−1+(1−Zt)⊙H~t
R_{t} = σ(X_tW_{xr} + H_{t−1}W_{hr} + b_r)\\
Z_{t} = σ(X_tW_{xz} + H_{t−1}W_{hz} + b_z)\\
\widetilde{H}_t = tanh(X_tW_{xh} + (R_t ⊙H_{t−1})W_{hh} + b_h)\\
H_t = Z_t⊙H_{t−1} + (1−Z_t)⊙\widetilde{H}_t
Rt=σ(XtWxr+Ht−1Whr+br)Zt=σ(XtWxz+Ht−1Whz+bz)Ht=tanh(XtWxh+(Rt⊙Ht−1)Whh+bh)Ht=Zt⊙Ht−1+(1−Zt)⊙Ht
根据上面的图和公式,可以大概了解GRU的结构,主要就是比RNN多了两个门,重置门和更新门。
重置门:有助于捕捉时间序列的短期依赖关系 更新门:有助于捕捉时间序列的长期依赖关系初始化参数有12个:
重置门的参数:Wxr,Whr,brW_{xr} ,W_{hr} , b_rWxr,Whr,br
更新门的参数:Wxz,Whz,bzW_{xz},W_{hz}, b_zWxz,Whz,bz
候选隐藏状态参数:Wxh,Whh,bhW_{xh},W_{hh},b_hWxh,Whh,bh
第一个隐藏状态的初始化:torch.zeros((batch_size, num_hiddens), device=device)
输出层的参数:Whq,bqW_hq,b_qWhq,bq
长短期记忆long short term memory,作用和GRU相似,不过结构不一样
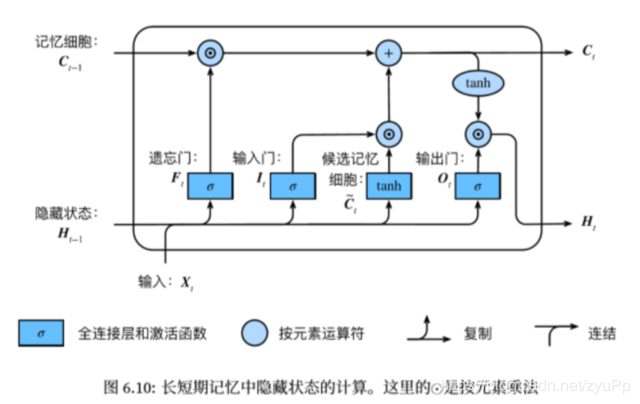
It=σ(XtWxi+Ht−1Whi+bi)Ft=σ(XtWxf+Ht−1Whf+bf)Ot=σ(XtWxo+Ht−1Who+bo)C~t=tanh(XtWxc+Ht−1Whc+bc)Ct=Ft⊙Ct−1+It⊙C~tHt=Ot⊙tanh(Ct)
I_t = σ(X_tW_{xi} + H_{t−1}W_{hi} + b_i) \\
F_t = σ(X_tW_{xf} + H_{t−1}W_{hf} + b_f)\\
O_t = σ(X_tW_{xo} + H_{t−1}W_{ho} + b_o)\\
\widetilde{C}_t = tanh(X_tW_{xc} + H_{t−1}W_{hc} + b_c)\\
C_t = F_t ⊙C_{t−1} + I_t ⊙\widetilde{C}_t\\
H_t = O_t⊙tanh(C_t)
It=σ(XtWxi+Ht−1Whi+bi)Ft=σ(XtWxf+Ht−1Whf+bf)Ot=σ(XtWxo+Ht−1Who+bo)Ct=tanh(XtWxc+Ht−1Whc+bc)Ct=Ft⊙Ct−1+It⊙CtHt=Ot⊙tanh(Ct)

Ht(1)=ϕ(XtWxh(1)+Ht−1(1)Whh(1)+bh(1))Ht(ℓ)=ϕ(Ht(ℓ−1)Wxh(ℓ)+Ht−1(ℓ)Whh(ℓ)+bh(ℓ))Ot=Ht(L)Whq+bq
\boldsymbol{H}_t^{(1)} = \phi(\boldsymbol{X}_t \boldsymbol{W}_{xh}^{(1)} + \boldsymbol{H}_{t-1}^{(1)} \boldsymbol{W}_{hh}^{(1)} + \boldsymbol{b}_h^{(1)})\\
\boldsymbol{H}_t^{(\ell)} = \phi(\boldsymbol{H}_t^{(\ell-1)} \boldsymbol{W}_{xh}^{(\ell)} + \boldsymbol{H}_{t-1}^{(\ell)} \boldsymbol{W}_{hh}^{(\ell)} + \boldsymbol{b}_h^{(\ell)})\\
\boldsymbol{O}_t = \boldsymbol{H}_t^{(L)} \boldsymbol{W}_{hq} + \boldsymbol{b}_q
Ht(1)=ϕ(XtWxh(1)+Ht−1(1)Whh(1)+bh(1))Ht(ℓ)=ϕ(Ht(ℓ−1)Wxh(ℓ)+Ht−1(ℓ)Whh(ℓ)+bh(ℓ))Ot=Ht(L)Whq+bq
我们一开始做RNN都是只有一层隐藏状态,从H1(1){H}_{1}^{(1)}H1(1)到HT(1){H}_{T}^{(1)}HT(1),然后输出O,但是深度的RNN,会把上一层的同一时刻的状态作为下一层的神经单元的输入X,然后计算,最后一层接上输出层。
双向循环神经网络在文本任务里能做到同时考虑上文和下文与当前词之间的依赖。。层数越深效果未必越好,层数的加深会导致模型的收敛变得困难
在实现深层上,只需要修改torch中num_layers参数即可
双向RNN
H→t=ϕ(XtWxh(f)+H→t−1Whh(f)+bh(f))H←t=ϕ(XtWxh(b)+H←t+1Whh(b)+bh(b))
\begin{aligned} \overrightarrow{\boldsymbol{H}}_t &= \phi(\boldsymbol{X}_t \boldsymbol{W}_{xh}^{(f)} + \overrightarrow{\boldsymbol{H}}_{t-1} \boldsymbol{W}_{hh}^{(f)} + \boldsymbol{b}_h^{(f)})\\
\overleftarrow{\boldsymbol{H}}_t &= \phi(\boldsymbol{X}_t \boldsymbol{W}_{xh}^{(b)} + \overleftarrow{\boldsymbol{H}}_{t+1} \boldsymbol{W}_{hh}^{(b)} + \boldsymbol{b}_h^{(b)}) \end{aligned} HtHt=ϕ(XtWxh(f)+Ht−1Whh(f)+bh(f))=ϕ(XtWxh(b)+Ht+1Whh(b)+bh(b))
Ht=(H→t,H←t)
\boldsymbol{H}_t=(\overrightarrow{\boldsymbol{H}}_{t}, \overleftarrow{\boldsymbol{H}}_t)
Ht=(Ht,Ht)
Ot=HtWhq+bq
\boldsymbol{O}_t = \boldsymbol{H}_t \boldsymbol{W}_{hq} + \boldsymbol{b}_q
Ot=HtWhq+bq
双向的循环神经网络的好处是:同时考虑了前面的字和后面的字,有助于更好地获得句子的信息。前向的HtH_tHt 和后向的HtH_tHt用concat进行连结
作者:zyuPp