洛谷P1002 过河卒题解
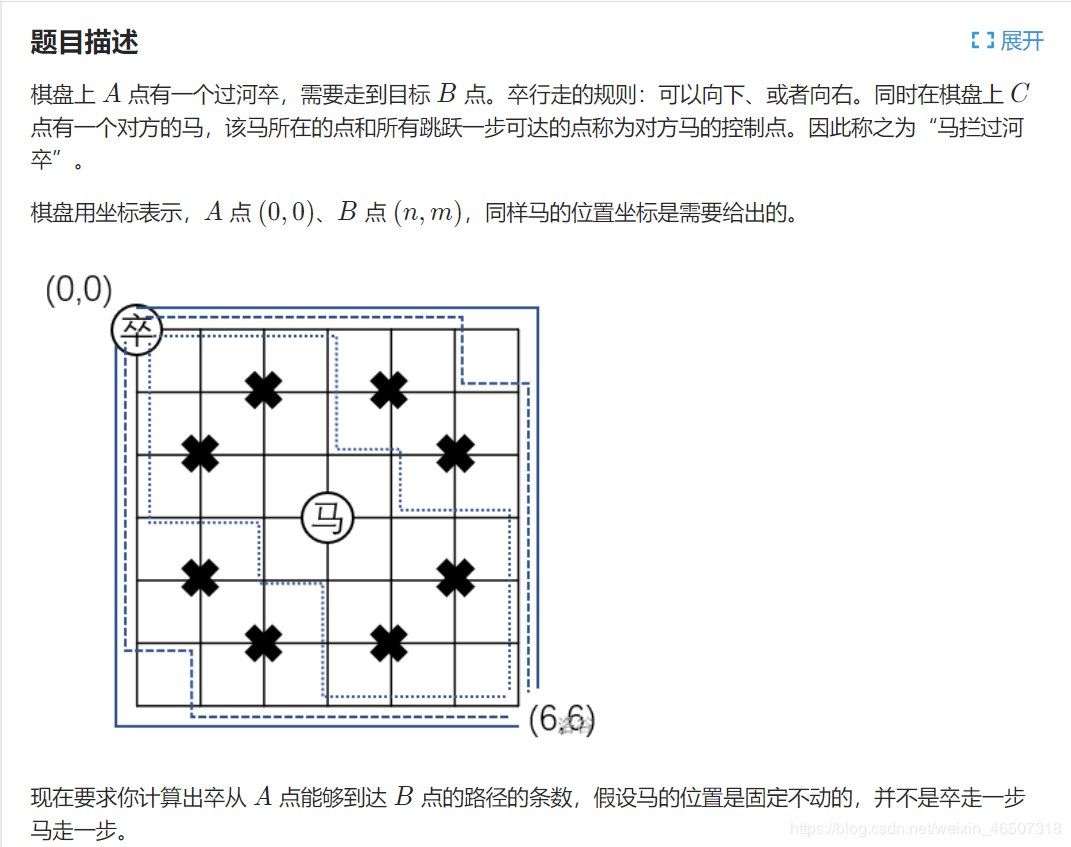
题意理解:在棋盘左上角标记为(0,0)的位置有卒,并使它走到指定位置,在棋盘另一指定位置有马,卒不能经过马以及马的控制点,求卒走到指定位置的走法总数?
解题思路:
1.把整个棋盘看成一个二维数组,首先判断马的控制点的个数,并把马以及马的控制点标记为-1.
2.马到达一个位置的总数等于马经过这一位置的左一格和上一个的和,如要马到达位置为(6,6),则走法总数等于马经过(5,6)和(6,5)的和,以此类推。
3.遍历整个二维数组,把数值等于-1的赋值为0,在边缘位置且不等于-1的赋值为1.其他位置的值为其左一格和上一格的和,目标位置的值即为卒的走法总数。
import java.util.Scanner;
public class Main {
public static long add(long[][] sum,int x,int y,int n,int m) {
//马的控制点最多为八个,若马在棋盘的边缘或靠近边缘位置,马的控制点会少于八个。
//判断马的控制点的个数以及把马和马的控制点标记为-1.
if(x>0) {
sum[x-1][y+2]=-1;
}
if(x>1 && y>0) {
sum[x-2][y-1]=-1;
}
if(x>0 && y>1) {
sum[x-1][y-2]=-1;
}
if(x>1) {
sum[x-2][y+1]=-1;
}
if(y>0) {
sum[x+2][y-1]=-1;
}
if(y>1) {
sum[x+1][y-2]=-1;
}
sum[x+1][y+2]=-1;
sum[x+2][y+1]=-1;
sum[x][y]=-1;
sum[0][0]=1;
//先对第一行进行赋值
for(int i=1;i<=n;i++) {
if(sum[i][0]==-1)
sum[i][0]=0;
else
sum[i][0]=sum[i-1][0];
}
//对第一列进行赋值
for(int i=1;i<=m;i++) {
if(sum[0][i]==-1)
sum[0][i]=0;
else
sum[0][i]=sum[0][i-1];
}
//遍历二维数组,进行赋值。
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
if(sum[i][j]==-1) {
sum[i][j]=0;
}
else
sum[i][j]=sum[i-1][j]+sum[i][j-1];
}
}
//目标位置的值即为卒的走法总数。
return sum[n][m];
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int[] arr = new int[2];
//卒的目标位置
int n=in.nextInt();
int m=in.nextInt();
//马的位置
for (int i = 0; i < 2; i++) {
arr[i] = in.nextInt();
}
//建立二维数组,可以适当取大,防止对马的控制点进行标记时角标越界。
long [][] sum=new long[n+3][m+3];
long s=add(sum,arr[0],arr[1],n,m);
System.out.println(s);
}
}
作者:foreverAC