牛客 MMset 树的点集直径(LCA)
链接:https://ac.nowcoder.com/acm/problem/14250
来源:牛客网
时间限制:C/C++ 3秒,其他语言6秒
空间限制:C/C++ 131072K,其他语言262144K
64bit IO Format: %lld
给定一棵n个节点的树,点编号为1…n。
Q次询问,每次询问给定一个点集S,令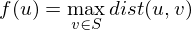 ,
,
你需要求出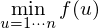 。
。
其中dist(u,v)表示树上路径(u,v)的边数。
输入描述:
第一行一个整数n,接下来n−1行每行两个整数表示树上的一条边。
接下来一行一个整数Q,接着Q行,每行第一个数是|S|,剩下|S|个互不相同的数代表这个集合。
输出描述:
输出Q行,每行一个整数表示答案。
题目大意大概就是上面的思路。
解析:
看了网上好多对于这个题目的思路 ,有虚树有LCA,但是虚树也是用LCA构建出来的所以...
但是呢 这题的关键,肯定是可以看出来的:求点集的直径。
关于树的直径有两种求法:
1.一种两次遍历:指定任意节点找到与该节点相距最远的点,然后从找到的点出发寻找最远的点,此时最远的点即为树的直径。
2.树形dp+启发式合并:从1开始每个节点进行合并即可。
对于点集来说,如果这题用虚数做的话 树形dp 是比较好用的,可惜我不会虚树。
看了一下网上的题解,用LCA做的都是这么写的:
找到点集中距离根节点最深的节点,然后从该节点开始运用LCA ,求得与其他点的距离取最大值。
其实这个方法的正确性来源于树的直径的第一种求法:可以反过来考虑,对于一个节点A,我们只要能找到一个点B,使得B到A的距离最远,那么就可以从A出发找一条最远的路线使之成为树的直径。很明显:对于深度最深的节点来言,我们总能找到一个点,使得该点到当前节点距离最远,很容易证明。因为两个节点要么在两个分支要么在同一条链上。
所以该复杂度就变成了nlgn,尽管Q次询问,当总的点集个数不超过1e6,所以可以解决:
AC:(LCA模板是自己的hhh)
/*** keep hungry and calm CoolGuang!***/
#pragma GCC optimize(2)
#include
#define debug(x) cout<<#x<<":"<<x<<endl;
using namespace std;
typedef long long ll;
typedef pair pp;
const ll INF=1e17;
const int maxn=1e6+18;
const int mod=1e9+7;
inline bool read(ll &num)
{char in;bool IsN=false;in=getchar();if(in==EOF) return false;while(in!='-'&&(in'9')) in=getchar();if(in=='-'){ IsN=true;num=0;}else num=in-'0';while(in=getchar(),in>='0'&&in<='9'){num*=10,num+=in-'0';}if(IsN) num=-num;return true;}
ll n,m,p;
struct node{
int e,next;
}edge[maxn];
ll cnt=0;
int head[maxn];
ll deep[maxn];//树的深度
int f[maxn][30];//fa[i][j] 节点i的2^j次方的祖先
void addedge(int u,int v){
edge[cnt]=node{v,head[u]};
head[u]=cnt++;
}
void dfs(int u,int fa)//预处理深度 与祖先的关系
{
deep[u]=deep[fa]+1;
f[u][0]=fa;
for(int i=1;(1<<i)<=deep[u];i++)//不加限制也行
f[u][i]=f[f[u][i-1]][i-1];//2^i = 2^(i-1)+2^(i-1)
for(int i=head[u];~i;i=edge[i].next){
int e=edge[i].e;
if(e!=fa) dfs(e,u);
}
}
int LCA(int u,int v)
{
if(deep[u]=0;i--) if(deep[f[u][i]]>=deep[v]) u=f[u][i];//比他深往上跳
if(u==v) return u;
for(int i=25;i>=0;i--){
if(f[u][i]!=f[v][i]){//因为从同一深度开始向上跳 一样有可能是更远的祖先
u=f[u][i];
v=f[v][i];
}
}
return f[u][0];//随便返回一个上一级即可
}
ll save[maxn];
int main()
{
memset(head,-1,sizeof(head));
read(n);
for(int i=1;i<=n-1;i++){
ll x,y;
read(x);read(y);
addedge(x,y);
addedge(y,x);
}
dfs(1,1);
read(m);
for(int i=1;i<=m;i++){
read(p);
ll maxx=0;
int u;
for(int k=1;kmaxx){
maxx=deep[save[k]];
u=save[k];
}
}
ll maxl=0;
for(int k=1;k<=p;k++){
int z=LCA(u,save[k]);
maxl=max(maxl,deep[u]+deep[save[k]]-2*deep[z]);
}
printf("%lld\n",(maxl+1)/2);
}
return 0;
}
/**
7 2 1
2 5
3 7
**/
作者:一只酷酷光儿( CoolGuang)