[TJOI2013]松鼠聚会【切比雪夫距离转换曼哈顿距离】

  首先，愚人节那天，暴力斩获30分，（暴力法真好用！

  然后，讲一下解题的思路吧，主要是怎样转换切比雪夫距离这里要有神奇的方法。

首先，我们先列举一下两点间切比雪夫距离的求解公式：

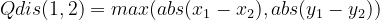
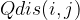指的是i、j两点的切比雪夫距离

于是，我们再用一些数学上的思维来拆解这个等式关系

这样的做法，是为了我们去掉最大值max()符号

之后，我们发现，似乎变成了新的坐标，我们移项来看

我的天呐，神不神奇？

等式右边，不就是曼哈顿距离了嘛。

只是原来的做了这样的转换

好神奇！！！

那么，原来的问题，就变成了如何求解各点到其余所有点的距离和了，二维偏序基础！

解决二维偏序问题，我们首先对第一维进行排序，就对x进行升序排序吧，然后就可以O(1)的求解其中一维了（x坐标）。

然后，利用树状数组+离散化的操作，我们处理第二维。

这样的处理方法是为了去掉绝对值，变成绝对大减去绝对小这样的形式了。

当然，主席树等数据结构，也是可以用以维护的。