逻辑回归（LR）公式推导及代码实现

文章目录构造hypothesis构造损失函数通过“梯度下降法”求参数 θ\thetaθ 的更新式代码实现References
逻辑回归是用来解决分类问题用的，与线性回归不同的是，逻辑回归输出的不是具体的值，而是一个概率。除去了sigmoid函数的逻辑归回和线性回归几乎是一样的。 构造hypothesis

逻辑回归的HHH可以看做是一个线性回归方程的结果经过一个sigmoid函数得到的结果（为正样本的概率），逻辑回归的假设函数如下：
hθ(x)=g(θTx)=11+e−θTx h _ { \theta } ( x ) = g \left( \theta ^ { T } x \right) = \frac { 1 } { 1 + e ^ { - \theta ^ { T } x } } hθ​(x)=g(θTx)=1+e−θTx1​

函数 hθ(x)h _ { \theta } ( x )hθ​(x) 表示样本被预测为正例 111 的概率，我们很容易的得到样本被预测为正例和负例的概率如下：
P(y=1∣x; θ)=hθ(x)P(y=0∣x; θ)=1−hθ(x) \begin{array} { l } P ( y = 1 | x ;\ \theta ) = h_{\theta} ( x ) \\ P ( y = 0 | x ; \ \theta ) = 1 - h _ { \theta } ( x ) \end{array} P(y=1∣x; θ)=hθ​(x)P(y=0∣x; θ)=1−hθ​(x)​

上式可以合并为一个式子：（预测结果的概率表示）
P(y∣x;θ)=(hθ(x))y(1−hθ(x))1−y P ( y | x ; \theta ) = \left( h _ { \theta } ( x ) \right) ^ { y } \left( 1 - h _ { \theta } ( x ) \right) ^ { 1 - y } P(y∣x;θ)=(hθ​(x))y(1−hθ​(x))1−y

构造损失函数

我们对“预测结果的概率表示”取似然函数，取似然函数就是将模型对样本的概率预测值累乘起来。得到如下的似然函数：
L(θ)=∏i=1mP(y(i)∣x(i);θ)=∏i=1m(hθ(x(i)))y(i)(1−hθ(x(i)))1−y(i) L ( \theta ) = \prod _ { i = 1 } ^ { m } P \left( y ^ { ( i ) } | x ^ { ( i ) } ; \theta \right) = \prod _ { i = 1 } ^ { m } \left( h _ { \theta } \left( x ^ { ( i ) } \right) \right) ^ { y ^ { ( i ) } } \left( 1 - h _ { \theta } \left( x ^ { ( i ) } \right) \right) ^ { 1 - y ^ { ( i ) } } L(θ)=i=1∏m​P(y(i)∣x(i);θ)=i=1∏m​(hθ​(x(i)))y(i)(1−hθ​(x(i)))1−y(i)

由于该式比较麻烦涉及连乘法，所以我们对其去加对数操作得到对数似然函数：

上述利用的是最大似然估计原理：极大似然估计就是利用已知的样本分布，找到最有可能（即最大概率）导致这种分布的参数值；或者说什么样的参数才能使我们观测到目前这组数据的概率最大。
l(θ)=log⁡L(θ)=∑i=1m(y(i)log⁡hθ(x(i))+(1−y(i))log⁡(1−hθ(x(i)))) l ( \theta ) = \log L ( \theta ) = \sum _ { i = 1 } ^ { m } \left( y ^ { ( i ) } \log h _ { \theta } \left( x ^ { ( i ) } \right) + \left( 1 - y ^ { ( i ) } \right) \log \left( 1 - h _ { \theta } \left( x ^ { ( i ) } \right) \right) \right) l(θ)=logL(θ)=i=1∑m​(y(i)loghθ​(x(i))+(1−y(i))log(1−hθ​(x(i))))

当似然函数求得最大值时，模型参数能够最大可能的满足当前的样本，求最大值使用梯度向上法，我们可以对似然函数加个负号，通过求等价问题的最小值来求原问题的最大值，这样我们就可以使用极大似然估计法。（注意这里还多加了个1m\frac { 1 } { m }m1​）
J(θ)=−1ml(θ) J ( \theta ) = - \frac { 1 } { m } l ( \theta ) J(θ)=−m1​l(θ)

这样我们就能得到损失函数的最终形式：
J(θ)=−1m∑i=1m(y(i)log⁡hθ(x(i))+(1−y(i))log⁡(1−hθ(x(i)))) J ( \theta ) = - \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \left( y ^ { ( i ) } \log h _ { \theta } \left( x ^ { ( i ) } \right) + \left( 1 - y ^ { ( i ) } \right) \log \left( 1 - h _ { \theta } \left( x ^ { ( i ) } \right) \right) \right) J(θ)=−m1​i=1∑m​(y(i)loghθ​(x(i))+(1−y(i))log(1−hθ​(x(i))))

即等价于：
cost⁡(hθ(x), y)={−log⁡(hθ(x)) if y=1−log⁡(1−hθ(x)) if y=0 \operatorname { cost } ( h _ { \theta } ( x ) ,\ y ) = \left\{ \begin{array} { l l } - \log \left( h _ { \theta } ( x ) \right) & \text { if } y = 1 \\ - \log \left( 1 - h _ { \theta } ( x ) \right) & \text { if } y = 0 \end{array} \right. cost(hθ​(x), y)={−log(hθ​(x))−log(1−hθ​(x))​ if y=1 if y=0​

通过“梯度下降法”求参数 θ\thetaθ 的更新式

我们下图为推导式，面试推导的时候可以不写下标（假设我们使用随机梯度下降法），这样可以使推导式更简洁。

求梯度：

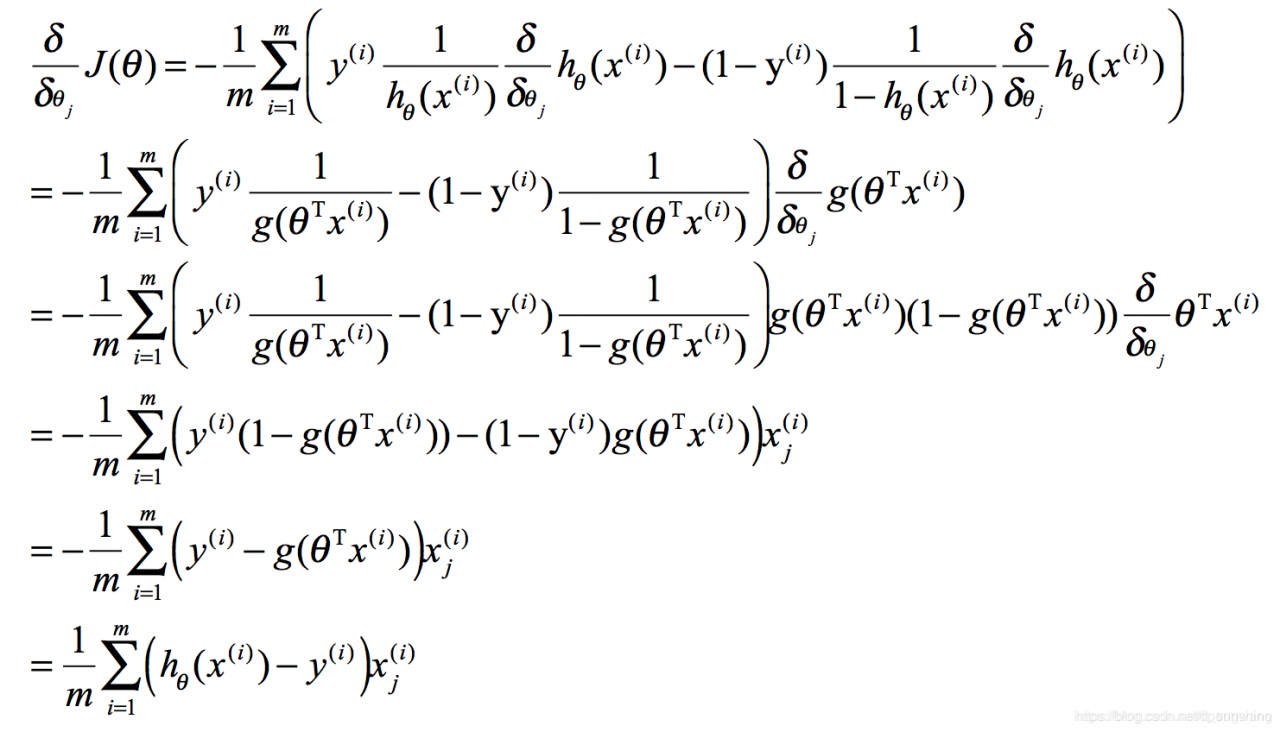
这里需要提一下的是，sigmoid函数有如下性质，在上述推导的第三行中可以看到：
S′(x)=e−x(1+e−x)2=S(x)(1−S(x)) S ^ { \prime } ( x ) = \frac { e ^ { - x } } { \left( 1 + e ^ { - x } \right) ^ { 2 } } = S ( x ) ( 1 - S ( x ) ) S′(x)=(1+e−x)2e−x​=S(x)(1−S(x))

θ更新式：α 为学习率
θj:=θj−α1m∑i=1m(hθ(x(i))−y(i))xj(i) \theta _ { j } : = \theta _ { j } - \alpha \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \left( h _ { \theta } \left( x ^ { ( i ) } \right) - y ^ { ( i ) } \right) x _ { j } ^ { ( i ) } θj​:=θj​−αm1​i=1∑m​(hθ​(x(i))−y(i))xj(i)​

总结：LR在确定了模型的形式后，通过最大似然估计法来实现最小散度从而求出模型参数。

代码实现

向量化：向量化是使用矩阵计算来代替for循环，以简化计算过程，提高效率。

# -*- coding: utf-8 -*- from numpy import * from matplotlib import pyplot as plt def plot_best_fit(wei, data_set, label): weights = wei data_set = array(data_set) n = shape(data_set)[0] xcourd1 = []; ycourd1 = [] xcourd2 = []; ycourd2 = [] for i in range(n): if int(label[i]) == 1: xcourd1.append(data_set[i, 1]); ycourd1.append(data_set[i, 2]) else: xcourd2.append(data_set[i, 1]); ycourd2.append(data_set[i, 2]) fig = plt.figure() ax = fig.add_subplot(111) ax.scatter(xcourd1, ycourd1, s=30, c='red', marker='s') ax.scatter(xcourd2, ycourd2, s=30, c='green') x = arange(-3.0, 3.0, 0.1) y = (-weights[0] - weights[1]*x)/weights[2] ax.plot(x, y) plt.xlabel('X1'); plt.ylabel('X2') plt.show() def load_data(): data_set = [] label = [] fr = open('./text.txt') for line in fr.readlines(): line = line.strip().split() data_set.append([1.0, float(line[0]), float(line[1])]) label.append(int(line[2])) return data_set, label def sigmoid(x): return 1.0 / (1 + exp(-x)) # 梯度下降算法 GD def train(data_set, label): data_matrix = mat(data_set) label = mat(label).transpose() m, n = shape(data_matrix) alpha = 0.001 max_cycles = 500 weights = ones((n, 1)) for k in range(max_cycles): h = sigmoid(data_matrix*weights) error = h - label weights = weights - alpha * data_matrix.transpose() * error return weights # on line to study SGD def stoc_grad_descent(data_set, label): m, n = shape(data_set) alpha = 0.01 weights = ones(n) for i in range(m): h = sigmoid(sum(data_set[i]*weights)) error = h - label[i] weights = weights - alpha * error * data_set[i] return weights # on line to study prove def prove_grad_ascent(data_set, label, num_iter=450): m, n = shape(data_set) weights = ones(n) for j in range(num_iter): data_index = range(m) for i in range(m): alpha = 4/(1.0+j+i)+0.01 # prevent swings # choose a random value to prevent periodic swings rand_index = int(random.uniform(0, len(data_index))) h = sigmoid(sum(data_set[rand_index]*weights)) error = label[rand_index] - h weights = weights + alpha * error * data_set[rand_index] del data_index[rand_index] return weights if __name__ == "__main__": data_set, label = load_data() #print label #weights = train(array(data_set), label) #weights = stoc_grad_ascent(array(data_set), label) weights = prove_grad_ascent(array(data_set), label) plot_best_fit(weights, data_set, label) References https://blog.csdn.net/dpengwang/article/details/86746233 https://www.jianshu.com/p/471b2fd570a3
作者：aift

lr 逻辑回归 回归