逻辑回归(Logistics Regression)
线性回归处理的因变量都是数值型区间变量,建立的模型描述的是因变量的期望与自变量之间的线性关系:hθ(x)=θ0x0+θ1x1+…+θnxnh_θ(x)=θ_0x_0+θ_1x_1+…+θ_nx_nhθ(x)=θ0x0+θ1x1+…+θnxn。
而在采用回归模型分析实际问题中,所研究的变量往往不全是区间变量而是顺序变量或属性变量,比如二项分布问题。通过分析年龄、性别、体质指数、平均血压等指标,判断一个人是否患有糖尿病,Y=0Y=0Y=0表示未患病,Y=1Y=1Y=1表示患病,这里的响应变量是一个两点(0-1)分布变量,它就不能用函数连续的值来预测因变量YYY了。
总之,线性回归模型通常是处理因变量是连续变量的问题,如果因变量是定性变量,线性回归模型就不再适用了,需采用逻辑回归模型解决。
逻辑回归(Logistics Regression)是用于处理因变量为分类变量的回归问题,常见的是二分类或者二项分布,也可以处理多分类问题,实际是一种分类方法。
1、sigmoid函数
逻辑回归虽然名字带有“回归”,但是它实际是一种分类方法,用于二分类问题(即输出只有两种)。在这里,我们需要找到一个预测函数hhh,显然,该函数的输出必须是两个值(分别代表两个类别)。
所以,在这里我们采用了sigmoid函数。
sigmoid函数的表达式:g(z)=11+e−zg(z)=\frac{1}{1+e^{-z}}g(z)=1+e−z1,函数图像如下图所示:
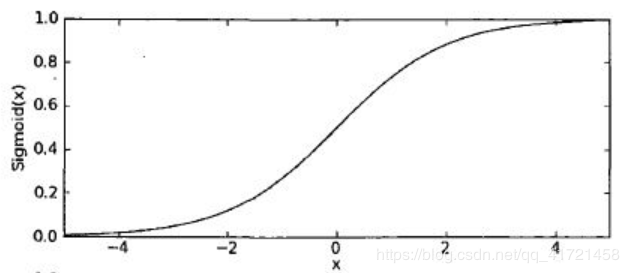
二分类问题的概率与自变量之间的关系往往是一种SSS型曲线,如下图所示,采用sigmoid函数实现:
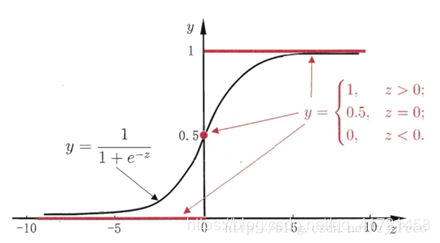
解释:将任意的输入映射到了[0,1][0,1][0,1]区间,我们在线性回归中可以得到一个预测值,再将该值映射到sigmoid函数中,这样就完成了由值到概率的转换,也就是分类任务。
2、推导
预测函数:hθ(x)=g(θTx)=11+e−θTxh_θ(x)=g(θ^Tx)=\frac{1}{1+e^{-θ^Tx}}hθ(x)=g(θTx)=1+e−θTx1
其中,θ0x0+θ1x1+…+θnxn=∑i−0nθixi=θTxθ_0x_0+θ_1x_1+…+θ_nx_n=\sum\limits_{i-0}^nθ_ix_i=θ^Txθ0x0+θ1x1+…+θnxn=i−0∑nθixi=θTx。
分类任务的概率为:{P(y=1∣x;θ)=hθ(x)P(y=0∣x;θ)=1−hθ(x)\begin{cases}P(y=1|x;θ)=h_θ(x) &\\P(y=0|x;θ)=1-h_θ(x) \end{cases}{P(y=1∣x;θ)=hθ(x)P(y=0∣x;θ)=1−hθ(x)
整合一下变为:P(y∣x;θ)=(hθ(x))y(1−hθ(x))1−yP(y|x;θ)=(h_θ(x))^y(1-h_θ(x))^{1-y}P(y∣x;θ)=(hθ(x))y(1−hθ(x))1−y
解释:对于二分类任务(0-1),整合后yyy取0时,只保留(1−hθ(x))1−y(1-h_θ(x))^{1-y}(1−hθ(x))1−y,yyy取1时,只保留(hθ(x))y(h_θ(x))^y(hθ(x))y。
接下来,我们将上述概率转换为似然函数和对数似然:
似然函数:L(θ)=∏i=1mP(yi∣xi;θ)=∏i=1m(hθ(xi))yi(1−hθ(xi))1−yiL(θ)=\prod\limits_{i=1}^mP(y_i|x_i;θ)=\prod\limits_{i=1}^m(h_θ(x_i))^{y_i}(1-h_θ(x_i))^{1-y_i}L(θ)=i=1∏mP(yi∣xi;θ)=i=1∏m(hθ(xi))yi(1−hθ(xi))1−yi
对数似然:l(θ)=logL(θ)=∑i=1m(yiloghθ(xi)+(1−yi)log(1−hθ(xi)))l(θ)=logL(θ)=\sum\limits_{i=1}^m(y_ilogh_θ(x_i)+(1-y_i)log(1-h_θ(x_i)))l(θ)=logL(θ)=i=1∑m(yiloghθ(xi)+(1−yi)log(1−hθ(xi)))
注:统计学中,似然函数是一种关于统计模型参数的函数。给定输出xxx时,关于参数θθθ的似然函数L(θ∣x)L(θ|x)L(θ∣x)(在数值上)等于给定参数θθθ后变量XXX的概率:L(θ∣x)=P(X=x∣θ)L(θ|x)=P(X=x|θ)L(θ∣x)=P(X=x∣θ)
引入我们的损失函数:J(θ)=−1ml(θ)J(θ)=-\frac{1}{m}l(θ)J(θ)=−m1l(θ),从而转换为梯度下降任务。
损失函数的求导过程:
J(θ)=−1m∑i=1m(yiloghθ(xi)+(1−yi)log(1−hθ(xi)))J(θ)=-\frac{1}{m}\sum\limits_{i=1}^m(y_ilogh_θ(x_i)+(1-y_i)log(1-h_θ(x_i)))J(θ)=−m1i=1∑m(yiloghθ(xi)+(1−yi)log(1−hθ(xi)))
∂∂θjJ(θ)=−1m∑i=1m(yi1hθ(xi))∂∂θjhθ(xi)−(1−yi)11−hθ(xi)∂∂θjhθ(xi))=−1m∑i=1m(yi1g(θTxi)−(1−yi)11−g(θTxi))∂∂θjg(θTxi)=−1m∑i=1m(yi1g(θTxi)−(1−yi)11−g(θTxi))g(θTxi)(1−g(θTxi))∂∂θjθTxi=−1m∑i=1m(yi(1−g(θTxi))−(1−yi)g(θTxi))xij=−1m∑i=1m(yi−g(θTxi))xij=1m∑i=1m(hθ(xi)−yi)xij\begin{aligned}
\frac{∂}{∂_{θ_j}}J(θ) & = -\frac{1}{m}\sum\limits_{i=1}^m(y_i\frac{1}{h_θ(x_i)})\frac{∂}{∂_{θ_j}}h_θ(x_i)-(1-y_i)\frac{1}{1-h_θ(x_i)}\frac{∂}{∂_{θ_j}}h_θ(x_i)) \\
& =-\frac{1}{m}\sum\limits_{i=1}^m(y_i\frac{1}{g(θ^Tx_i)}-(1-y_i)\frac{1}{1-g(θ^Tx_i)})\frac{∂}{∂_{θ_j}}g(θ^Tx_i) \\
& = -\frac{1}{m}\sum\limits_{i=1}^m(y_i\frac{1}{g(θ^Tx_i)}-(1-y_i)\frac{1}{1-g(θ^Tx_i)})g(θ^Tx_i)(1-g(θ^Tx_i))\frac{∂}{∂_{θ_j}}θ^Tx_i \\
& =-\frac{1}{m}\sum\limits_{i=1}^m(y_i(1-g(θ^Tx_i))-(1-y_i)g(θ^Tx_i))x_i^j \\
& =-\frac{1}{m}\sum\limits_{i=1}^m(y_i-g(θ^Tx_i))x_i^j \\
& = \frac{1}{m}\sum\limits_{i=1}^m(h_θ(x_i)-y_i)x_i^j
\end{aligned}∂θj∂J(θ)=−m1i=1∑m(yihθ(xi)1)∂θj∂hθ(xi)−(1−yi)1−hθ(xi)1∂θj∂hθ(xi))=−m1i=1∑m(yig(θTxi)1−(1−yi)1−g(θTxi)1)∂θj∂g(θTxi)=−m1i=1∑m(yig(θTxi)1−(1−yi)1−g(θTxi)1)g(θTxi)(1−g(θTxi))∂θj∂θTxi=−m1i=1∑m(yi(1−g(θTxi))−(1−yi)g(θTxi))xij=−m1i=1∑m(yi−g(θTxi))xij=m1i=1∑m(hθ(xi)−yi)xij
参数更新:
使用梯度下降的方法对参数进行更新。
θj:=θj−α1m∑i=1m(hθ(xi)−yi)xijθ_j:=θ_j-α\frac{1}{m}\sum\limits_{i=1}^m(h_θ(x_i)-y_i)x_i^jθj:=θj−αm1i=1∑m(hθ(xi)−yi)xij
注:参数每更新一次,说明朝着优化的方向前进了一步(参数的改变导致线性回归的值的改变,从而使得概率改变)。
多分类的softmaxsoftmaxsoftmax:
hθ(x(i))=[p(yi)=1∣x(i);θp(yi)=2∣x(i);θ⋮p(yi)=k∣x(i);θ]=1∑j=1keθjTx(i)[eθ1Tx(i)eθ2Tx(i)⋮eθkTx(i)]h_θ(x^{(i)})=\begin{bmatrix}p(y_i)=1|x^{(i)};θ\\p(y_i)=2|x^{(i)};θ\\\vdots \\ p(y_i)=k|x^{(i)};θ\end{bmatrix}=\frac{1}{\sum\limits_{j=1}^ke^{θ_j^Tx^{(i)}}}\begin{bmatrix}e^{θ_1^Tx^{(i)}}\\e^{θ_2^Tx^{(i)}}\\\vdots \\ e^{θ_k^Tx^{(i)}}\end{bmatrix}hθ(x(i))=⎣⎢⎢⎢⎡p(yi)=1∣x(i);θp(yi)=2∣x(i);θ⋮p(yi)=k∣x(i);θ⎦⎥⎥⎥⎤=j=1∑keθjTx(i)1⎣⎢⎢⎢⎢⎡eθ1Tx(i)eθ2Tx(i)⋮eθkTx(i)⎦⎥⎥⎥⎥⎤
作者:somnus丶夜小贱