详解kmp算法，简单易理解

Ester ·

更新时间:2024-09-21

· 555 次阅读

kmp算法简介

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)。

简单来说：

kmp算法，利用模式串的最长的相同的前后缀进行移动，而主串不需要回溯，从而达到快速匹配的目的。

举个例子：

如下图，在箭头处发生不匹配时，找到箭头之前模式串子串的最长的相同的前后缀，为AB；
在这里插入图片描述
然后把前缀AB移动到后缀AB的位置；

再继续进行匹配，同理，发生不匹配时，找到箭头之前模式串子串的最长的相同的前后缀，为A；

然后把前缀A移动到后缀A的位置，因为超出主串长度所以匹配失败。
在这里插入图片描述

再举个例子：

如下图，在箭头处发生不匹配时，找到箭头之前模式串子串的最长的相同的前后缀，为ABA；
在这里插入图片描述
然后把前缀ABA移动到后缀ABA的位置；

再继续进行匹配，同理，发生不匹配时，找到箭头之前模式串子串的最长的相同的前后缀，为A；

然后把前缀A移动到后缀A的位置，继续匹配，匹配成功。

求得next数组

设模式串为p，要注意的是模式串索引是从0到p.size()-1,而next数组与之对应的是1到p.size()，next[0]=-1。

void getNext(string p, int *next)
{
	next[0]=-1;
	int i=0,j=-1;//j是前缀，y是后缀
	while (i<p.size())
	{
		if(j==-1||p[i]==p[j])
		{
			++i;
			++j;
			next[i]=j;
		}
		else
		{
			j=next[j];//回溯
		}
	}
}

最难理解的就是这句,

		j=next[j];//回溯

为什么是这样呢？别急，举个例子：
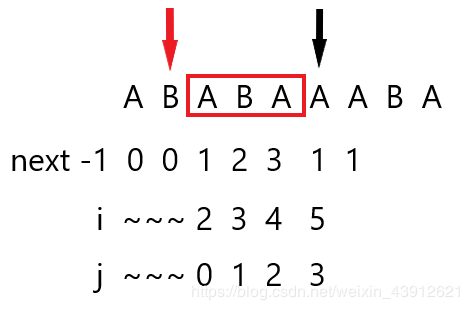
在这里插入图片描述
当i=5,j=3时，即黑箭头位置，p[i]!=p[j]，i和j的索引从0到p.size()，然后j=next[j]，即j=1，也就是红箭头的位置,不相等继续回溯到j=0，这样回溯就节省了时间。可回溯的原因是前缀是已知的，我们的next数组中存储了每个索引的最长的相等的前后缀。

C++实现：

#include
using namespace std;
void getNext(string p, int *next)
{
	next[0]=-1;
	int i=0,j=-1;
	while (i<p.size())
	{
		if(j==-1||p[i]==p[j])
		{
			++i;
			++j;
			next[i]=j;
		}
		else
		{
			j=next[j];
		}
	}
	for(int i=0;i<=p.size();i++)
	{
		cout<<next[i]<>x>>y;
	getNext(y,next);
	int ans=kmp(x,y,next);
	cout<<ans;
	return 0;
}

作者：fakerth

kmp算法 kmp

1024 个赞