kmp-学习理解记录
本片是在回忆kmp的时候写下的,最近老师再讲这个,又发现之前写的都忘的差不多了在这里从新写一下笔记,纯小白文字:
基础暴力:再看kmp的时候我们先来讲讲常规的模式串的暴力匹配,对于常规的一个文本串S以及一个匹配的字串P,最简单的想法就是两个指针,从S和P的头开始匹配,两个指针i,j同时开始出发,然后当i和P的第一个字符匹配的时候然后i,j同时递增,当j走到P的最后,字符串的匹配就完成了,但是如果中间某一段不匹配了就需要回到第一个匹配到P的首字母的i的位置,光打字可能有点难以理解,所以还是拿图说话,这里假设S的字符串为easdkjfassdfwe,然后需要匹配的模式串P为ass。
ok,第一步,i和j默认都是从队列首开始

第二步,明显e和a不匹配,所以i要加1

第三步,a和a匹配上了,所以这个时候,i和j同时向后走

第四步,i位和j位的s又匹配上了,所以i和j继续往后移一位

第五步,i位置和j位,d和s不匹配,所以i需要往后退j-1个位置,然后j重置为最前面的位置

第六步,然后重复上面的过程,直到匹配到了下一个和j位的a的位置,如下

第七步,还是当匹配到了头之后,i和j一起往后走


知道最后,j=模式串P的长度-1的时候,说明匹配完成了,就能得出结论,匹配成功了,但是其实算法还是可以有优化的,当前这个模式串可能看不出来,但是如果把文本串换成abcabcabe,模式串换成abe,那每次回到头的操作其实就是损失了大量的效率,在文本串模式串都比较短的情况下,优化的效果可能没有那么明显,但是一旦数量变大了之后,时间优化是很明显的,所以这就是下面要回忆的kmp算法
kmp算法这个算法里最重要是一部步骤就是,你要怎么确定,在回溯的时候,往回跳几个位置,而不是每次都是回退j-1的位置,这里就涉及到一个部分匹配表(Partial Match Table),他会在你每次匹配部分的时候,根据已知的信息来告诉你i应该往后退几位是最快的,涉及到部分匹配的时候,这里又要提到一个新的概念,前缀和后缀,"前缀"指除了最后一个字符以外,一个字符串的全部头部组合;"后缀"指除了第一个字符以外,一个字符串的全部尾部组合。这么说可能有点干吧,还是上图,我们假设需要匹配的模式串为qwerqw,然后我们需要求出他的部分匹配表

我们可以看到q的前缀和后缀都是空的所以q的值便是0,然后就qw,由于qw前缀只有一个w后缀只有一个q所以w下面的值依旧是0

接下来是qwe,也可以看到完全没有相同的前缀和后缀所以依旧是0
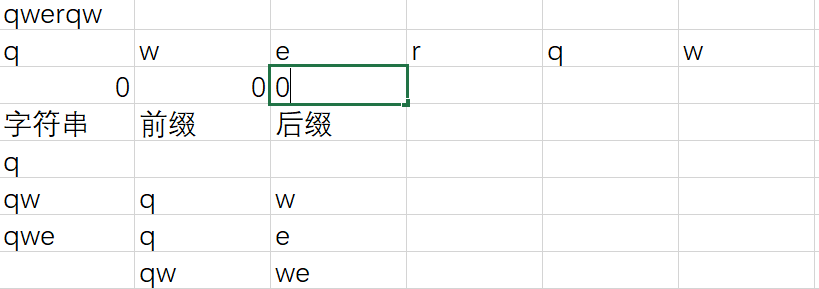
接下来是qwer
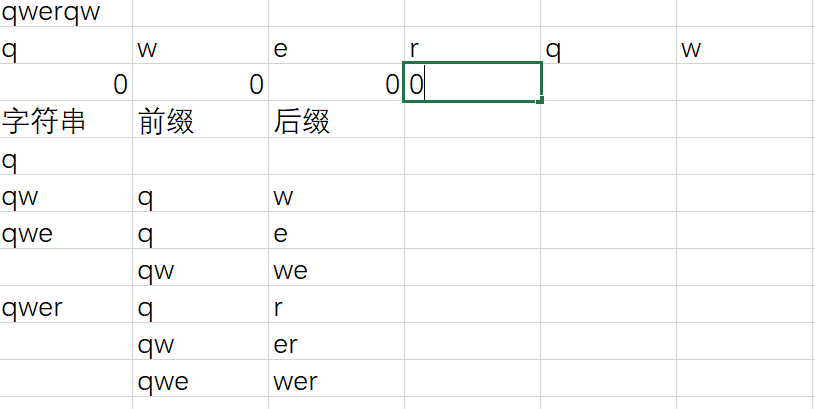
然后是qwerq,我们也可以看到有两个q相同了,所以q的位置为1

最后是qwerqw,
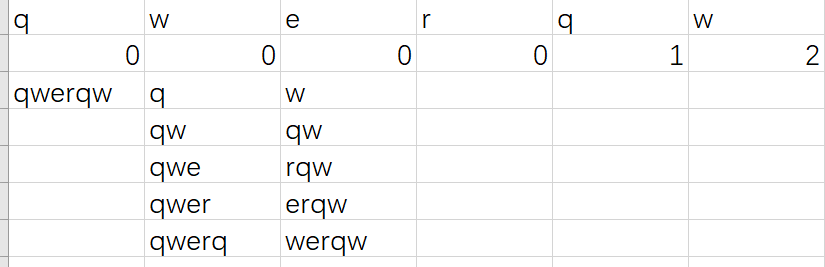
所以整个部分匹配表就得到了,下面是python的写法
把他打包成一个函数了,接受的参数是一个字符串返回是一个数组
def back_next(string):
back_next = [0 for i in range(len(s))]#创建一个结果数组
for i in range(len(s)): #循环字符串
tep = 0#把将要填入结果的匹配字符串长度初始化
if i==0:#如果是第一个直接返回
continue
for j in range(i):#切割字符串,每次拿前面j个和后面j个比较
t = s[:i+1]#创建一个临时数组来存放每次需要判断的字符串
if t[:j+1]==t[len(t)-j-1:]:#如果前i+1个和后i+1个相同,则把长度填入结果中
tep = j+1
back_next[i]=tep
return back_next
核心讲完了,然后就是怎么使用的方法了匹配的结果无非就是三种情况,第一种i位置和j位置的一直不相等,那这没啥好说了就是i递增就完事,第二种:i位置和j位置相等,那就是i和j同时递增这也简单,第三个就是,i位置和j位置前半部分相等,后半部分不相等,这个时候j需要退到不匹配的前一个位置也就是j = pnext[j-1]至于为啥要退到这,简单来说就是pnext[j-1]是重复的个数,下面上代码
def kmp(string,substring):
pnext = back_next(substring)
print(pnext)
m,n,i,j = len(string),len(substring),0,0
while i<m and j<n:
if string[i] == substring[j]:
i+=1
j+=1
elif j!=0:
j = pnext[j-1]
else:
i+=1
return j==n
def back_next(string):
back_next = [0 for i in range(len(string))]
for i in range(len(string)):
tep = 0
if i==0:
continue
for j in range(i):
t = string[:i+1]
if t[:j+1]==t[len(t)-j-1:]:
tep = j+1
back_next[i]=tep
return back_next
作者:王与弓长