MIT线性代数Linear Algebra公开课笔记 第四章 矩阵的LU分解（lecture 4 Factorization into A = LU）

本章是Gilbert Strang的MIT线性代数Linear Algebra公开课中【第四章 矩阵的LU分解（lecture 4 Factorization into A = LU）】的笔记，参考他在 MIT Linear Algebra课程网站上公开分享的 lecture summary (PDF) 和 Lecture video transcript (PDF)等文档，整理笔记如下，笔记中的大部分内容是从 MIT Linear Algebra课程网站上的资料中直接粘贴过来的，本人只是将该课程视频中讲述的内容整理为文字形式，前面的章节可在本人的其他博客中找到（此处戳第一章，第二章，第三章），后面的章节会按照视频顺序不断更新~

文章目录lecture 4 Factorization into A = LU一. Basics（基础知识）1. Inverse of a product2. Transpose of a product二. A = LU（消元的全新认识）三. How expensive is elimination?四. Row exchanges（permutation matrix 置换矩阵） lecture 4 Factorization into A = LU

One goal of today’s lecture is to understand Gaussian elimination in terms of matrices; to find a matrix LLL such that A=LUA=LUA=LU (以总的思路审视高斯消元)。

一. Basics（基础知识） 1. Inverse of a product

 假设矩阵AAA和矩阵BBB可逆（AA−1=I=A−1AAA^{-1}=I=A^{-1}AAA−1=I=A−1A），则它们的乘积ABABAB的逆为B−1A−1B^{-1}A^{-1}B−1A−1，即(AB)−1=B−1A−1(AB)^{-1}=B^{-1}A^{-1}(AB)−1=B−1A−1 .

2. Transpose of a product

  (A−1)T=(AT)−1(A^{-1})^T=(A^T)^{-1}(A−1)T=(AT)−1

二. A = LU（消元的全新认识）

 之前的章节讲述过如何将矩阵AAA 消元为一个上三角矩阵 UUU. This leads to the factorization A=LUA = LUA=LU, which is very helpful in understanding the matrix AAA.

 假设不需要行交换，则矩阵AAA的消元过程可以用 一系列消元矩阵的乘积来表示, 即 A→E21A→E31E21A→⋯→UA \rightarrow E_{21}A \rightarrow E_{31}E_{21}A \rightarrow \cdots \rightarrow UA→E21​A→E31​E21​A→⋯→U.

 Example 1 : (A:2×2)(A: 2×2)(A:2×2)

​  ​ ​ ​​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​  E21E_{21}E21​ ​ ​ ​  AAA ​ ​ ​ ​ ​  UUU
[10−41][2187]=[2103] \left[\begin{array}{rr} {1} & {0} \\ {-4} & {1} \end{array}\right]\left[\begin{array}{ll} {2} & {1} \\ {8} & {7} \end{array}\right]=\left[\begin{array}{ll} {2} & {1} \\ {0} & {3} \end{array}\right] [1−4​01​][28​17​]=[20​13​] 该式可以转化为 A=LUA = LUA=LU形式，而E21E_{21}E21​的逆矩阵即对应的反向操作，通过两端乘以E21−1E_{21}^{-1}E21−1​,变为E21−1E21A=E21−1U=AE_{21}^{-1} E_{21} A=E_{21}^{-1} U=AE21−1​E21​A=E21−1​U=A，则
  ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​   ​ ​ ​ AAA  ​ ​  ​  LLL  ​ ​   UUU
[2187]=[1041][2103] \left[\begin{array}{ll} {2} & {1} \\ {8} & {7} \end{array}\right]=\left[\begin{array}{ll} {1} & {0} \\ {4} & {1} \end{array}\right]\left[\begin{array}{ll} {2} & {1} \\ {0} & {3} \end{array}\right] [28​17​]=[14​01​][20​13​] 矩阵UUU为上三角矩阵（upper triangular），主元在其对角线上，矩阵LLL为下三角矩阵（lower triangular）。

 如果我们将上三角矩阵的主元提取出来，即需要提出一个对角矩阵，即为：

  ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​  ​ ​ AAA  ​ ​ ​  ​ ​ LLL  ​ ​ ​ DDD  ​ ​ ​ U′U'U′
[2187]=[1041][2003][11/201] \left[\begin{array}{ll} {2} & {1} \\ {8} & {7} \end{array}\right]=\left[\begin{array}{ll} {1} & {0} \\ {4} & {1} \end{array}\right]\left[\begin{array}{ll} {2} & {0} \\ {0} & {3} \end{array}\right]\left[\begin{array}{ll} {1} & {1 / 2} \\ {0} & {1} \end{array}\right] [28​17​]=[14​01​][20​03​][10​1/21​]Example 2 : (A:3×3)(A: 3×3)(A:3×3)

 消元的具体过程的矩阵形式，表达如下（消元顺序固定，且假设没有行交换，即无主元为0）：
E21→E31→E32 E_{21} \rightarrow E_{31} \rightarrow E_{32} E21​→E31​→E32​ 即
E32E31E21A=EA=U E_{32} E_{31} E_{21} A=EA=U E32​E31​E21​A=EA=U  则
A=E−1U=E21−1E31−1E32−1U=LU A=E^{-1}U=E{21}^{-1} E{31}^{-1} E_{32}^{-1} U=LU A=E−1U=E21−1E31−1E32−1​U=LU 我们并不关心EEE，只关心右侧"EijE_{ij}Eij​的逆的返顺序乘积"的结果，即LLL。若假设E31E_{31}E31​是单位阵（相当于矩阵AAA的313131位置已经是000了，无需进行消元），而E32E_{32}E32​和E21E_{21}E21​的值如下：
E32=[1000100−51]，E21=[100−210001] E_{32}=\left[\begin{array}{rrr}{1} & {0} & {0} \\ {0} & {1} & {0} \\ {0} & {-5} & {1}\end{array}\right]， E_{21}=\left[\begin{array}{rrr}{1} & {0} & {0} \\ {-2} & {1} & {0} \\ {0} & {0} & {1}\end{array}\right] E32​=⎣⎡​100​01−5​001​⎦⎤​，E21​=⎣⎡​1−20​010​001​⎦⎤​  则
E=E32E21=[1000100−51][100−210001]=[100−21010−51] , left of A，EA=U E=E_{32} E_{21}=\left[\begin{array}{rrr} {1} & {0} & {0} \\ {0} & {1} & {0} \\ {0} & {-5} & {1} \end{array}\right]\left[\begin{array}{rrr} {1} & {0} & {0} \\ {-2} & {1} & {0} \\ {0} & {0} & {1} \end{array}\right]=\left[\begin{array}{rrr} {1} & {0} & {0} \\ {-2} & {1} & {0} \\ {10} & {-5} & {1} \end{array}\right] \text{ , left of A}， EA=U E=E32​E21​=⎣⎡​100​01−5​001​⎦⎤​⎣⎡​1−20​010​001​⎦⎤​=⎣⎡​1−210​01−5​001​⎦⎤​ , left of A，EA=U 乘积的结果中，矩阵的对角线上都是1，而上面都是0，这是因为消元时，我们只有向下操作，即只在下面的行中做了减法，但是却没有向上操作。（结果矩阵中10的由来：因为先从行二中减去两倍的行一，然后从行三种减去五倍的新行二，故行一对行三的影响就是：总共在行三中加上了10倍的行一）。

 下面进行反向计算（reverse order），即计算逆（inverse），则
L=E−1=E21−1E32−1=[100210001][100010051]=[100210051] , left of U，A=LU L=E^{-1}=E_{21}^{-1} E_{32}^{-1}= \left[\begin{array}{lll}{1} & {0} & {0} \\ {2} & {1} & {0} \\ {0} & {0} & {1}\end{array}\right]\left[\begin{array}{lll}{1} & {0} & {0} \\ {0} & {1} & {0} \\ {0} & {5} & {1}\end{array}\right] =\left[\begin{array}{lll}{1} & {0} & {0} \\ {2} & {1} & {0} \\ {0} & {5} & {1}\end{array}\right] \text{ , left of U}， A=LU L=E−1=E21−1​E32−1​=⎣⎡​120​010​001​⎦⎤​⎣⎡​100​015​001​⎦⎤​=⎣⎡​120​015​001​⎦⎤​ , left of U，A=LU 该等式的计算过程：
 可以利用反向操作的意义分别求出消元矩阵E32E_{32}E32​, E21E_{21}E21​ 的逆矩阵（如：E21E_{21}E21​为行二减两倍的行一，则它的反向操作是行二加两倍的行一，即为E21−1E_{21}^{-1}E21−1​）；然后两个逆矩阵相乘，相当于利用左边的矩阵E21−1E_{21}^{-1}E21−1​对右边的矩阵E32−1E_{32}^{-1}E32−1​进行消元（利用消元矩阵的意义，可以直接得出最终结果LLL）；因此，求LLL的过程中，不需要任何运算，只要把所有的消元乘数都写到矩阵中，则直接得到LLL.

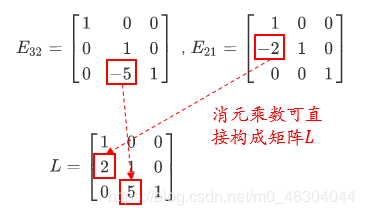
 在消元过程中，只要消元步骤正确，可以在得到LULULU的过程中把AAA抛开，因为AAA的信息都包含在LLL和UUU中了。

三. How expensive is elimination?

 How many operations on an nnn by nnn matrix AAA？共执行了多少次操作

 若 n=100n=100n=100，那么矩阵AAA在实际消元中需要多少次操作？（假设矩阵中没有任何000，因为如果矩阵中有很多地方都是000的话，就不需要那么多次操作了，消元会快很多。）

 一次操作：乘法+减法 为一次操作（multiply plus a subtract）；至于总的操作数，直接看有多少数改变了即可。

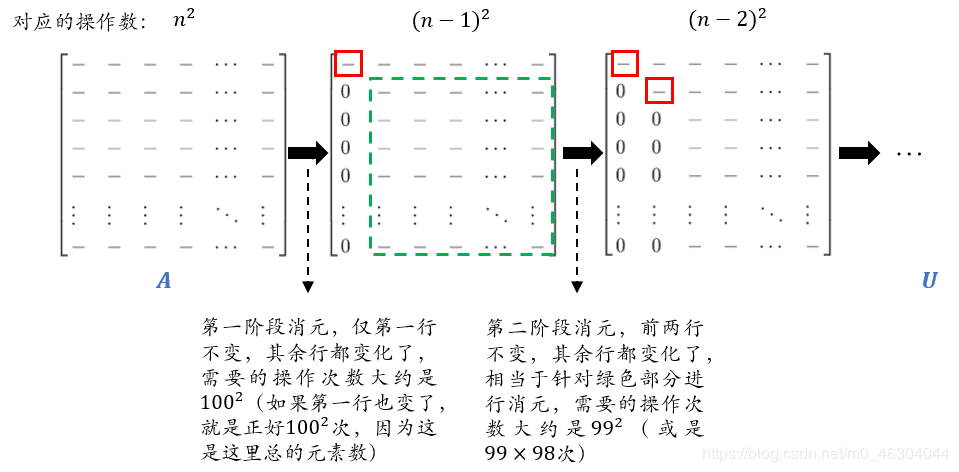
  综上，总的操作次数为
12+22+⋯+(n−1)2+n2=∑i=1ni2≈∫0nx2dx=13n3 1^{2}+2^{2}+\cdots+(n-1)^{2}+n^{2}=\sum_{i=1}^{n} i^{2} \approx \int_{0}^{n} x^{2} d x=\frac{1}{3} n^{3} 12+22+⋯+(n−1)2+n2=i=1∑n​i2≈∫0n​x2dx=31​n3 以上的消元过程仅仅是关于系数矩阵AAA的；在解方程组时，右侧向量bbb也需要消元，如果将右侧向量bbb也放上（bbb只有一列，因此所需操作比较少），消元后，还要进行回代，右侧向量共需要n2n^2n2次操作。

四. Row exchanges（permutation matrix 置换矩阵）

 置换矩阵：用来进行行交换

 Example 3： (3×3)(3×3)(3×3) 共有六种置换矩阵，具体如下：

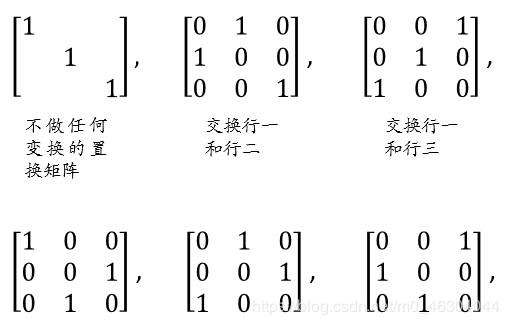
 如果他们两两相乘，乘积结果仍然在这6个当中，因为重复进行的仍然是行变换；如果取其逆，则只是将行换回去即可，因此逆也在这6个结果当中。

  注意：置换矩阵PPP的一个重要性质：P1=PTP^{1}=P^TP1=PT.

  对于(4×4)(4×4)(4×4) 的矩阵，共有24种置换矩阵。

作者：WongRUIRui

mit INTO linear 矩阵