泛化误差上界的证明【内含霍夫丁不等式(Hoeffding's Inequality)的证明】
本篇博客旨在补充李航老师在《统计学习方法》第一章中关于Hoeffding’s Inequality的证明,明白了它 的由来才能对泛化误差上界有更深刻的认识。
温馨提示:最好在电脑端阅读,因为手机屏幕太小,所书写的公式无法施展才华。但是如果可以容忍一丢丢瑕疵的话,也可以在手机上阅读。
泛化能力表示学习方法学习到的模型对未知数据的预测能力。
二、 泛化误差(generalization error) 泛化误差表示用学习到的模型对未知数据进行预测的误差,定义如下:(假设学到的模型为f^\widehat{f}f,L为损失函数)
Rexp(f^)=Ep[L(Y,f^(X)]=∫X×YL(y,f^(x))P(x,y)dxdy \begin{aligned}
R_{exp}(\widehat{f})
& = E_p[L(Y,\widehat{f}(X)] \\
& = \int_{X\times Y} L(y,\widehat{f}(x))P(x,y)dxdy
\end{aligned}Rexp(f)=Ep[L(Y,f(X)]=∫X×YL(y,f(x))P(x,y)dxdy 泛化误差也就是所学模型的误差期望值(即期望风险),反映了学习方法的泛化能力。
对于泛化能力的分析通常是根据泛化误差上界来确定的,因为它代表的是泛化能力的下界,也就是所谓的保底值,如果保底值能够提升,那么模型的整体泛化能力就能够得到提升。
(注意:因为泛化误差定义式中的损失函数所求得的值为负数,所以它必定存在一个上界)
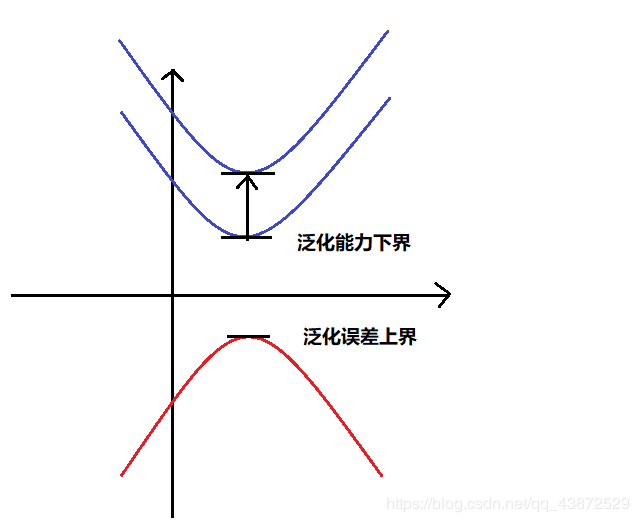
泛化误差上界的定义如下:对于二类分类问题,当假设空间是有限个函数的集合 F={f1,f2,...,fd}\mathcal{F}=\{f_1,f_2,...,f_d\}F={f1,f2,...,fd} 时,对任意一个函数 f∈Ff\in\mathcal{F}f∈F,至少以概率 1−δ (0<δ<1)1-\delta\ (0<\delta<1)1−δ (0<δ<1),使得以下不等式成立:
R(f)≤ R^(f) + ε(d,N,δ)R(f) \leq\ \widehat{R}(f) \ +\ \varepsilon(d,N,\delta)R(f)≤ R(f) + ε(d,N,δ)
其中,
ε(d,N,δ)=12N(logd+log1δ)\varepsilon(d,N,\delta) = \sqrt{\frac{1}{2N}(logd+log\frac{1}{\delta})}ε(d,N,δ)=2N1(logd+logδ1)
不等式中左侧的 R(f)R(f)R(f) 是泛化误差,右侧的即是泛化误差上界,其中的 R^(f)\widehat{R}(f)R(f) 是训练过程中的误差,而 ε(d,N,δ)\varepsilon(d,N,\delta)ε(d,N,δ) 相当于一个纠正量,是 NNN 的单调递减函数,当 NNN 趋近无穷时趋向 0,同时它也是 logdlogdlogd 阶的函数,假设空间包含的函数越多时,ddd 的值越大,即它的值也越大。
值得注意的是,该不等式是根据霍夫丁不等式推导而来,但是霍夫丁不等式同样需要证明是正确的才能进行使用。
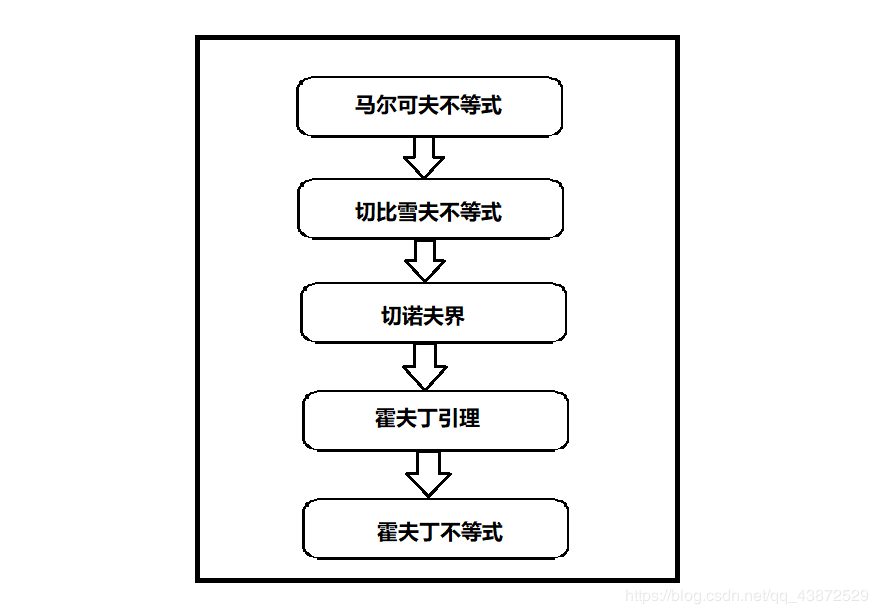
霍夫丁不等式的证明遵循下图中的证明过程,需要先证明马尔可夫不等式、切比雪夫不等式、切诺夫界和霍夫丁引理,才能够对霍夫丁不等式进行证明。
P(Z≥t) ≤ E(Z)tP(Z \ge t)\ \le \ \frac{E(Z)}{t}P(Z≥t) ≤ tE(Z) 证明如下:
P(Z≥t)=E[1{Z≥t}]≤E[Zt1{Z≥t}]≤E(Z)tP(Z \ge t) = E[1_{\{Z \ge t\}} ]\le E[\frac{Z}{t}1_{\{Z \ge t\}} ] \le \frac{E(Z)}{t}P(Z≥t)=E[1{Z≥t}]≤E[tZ1{Z≥t}]≤tE(Z)
注意:1{Z≥t}1_{\{Z \ge t\}}1{Z≥t} 表示的是事件 Z≥tZ\ge tZ≥t 发生的时候为 111,否则为 000。所以当随机情况下,1{Z≥t}≤11_{\{Z \ge t\}} \le 11{Z≥t}≤1。
二、Chebyshev’s Inequality(切比雪夫不等式)
定理:设 ZZZ 是一个属于 RRR 集合的随机变量,且均值为 μ\muμ,方差为 σ2\sigma^2σ2,有:
P(∣Z−μ∣ ≥ σt) ≤ 1t2P(|Z - \mu|\ \ge\ \sigma t)\ \le \ \frac{1}{t^2}P(∣Z−μ∣ ≥ σt) ≤ t21
证明如下:
P(∣Z−μ∣ ≥ σt)=P[ (Z−μ)2≥ σ2t2 ]≤E[ (Z−μ)2 ]σ2t2=σ2σ2t2=1t2 \begin{aligned}
P(|Z - \mu|\ \ge\ \sigma t)
& = \color{red}P[\ (Z-\mu)^2 \ge \ \sigma^2 t^2\ ] \\
& \color{red} \le \frac{E[\ (Z-\mu)^2\ ]}{ \sigma^2 t^2} \color{black} = \frac{ \sigma^2}{\sigma^2 t^2} =\frac{1}{t^2}
\end{aligned}P(∣Z−μ∣ ≥ σt)=P[ (Z−μ)2≥ σ2t2 ]≤σ2t2E[ (Z−μ)2 ]=σ2t2σ2=t21
注意:红色部分使用的是马尔可夫不等式 !!!
三、Chernoff’s bound(切诺夫界) 设 ZZZ 是一个属于 RRR 集合的随机变量,任意的 t>0t>0t>0 ,有:
P(Z≥t) ≤ e−stMZ(s) (s>0)P(Z \ge t)\ \le \ e^{-st} M_Z(s) \ \ \ \ \ \ (s>0)P(Z≥t) ≤ e−stMZ(s) (s>0) 证明如下:对任意的 s>0s>0s>0,
P(Z≥t)=P(sZ≥st)=P(esZ≥est)≤E(esZ)est=MZ(s)est \begin{aligned} P(Z \ge t) & = P(sZ\ge st) \\ & = \color{red}P(e^{sZ}\ge e^{st}) \\ &\color{red} \le \frac{E(e^{sZ})}{e^{st}} \color{black} = \frac{M_Z(s)}{e^{st}} \end{aligned}P(Z≥t)=P(sZ≥st)=P(esZ≥est)≤estE(esZ)=estMZ(s)
注意:红色部分使用的是马尔可夫不等式 !!!
补充内容: MZ(s)M_Z(s)MZ(s) 表示的是矩量母函数(moment-generating function),当满足特定条件时,E(esZ)=MZ(s)E(e^{sZ})=M_Z(s)E(esZ)=MZ(s) 。
四、Hoeffding’s lemma(霍夫丁引理)
定理:设随机变量 Z∈[ a,b ]Z\in [\ a, b\ ]Z∈[ a,b ],对任意的 λ∈R\lambda \in Rλ∈R,有:(这里使用 exp(x)exp(x)exp(x) 代替 exe^xex)
E[ exp( λ(Z−E(Z)) ) ]≤exp(λ2(b−a)28)E[\ exp(\ \lambda(Z-E(Z))\ )\ ]\le exp(\frac{\lambda ^2(b-a)^2}{8})E[ exp( λ(Z−E(Z)) ) ]≤exp(8λ2(b−a)2)
证明:为了使推导过程更加简洁,令E(Z)=0E(Z) = 0E(Z)=0,如果取其他值也并不影响结果,即有:
E[ exp( λ(Z−E(Z)) ) ]=E[ exp(λZ) ](1)E[\ exp(\ \lambda(Z-E(Z))\ )\ ] = E[\ exp(\lambda Z)\ ]\tag{1}E[ exp( λ(Z−E(Z)) ) ]=E[ exp(λZ) ](1)
1. 设 Z=αb+(1−α)aZ = \alpha b +(1-\alpha)aZ=αb+(1−α)a,其中 α=Z−ab−a , 1−α=b−Zb−a\alpha = \frac{Z-a}{b-a}\ ,\ 1-\alpha=\frac{b-Z}{b-a}α=b−aZ−a , 1−α=b−ab−Z,令 g(Z)=exp(λZ)g(Z) = exp(\lambda Z)g(Z)=exp(λZ),因为 g(Z)g(Z)g(Z) 是一个凹函数,所以可以得到:
g(Z)=g[ αb+(1−α)a ]≤αg(b)+(1−α)g(a)=Z−ab−a g(b)+b−Zb−a g(a)=Z−ab−a exp(λb)+b−Zb−a exp(λa)\begin{aligned}
g(Z)
& =g[\ \alpha b +(1-\alpha)a \ ] \\
& \le \alpha g(b)+(1-\alpha)g(a) \\
& = \frac{Z-a}{b-a}\ g(b) + \frac{b-Z}{b-a}\ g(a) \\
& = \frac{Z-a}{b-a}\ exp(\lambda b)+ \frac{b-Z}{b-a}\ exp(\lambda a)
\end{aligned}g(Z)=g[ αb+(1−α)a ]≤αg(b)+(1−α)g(a)=b−aZ−a g(b)+b−ab−Z g(a)=b−aZ−a exp(λb)+b−ab−Z exp(λa)
即得: g(Z)≤Z−ab−a exp(λb)+b−Zb−a exp(λa)(2) g(Z) \le \frac{Z-a}{b-a}\ exp(\lambda b)+ \frac{b-Z}{b-a}\ exp(\lambda a) \tag{2}g(Z)≤b−aZ−a exp(λb)+b−ab−Z exp(λa)(2)
(事实上,在国外的论述中,我们所谓的凹函数是他们的凸函数,它们是根据凹凸性的性质来进行判断,而我们是根据直观的感觉,这一点可以参考百度函数的凹凸性)
2、对不等式(2)两边取期望得:
E[ exp(λZ) ]≤E[ Z−ab−a exp(λb)+b−Zb−a exp(λa) ]=E[ Zb−a (exp(λb)−exp(λa)) ] + E[ bb−a exp(λa)−ab−a exp(λb) ]\begin{aligned}
E[\ exp(\lambda Z)\ ]
& \le E[\ \frac{Z-a}{b-a}\ exp(\lambda b)+ \frac{b-Z}{b-a}\ exp(\lambda a)\ ] \\
& =E[\ \frac{Z}{b-a}\ (exp(\lambda b)-exp(\lambda a))\ ]\ +\\&\ \ \ \ E[\ \frac{b}{b-a}\ exp(\lambda a) -\frac{a}{b-a}\ exp(\lambda b)\ ]
\end{aligned}E[ exp(λZ) ]≤E[ b−aZ−a exp(λb)+b−ab−Z exp(λa) ]=E[ b−aZ (exp(λb)−exp(λa)) ] + E[ b−ab exp(λa)−b−aa exp(λb) ]
即得:
E[ exp(λZ) ]≤E[ Zb−a (exp(λb)−exp(λa)) ] + E[ bb−a exp(λa)−ab−a exp(λb) ](3)\begin{aligned}
E[\ exp(\lambda Z)\ ]
& \le E[\ \frac{Z}{b-a}\ (exp(\lambda b)-exp(\lambda a))\ ]\ +\\&\ \ \ \ E[\ \frac{b}{b-a}\ exp(\lambda a) -\frac{a}{b-a}\ exp(\lambda b)\ ]\tag{3}
\end{aligned}E[ exp(λZ) ]≤E[ b−aZ (exp(λb)−exp(λa)) ] + E[ b−ab exp(λa)−b−aa exp(λb) ](3)
3、又因为 E(Z)=0E(Z)=0E(Z)=0,所以得:
E[ exp(λZ) ]≤E[ bb−a exp(λa)−ab−a exp(λb) ](4)E[\ exp(\lambda Z)\ ]\le E[\ \frac{b}{b-a}\ exp(\lambda a) -\frac{a}{b-a}\ exp(\lambda b)\ ]\tag{4} E[ exp(λZ) ]≤E[ b−ab exp(λa)−b−aa exp(λb) ](4)
4、令 γ=−ab−a\gamma=-\frac{a}{b-a}γ=−b−aa,则有 1−γ=bb−a1-\gamma=\frac{b}{b-a}1−γ=b−ab,即不等式(3)中可以化简为:
E[ exp(λZ) ]≤E[ (1−γ) exp(λa)+γexp(λb) ]=(1−γ) exp(λa)+γexp(λb)\begin{aligned}E[\ exp(\lambda Z)\ ]
& \le E[\ (1-\gamma)\ exp(\lambda a) + \gamma\exp(\lambda b)\ ]\\
&=(1-\gamma)\ exp(\lambda a) + \gamma\exp(\lambda b)
\end{aligned}E[ exp(λZ) ]≤E[ (1−γ) exp(λa)+γexp(λb) ]=(1−γ) exp(λa)+γexp(λb)
即得:
E[ exp(λZ) ]≤(1−γ) exp(λa)+γ exp(λb)(5)E[\ exp(\lambda Z)\ ]\le (1-\gamma)\ exp(\lambda a) + \gamma\ exp(\lambda b) \tag{5}E[ exp(λZ) ]≤(1−γ) exp(λa)+γ exp(λb)(5)
5、令 μ=λ (b−a)\mu = \lambda\ (b-a)μ=λ (b−a),则有 λ a=−μ γ\lambda\ a=-\mu \ \gammaλ a=−μ γ, 即不等式(4)可以化简为:
E[ exp(λZ) ]≤(1−γ) exp(λa)+γ exp(λa) exp(λb)exp(λa)=exp(λa)[ (1−γ) + γ exp(λb)exp(λa) ]=exp(−μ γ) (1−γ + γ exp(μ) )\begin{aligned}E[\ exp(\lambda Z)\ ]
& \le (1-\gamma)\ exp(\lambda a) + \gamma \ exp(\lambda a) \ \frac{exp(\lambda b)}{exp(\lambda a) } \\
& = exp(\lambda a) [\ (1-\gamma)\ +\ \gamma\ \frac{exp(\lambda b)}{exp(\lambda a) }\ ] \\
& = exp(-\mu \ \gamma) \ (1-\gamma\ +\ \gamma\ exp(\mu)\ )
\end{aligned}E[ exp(λZ) ]≤(1−γ) exp(λa)+γ exp(λa) exp(λa)exp(λb)=exp(λa)[ (1−γ) + γ exp(λa)exp(λb) ]=exp(−μ γ) (1−γ + γ exp(μ) )
即得:
E[ exp(λZ) ]≤exp(−μ γ) (1−γ + γ exp(μ) )(6)E[\ exp(\lambda Z)\ ]\le exp(-\mu \ \gamma) \ (1-\gamma\ +\ \gamma\ exp(\mu)\ ) \tag{6}E[ exp(λZ) ]≤exp(−μ γ) (1−γ + γ exp(μ) )(6)
6、令 f(μ)=log[ exp(−μ γ) (1−γ + γ exp(μ) ) ]f(\mu) = log[\ exp(-\mu \ \gamma) \ (1-\gamma\ +\ \gamma\ exp(\mu)\ )\ ]f(μ)=log[ exp(−μ γ) (1−γ + γ exp(μ) ) ],即对应有:E[ exp(λZ) ]≤exp[ f(μ) ]E[\ exp(\lambda Z)\ ]\le exp[\ f(\mu)\ ]E[ exp(λZ) ]≤exp[ f(μ) ],由 f(μ)f(\mu)f(μ) 求导得:
{f′(μ)=−γ+γ exp(μ)1−γ + γ exp(μ)f′′(μ)=γ (1−γ)exp(μ)(1−γ + γ exp(μ) )2\begin{cases}
f^\prime(\mu)=-\gamma +\frac{\gamma\ exp(\mu)}{1-\gamma\ +\ \gamma\ exp(\mu)} \\
\\
f^{\prime \prime}(\mu) = \frac{\gamma\ (1-\gamma)exp(\mu)}{(1-\gamma\ +\ \gamma\ exp(\mu)\ )^2}\\
\end{cases}⎩⎪⎨⎪⎧f′(μ)=−γ+1−γ + γ exp(μ)γ exp(μ)f′′(μ)=(1−γ + γ exp(μ) )2γ (1−γ)exp(μ)
7、根据泰勒定理(Taylor’s Theorem),存在一个 ξ∈(0,μ)\xi \in(0, \mu)ξ∈(0,μ),使得:f(μ)=f(0)+μ f′(0)+μ22 f′′(ξ)f(\mu)=f(0)+ \mu\ f^\prime(0)+\frac{\mu^2}{2}\ f^{\prime \prime}(\xi)f(μ)=f(0)+μ f′(0)+2μ2 f′′(ξ) 成立,由上可知,f(0)=0,f′(0)=0f(0)=0,f^\prime(0)=0f(0)=0,f′(0)=0,即 f(μ)=μ22 f′′(ξ)f(\mu)=\frac{\mu^2}{2}\ f^{\prime \prime}(\xi)f(μ)=2μ2 f′′(ξ)令 t=γ exp(μ)1−γ + γ exp(μ)t=\frac{\gamma\ exp(\mu)}{1-\gamma\ +\ \gamma\ exp(\mu)}t=1−γ + γ exp(μ)γ exp(μ),所以有 f′′(ξ)=t (1−t)≤ 14f^{\prime \prime}(\xi)=t\ (1-t)\le\ \frac{1}{4}f′′(ξ)=t (1−t)≤ 41,即得:f(μ)≤ μ28=λ2 (b−a)28(7)f(\mu)\le \ \frac{\mu^2}{8}=\frac{\lambda^2\ (b-a)^2}{8}\tag{7}f(μ)≤ 8μ2=8λ2 (b−a)2(7)
8、由不等式(6)和(7)以及 f(μ)f(\mu)f(μ) 的定义可得:
E[ exp(λZ) ]≤exp(λ2 (b−a)28)(8)E[\ exp(\lambda Z)\ ] \le exp(\frac{\lambda^2\ (b-a)^2}{8})\tag{8}E[ exp(λZ) ]≤exp(8λ2 (b−a)2)(8)
综上所述可得:E[ exp( λ(Z−E(Z)) ) ]≤exp(λ2 (b−a)28)E[\ exp(\ \lambda(Z-E(Z))\ )\ ]\le exp(\frac{\lambda^2\ (b-a)^2}{8})E[ exp( λ(Z−E(Z)) ) ]≤exp(8λ2 (b−a)2)
到此霍夫丁引理证毕!
P(1N ∑i=1N(Zi−E(Zi))≥t )≤exp(−2Nt2(b−a)2)P( \frac{1}{N}\ \sum_{i=1}^N(Z_i-E(Z_i))\ge t\ )\le exp(-\frac{2Nt^2}{(b-a)^2})P(N1 i=1∑N(Zi−E(Zi))≥t )≤exp(−(b−a)22Nt2) 证明如下:
1、由 P(1N ∑i=1N(Zi−E(Zi))P( \frac{1}{N}\ \sum_{i=1}^N(Z_i-E(Z_i))P(N1 ∑i=1N(Zi−E(Zi)) 可得:P(1N ∑i=1N(Zi−E(Zi))≥t )=P(∑i=1N(Zi−E(Zi)≥Nt)≤E[ es∑i=1N(Zi−E(Zi) ]esNt=∏i=1NE[ es(Zi−E(Zi)) ]esNt\begin{aligned} P( \frac{1}{N}\ \sum_{i=1}^N(Z_i-E(Z_i))\ge t\ ) & = \color{red}P(\sum_{i=1}^N(Z_i-E(Z_i)\ge Nt) \\ & \color{red}\le \frac{E[\ e^{s\sum_{i=1}^N(Z_i-E(Z_i)}\ ]}{e^{sNt}} \\ & = \frac{\prod_{i=1}^N E[\ e^{s(Z_i-E(Z_i))}\ ]}{e^{sNt}} \end{aligned} P(N1 i=1∑N(Zi−E(Zi))≥t )=P(i=1∑N(Zi−E(Zi)≥Nt)≤esNtE[ es∑i=1N(Zi−E(Zi) ]=esNt∏i=1NE[ es(Zi−E(Zi)) ]
注意:红色部分使用的是切诺夫界,其中的 s>0s>0s>0 !!!
即得:
P(1N ∑i=1N(Zi−E(Zi))≤∏i=1NE[ es(Zi−E(Zi)) ]esNt(9)P( \frac{1}{N}\ \sum_{i=1}^N(Z_i-E(Z_i)) \le \frac{\prod_{i=1}^N E[\ e^{s(Z_i-E(Z_i))}\ ]}{e^{sNt}}\tag{9}P(N1 i=1∑N(Zi−E(Zi))≤esNt∏i=1NE[ es(Zi−E(Zi)) ](9)
2、不等式(9)通过霍夫丁引理可化简得:(这里使用 exp(x)exp(x)exp(x) 代替 exe^xex)
P(1N ∑i=1N(Zi−E(Zi))≥t )≤∏i=1NE[ exp[s(Zi−E(Zi))] ]exp(sNt)≤∏i=1Nexp(s2 (b−a)28)exp(sNt)=exp[ Ns2 (b−a)28−sNt ]\begin{aligned} P( \frac{1}{N}\ \sum_{i=1}^N(Z_i-E(Z_i))\ge t\ ) & \le \frac{\prod_{i=1}^N \color{red}E[\ exp[s(Z_i-E(Z_i))]\ ]}{exp(sNt)} \\ & \le \frac{\prod_{i=1}^N \color{red}exp(\frac{s^2\ (b-a)^2}{8})}{exp(sNt)} \\ & = exp[\ \frac{Ns^2\ (b-a)^2}{8}-sNt\ ] \end{aligned} P(N1 i=1∑N(Zi−E(Zi))≥t )≤exp(sNt)∏i=1NE[ exp[s(Zi−E(Zi))] ]≤exp(sNt)∏i=1Nexp(8s2 (b−a)2)=exp[ 8Ns2 (b−a)2−sNt ]即得:
P(1N ∑i=1N(Zi−E(Zi))≥t )≤exp[ Ns2 (b−a)28−sNt ](10)P( \frac{1}{N}\ \sum_{i=1}^N(Z_i-E(Z_i))\ge t\ )\le exp[\ \frac{Ns^2\ (b-a)^2}{8}-sNt\ ]\tag{10}P(N1 i=1∑N(Zi−E(Zi))≥t )≤exp[ 8Ns2 (b−a)2−sNt ](10)
3、令 h(s)=Ns2 (b−a)28−sNth(s)= \frac{Ns^2\ (b-a)^2}{8}-sNth(s)=8Ns2 (b−a)2−sNt,可以看出它是一个关于 sss 的二次函数,且 s>0s>0s>0,因为对称轴:s^=4t(b−a)2>0\widehat{s}=\frac{4t}{(b-a)^2}>0s=(b−a)24t>0,所以函数 h(s)h(s)h(s) 的最小值在对称轴上,即有:
mins>0 exp[ Ns2 (b−a)28−sNt ]= exp(−2Nt2(b−a)2)min_{s>0}\ exp[\ \frac{Ns^2\ (b-a)^2}{8}-sNt\ ]=\ exp(-\frac{2Nt^2}{(b-a)^2})mins>0 exp[ 8Ns2 (b−a)2−sNt ]= exp(−(b−a)22Nt2)
因为要保证不等式(10)恒成立,所以它必须小于函数 h(s)h(s)h(s) 的最小值,即得:
P(1N ∑i=1N(Zi−E(Zi))≥t )≤ exp(−2Nt2(b−a)2)(11)P( \frac{1}{N}\ \sum_{i=1}^N(Z_i-E(Z_i))\ge t\ )\le \ exp(-\frac{2Nt^2}{(b-a)^2}) \tag{11}P(N1 i=1∑N(Zi−E(Zi))≥t )≤ exp(−(b−a)22Nt2)(11)
到此霍夫丁不等式证毕!
紧接着对泛化误差上界进行证明
一、首先我们引入霍夫丁不等式定理
设有 NNN 个独立随机变量 XiX_iXi,都有 Xi∈[ ai,bi ] (i=1,2,...,N )X_i \in [\ a_i, b_i\ ]\ (i=1,2,...,N\ )Xi∈[ ai,bi ] (i=1,2,...,N ),且其中 −∞<ai≤bi<∞,-\infty <a_i\le b_i<\infty,−∞<ai≤bi<∞,X‾\overline{X}X 是 X1,X2,...,XNX_1,X_2,...,X_NX1,X2,...,XN 的实际均值(经验均值),即X‾=1N∑i=1NXi\overline{X}=\frac{1}{N}\sum_{i=1}^NX_iX=N1∑i=1NXi。
则对任意的 t>0t>0t>0,以下不等式成立:
{P( (X‾−E(X‾))≥t )≤exp[ −2N2t2∑i=1N(bi−ai)2 ]P( (E(X‾)−X‾)≥t )≤exp[ −2N2t2∑i=1N(bi−ai)2 ]
\begin{cases}
P( \ ( \overline{X}-E(\overline{X}))\ge t\ )\le exp[\ -\frac{2N^2t^2 }{\sum_{i=1}^N(b_i-a_i)^2}\ ] \\
\\
P( \ ( E(\overline{X})- \overline{X})\ge t\ )\le exp[ \ -\frac{2N^2t^2 }{\sum_{i=1}^N(b_i-a_i)^2}\ ]
\end{cases}⎩⎪⎪⎨⎪⎪⎧P( (X−E(X))≥t )≤exp[ −∑i=1N(bi−ai)22N2t2 ]P( (E(X)−X)≥t )≤exp[ −∑i=1N(bi−ai)22N2t2 ]
以上是霍夫丁不等式的变体,根据原不等式进行了调整(移项),这里用来推导泛化误差上界。
二、然后进入到泛化误差的场景中
1、对任意函数 f∈Ff \in \mathcal{F}f∈F,R^(f)\widehat{R}(f)R(f) 是 NNN 个独立的随机变量 L(Y,f(X))L(Y,f(X))L(Y,f(X)) 的样本均值,R(f)R(f)R(f) 是随机变量 L(Y,f(X))L(Y,f(X))L(Y,f(X)) 的期望值。如果损失函数取值于 [ 0,1 ][\ 0,1\ ][ 0,1 ],即对所有的 i,[ ai,bi ]=[ 0,1 ]i,[\ a_i,b_i\ ]= [\ 0,1\ ]i,[ ai,bi ]=[ 0,1 ],那么由以上不等式可知,对任意的 ε>0\varepsilon>0ε>0,以下不等式成立:
P( R(f)−R^(f)≥ε )≤ exp( −2Nε2 )(12)P(\ R(f)-\widehat{R}(f)\ge \varepsilon\ )\le\ exp(\ -2N\varepsilon^2\ )\tag{12}P( R(f)−R(f)≥ε )≤ exp( −2Nε2 )(12)
{期望风险:R(f)=E[ L(Y,f(X)) ]经验风险:R^(f)=1N∑i=1NL(yi,f(xi))\begin{cases}
期望风险:R(f) = E[\ L(Y,f(X))\ ] \\
\\
经验风险:\widehat{R}(f)=\frac{1}{N}\sum_{i=1}^NL(y_i,f(x_i))
\end{cases}⎩⎪⎨⎪⎧期望风险:R(f)=E[ L(Y,f(X)) ]经验风险:R(f)=N1∑i=1NL(yi,f(xi))
2、由于F={f1,f2,...,fd}\mathcal{F}=\{f_1,f_2,...,f_d\}F={f1,f2,...,fd} 是一个有限集合,故:
P( ∃f∈F:R(f)−R^(f)≥ε )=P( ⋃f∈F{R(f)−R^(f)≥ε })≤ ∑f∈FP(R(f)−R^(f)≥ε )≤d exp(−2Nε2 )\begin{aligned}
P(\ \exists f \in \mathcal{F}: R(f)-\widehat{R}(f)\ge \varepsilon\ )
&= P(\ \bigcup_{f\in \mathcal{F}} \{R(f)-\widehat{R}(f)\ge \varepsilon\ \}) \\
& \le\ \sum_{f\in \mathcal{F}}P(R(f)-\widehat{R}(f)\ge \varepsilon\ )\\
& \le d\ exp( -2N\varepsilon^2\ )
\end{aligned}P( ∃f∈F:R(f)−R(f)≥ε )=P( f∈F⋃{R(f)−R(f)≥ε })≤ f∈F∑P(R(f)−R(f)≥ε )≤d exp(−2Nε2 )
3、等价的,对于任意的 f∈Ff \in \mathcal{F}f∈F,有:
P( R(f)−R^(f)<ε )≥ 1−d exp( −2Nε2 )(13)P(\ R(f)-\widehat{R}(f)< \varepsilon\ )\ge\ 1- d\ exp(\ -2N\varepsilon^2\ )\tag{13}P( R(f)−R(f)<ε )≥ 1−d exp( −2Nε2 )(13)
4、令 δ=d exp( −2Nε2 )\delta = d\ exp(\ -2N\varepsilon^2\ )δ=d exp( −2Nε2 ),即有 ε=12N(logd+log1δ)\varepsilon = \sqrt{\frac{1}{2N}(logd+log\frac{1}{\delta})}ε=2N1(logd+logδ1),则:
P( R(f)−R^(f)<ε )≥ 1−δ(14)P(\ R(f)-\widehat{R}(f)< \varepsilon\ )\ge\ 1- \delta \tag{14}P( R(f)−R(f)<ε )≥ 1−δ(14)
5、即根据不等式(14)可以得知,至少以 1−δ1-\delta1−δ 的概率可以确定: R(f)−R^(f)<ε(15)R(f)-\widehat{R}(f)< \varepsilon \tag{15}R(f)−R(f)<ε(15)
6、但是我们关心的是泛化能力最差的那一个函数,即泛化误差最小的函数,这样获取的泛化误差上界才更具有普遍性,令经验风险最小化函数为: fN=arg minf∈FR^(f)f_N = arg\ min_{f\in \mathcal{F}}\widehat{R}(f)fN=arg minf∈FR(f) ,即得:
R(fN)=E[ L(Y,fN(X)) ](16)R(f_N)=E[\ L(Y,f_N(X))\ ] \tag{16}R(fN)=E[ L(Y,fN(X)) ](16)
综上所述,泛化误差上界为:
R(fN)−R^(fN)<ε( d,N,δ )R(f_N)-\widehat{R}(f_N)< \varepsilon(\ d,N,\delta\ ) R(fN)−R(fN)<ε( d,N,δ )
到此泛化误差上界证毕!
霍夫丁不等式推导的论文链接:03_hoeffding.pdf
码公式不易,且行且珍惜!
希望能够帮助到各位,感谢阅读!
如有错误,还请指正!
作者:不乏希望