多项式回归与模型泛化
有时候,一次项表达式进行回归误差比较大。给定这样的数据集,以y = 0.5 * X^2 + X + 2加入噪声生成,其图像
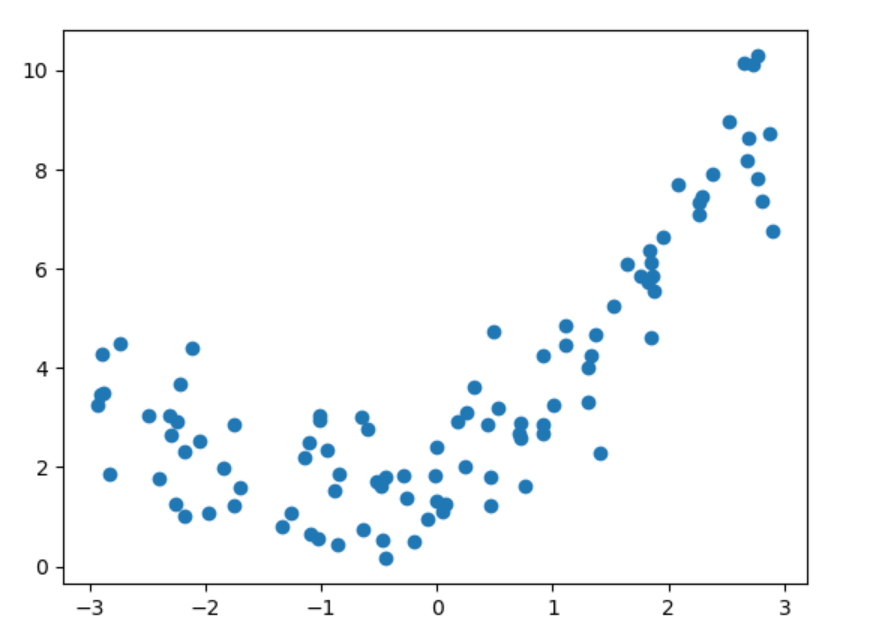
用线性回归获取回归方程,并用预测结果对比实际情况,得到
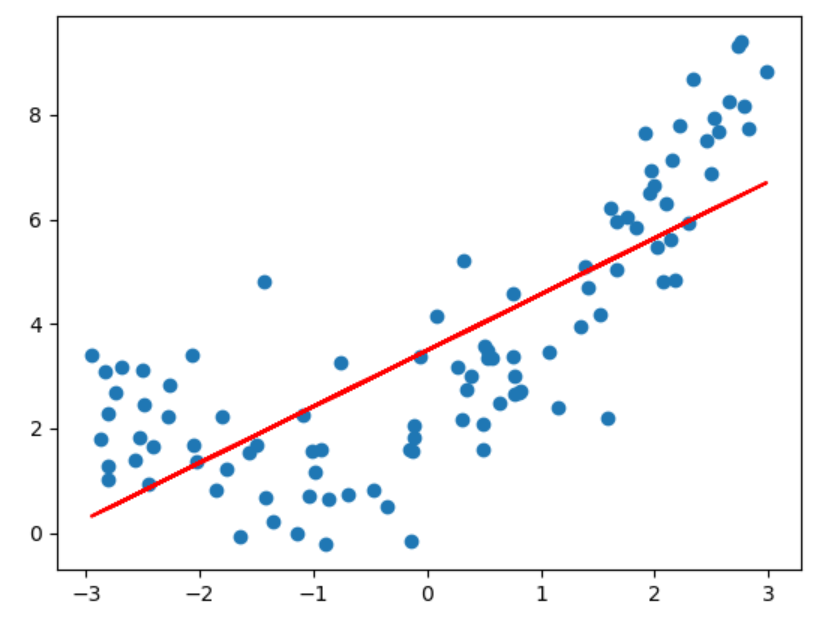
红色直线是通过回归方程得到的所有样本预测值连成的直线,可以看出,一次项式的回归曲线不能很好的完成预测。此时在X样本集中添加X^2作为另一个特征, X_new = np.hstack([X, X**2])为新的特征,并使用线性回归获得回归函数。 加入特征平方项作为新的特征后,得到新的回归曲线明显更好的贴合数据。这种向特征集中加入多次项产生新的特征集并训练模型的方式称为多项式回归。
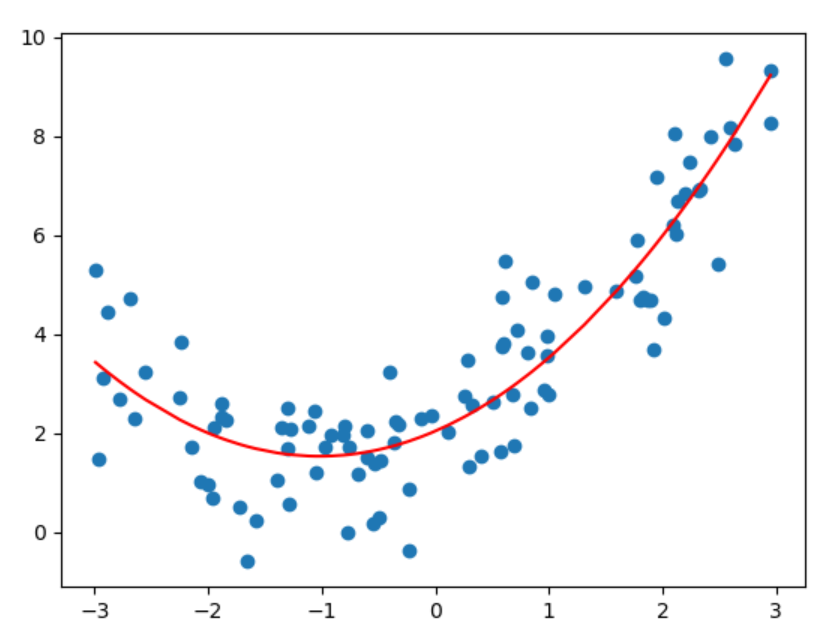
线性回归在sklearn中被封装在linear_model包下的LinearRegression中。但LinearRegression不支持生成含有多项式的特征集,需要使用preprocessing包下的PolynomialFeatures进行生成。
'''使用sklearn中的PolynomialFeatures进行多项式回归'''
poly = PolynomialFeatures(degree=2) # 产生特征数据平方项
poly.fit(X)
# 获得PolynomialFeatures得到的多项式
X_new = poly.transform(X)
# 使用线性回归对X_new进行回归
lin_reg = LinearRegression()
lin_reg.fit(X_new, y)
# 根据线性回归得到预测值
y_predect = lin_reg.predict(X_new)
# 画图
plt.scatter(X, y)
plt.plot(np.sort(x), y_predect[np.argsort(x)], color='r')
plt.show()
创建PolynomialFeatures对象时,传入一个degree参数,这个参数的意思是特征最高次项的项数,这里传入2表示最高产生特征数据平方项。
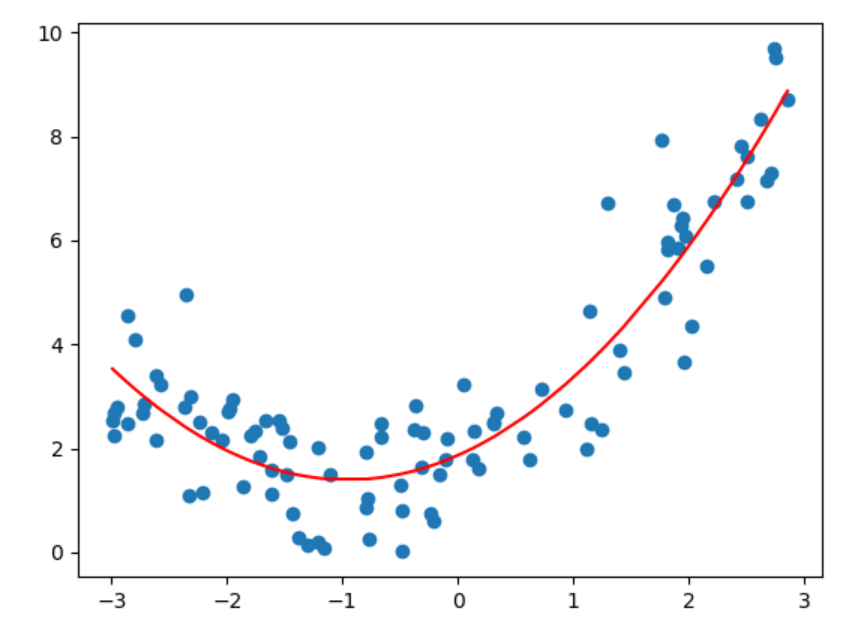
# 查看回归得到的系数
print('X0到X2的系数分别是 %s' % lin_reg.coef_)
print('求得回归曲线截距为 %s' % lin_reg.intercept_)
X0到X2的系数分别是 [[0. 1.04288665 0.53169702]] 求得回归曲线截距为 [1.91589336],可以看到平方项的系数接近0.5,一次项的系数约为1,基本符合创造数据的方式。假设数据有两个特征时,对其进行多项式转换得到的新的数据集什么样?
# 假设数据有两个特征,查看PolynomialFeature生成的多项式矩阵
# 创建特征数据集,一个5 * 2的矩阵
x = np.arange(1, 11)
X = x.reshape(-1, 2)
print(X)
print(x)
poly = PolynomialFeatures(degree=2)
X_new = poly.fit_transform(X)
print('X_new的大小为: ', X_new.shape)
print(X_new)
poly = PolynomialFeatures(degree=3)
X_new = poly.fit_transform(X)
print('X_new的大小为: ', X_new.shape)
print(X_new)
X为5*2矩阵,PolynomialFeatures的degree传入2。打印得到的新特征矩阵
[[ 1 2] [ 3 4] [ 5 6][ 7 8] [ 9 10]]
X_new的大小为[[ 1. 1. 2. 1. 2. 4.][ 1. 3. 4. 9. 12. 16.][ 1. 5. 6. 25. 30. 36.][ 1. 7. 8. 49. 56. 64.][ 1. 9. 10. 81. 90. 100.]]
新矩阵的大小是5 * 6,多了4列。第一列全是1,这是线性回归的默认操作将数据集第一列全部设为1,作为数据的X0。第2、3列是原始数据。第4列是第2列每个数的平方值,第5列是第2列和第3列的乘积,第6列则是第3列的平方值。如果是degree取3
X_new的大小为: (5, 10),[[ 1. 1. 2. 1. 2. 4. 1. 2. 4. 8.][ 1. 3. 4. 9. 12. 16. 27. 36. 48. 64.][ 1. 5. 6. 25. 30. 36. 125. 150. 180. 216.][ 1. 7. 8. 49. 56. 64. 343. 392. 448. 512.][ 1. 9. 10. 81. 90. 100. 729. 810. 900. 1000.]]第1列不用管,记第2列为X1,第3列为X2,第4列可以看出是X1^2,第5列X1 * X2,第6列X2^2,第7列 X1^3,第8列 X1^2 * X2,第9列X2^2 * X1,第10列X2^3。可以看出,PolynomialFeatures会生成新特征矩阵的方式是生成每个特征从二次项到最高次项表达式和所有特征项数相加为最高次项的表达式。这样可以表达各个特征在不同次项上的系数,但可能造成模型的过拟合问题。
使用PipeLine简化过程
之前的步骤中,依次使用PolynomialFeatures对原始数据进行多项式扩充,再使用LinearRegression进行回归。sklearn提供了管道PipeLine可以很方便的将所有步骤简化为一步进行。
'''创建管道进行多项式回归'''
pipe = Pipeline(
[
('poly', PolynomialFeatures(degree=2)), #传入一个PolynomialFeatures
('std', StandardScaler()), #StandardScaler对数据归一化
('lin_reg', LinearRegression()) #传入LinearRegression对象
]
)
print(pipe.fit(X, y))
pipe.fit(X, y)
y_predict = pipe.predict(X)
plt.scatter(X, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()
创造一个Pipeline实例,一次传入PolynomialFeatures等需要使用的对象,之后调用fit即可完成训练。也能得到相应的图像,类似之前的曲线。
交叉验证
为了得到可靠的模型,常用以下方法。之前只是将数据分为训练数据和测试数据两部分,改进一下可以将数据分为三份,分别是训练数据、验证数据和测试数据。训练数据训练出最初的模型,之后使用验证数据进行验证和调参,最后使用测试数据测试。注意,只有测试数据不参与模型训练。 但这样的方式也存在一个问题,数据的划分存在随机性,怎么能够将随机性造成的影响降到最低,应当使用交叉验证的方式。
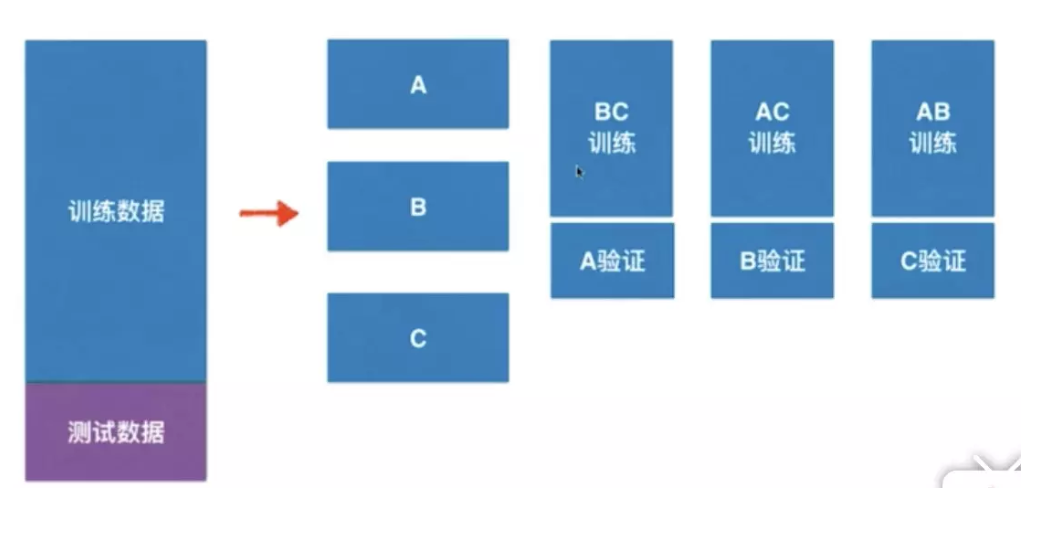
如图给出交叉验证的原理,将训练数据(可以理解为训练数据和验证数据的总称)分为k份,通过不同的组合方式训练出多个模型。通过对每个模型进行测试,计算当前参数下模型准确度的最高的进行作为最优模型,这个衡量标准通常选用准确度均值作为标准进行衡量。交叉验证在sklearn中被封装在model_selection包下的cross_val_score中。
作者:_4444yl