【多视角立体视觉系列】 几何变换的层次——投影变换,仿射变换,度量变换和欧几里德变换
几何变换非常常见,在计算机视觉和图形学上更是如此,而这里指的几何一般是由点,线,面等几何元素组成的1,2维或3维图形。几何变换能够实现不同空间几何元素的对应,在很多领域中有着非常多的应用,立体视觉便是其中一个。本文尝试对四种不同类型的几何变换进行辨析,这些几何变换是一系列计算机视觉处理和相机成像的基础,因此有必要进行掌握。如有谬误,请联系指出,转载请注明出处。
∇\nabla∇ 联系方式:
e-mail: FesianXu@gmail.com
QQ: 973926198
github: https://github.com/FesianXu
研究一个几何问题,一般可以通过两种方式进行,第一种是进行“纯粹”的几何研究,也就是说这种研究应该是和所谓坐标系一点关系都没有的,在不使用任何代数方法的情况下,用几何公理推出其他定理,也就是传统的欧几里德几何;第二种,我们其实也是很熟悉的,就是解析几何,由笛卡尔提出并流行,在这种方法中,我们用代数元素,比如向量去表示几何的点,线,面,用点乘,叉乘去表示元素的一系列操作,从而可以用代数方法进行几何关系的推理。由于现在计算机本质上是对数值进行计算,因此通过解析几何的方法,也就是代数法更容易设计计算机可以解决的算法,因此本文首先要对几何元素进行代数表示。
正如我们在前言所说的,几何元素无非就是点线面,我们在[3]中其实已经初步探讨过为什么要引进齐次坐标这个概念,然而,这里希望重新进行解释,因此我们将从线的代数表示开始说起。
直线我们由中学的知识,知道线在二维空间可以表示为:
ax+by+c=0(1.1)
\begin{aligned}
ax+by+c = 0
\end{aligned}
\tag{1.1}
ax+by+c=0(1.1)
这个线完全由l1=(a,b,c)Tl_1 = (a,b,c)^\mathrm{T}l1=(a,b,c)T 的组合给决定了,因此可以用l1l_1l1这个向量表示这个直线,我们又注意到对于该线来说,式子(1.2)同样成立:
(ka)x+(kb)y+(kc)=0(1.2)
(ka)x+(kb)y+(kc) = 0
\tag{1.2}
(ka)x+(kb)y+(kc)=0(1.2)
而显然,l2=k(a,b,c)Tl_2 = k(a,b,c)^\mathrm{T}l2=k(a,b,c)T和l1l_1l1表示的是同一个直线,于是我们知道,对于这条直线,其表示有无穷多种,此尺度大小也就是kkk只要不为0都是等价的。 特别的,如果k=1ck = \dfrac{1}{c}k=c1那么我们的原先的ccc就变为了1,于是该直线变成了l1=(a,b,1)Tl_1 = (a,b,1)^\mathrm{T}l1=(a,b,1)T,其实只需要两个变量就可以决定一个2D直线了。
需要注意的是,本文用到的每个几何元素都是以列向量的形式表示的,也就是说l1=(a,b,c)Tl_1 = (a,b,c)^\mathrm{T}l1=(a,b,c)T是一个列向量,而其转置(a,b,c)(a,b,c)(a,b,c) 才是行向量。
点怎么表示一个在线上的点呢?既然点在线上,那么自然地,满足式子(1.1),如果把这个式子写成向量乘法的形式,我们有:
(x,y,1)(a,b,c)T=(x,y,1)l=0(1.3)
(x,y,1)(a,b,c)^{\mathrm{T}} = (x,y,1)l = 0
\tag{1.3}
(x,y,1)(a,b,c)T=(x,y,1)l=0(1.3)
说明点p=(x,y,1)Tp = (x,y,1)^\mathrm{T}p=(x,y,1)T在该线上。为什么一个二维的点,会需要在尾巴上多一个1去表示呢?显然,这个是我们之前提到的齐次坐标系[3],但是为什么要这个坐标系,我们虽然之前也提到过,但是本文后面还会继续解释的。
面,一般是存在于三维几何中的概念,其可以表达为:
ax+by+cz+d=0(x,y,z,1)(a,b,c,d)T=0(x,y,z,1)P=0(1.4)
\begin{aligned}
ax+by+cz+d &= 0 \\
(x,y,z,1)(a,b,c,d)^{\mathrm{T}} &= 0 \\
(x,y,z,1)P &= 0
\end{aligned}
\tag{1.4}
ax+by+cz+d(x,y,z,1)(a,b,c,d)T(x,y,z,1)P=0=0=0(1.4)
也就是说,面可以用P=(a,b,c,d)TP = (a,b,c,d)^\mathrm{T}P=(a,b,c,d)T表示,而在面上的点,同样的是在齐次坐标下表示的,为p=(x,y,z,1)Tp = (x,y,z,1)^\mathrm{T}p=(x,y,z,1)T。
我们发现到,无论是点线面,都可以通过一个向量进行表示。
线的相交考虑在二维情况下,我们要如何表示两个线的交点呢?假如给定两个直线l1=(a,b,c)Tl_1 = (a,b,c)^\mathrm{T}l1=(a,b,c)T, l2=(a′,b′,c′)Tl_2 = (a^{\prime}, b^{\prime}, c^{\prime})^\mathrm{T}l2=(a′,b′,c′)T ,定义出向量x=l1×l2x = l_1 \times l_2x=l1×l2,其中的×\times×表示的是叉乘。由向量叉乘的几何意义我们知道,其得到的是正交于两个向量的向量,显然,这两个向量中的任意一个向量正交于lll,也就是有l1⋅(l1×l2)=0,l2⋅(l1×l2)=0l_1 \cdot (l_1 \times l_2) = 0, l_2 \cdot (l_1 \times l_2) = 0l1⋅(l1×l2)=0,l2⋅(l1×l2)=0 也就是l1Tx=l2Tx=0l_1^{\mathrm{T}}x=l_2^{\mathrm{T}}x=0l1Tx=l2Tx=0 ,也就是说向量xxx同时通过了这两条线,显然,他就是交点。
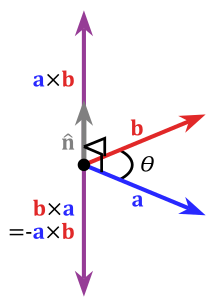
于是我们知道,两个线的交点就是两个线表示的向量的叉乘:
x=l1×l2=[l1]×l2(1.5)
x = l_1 \times l_2 = [l_1]_{\times} l_2
\tag{1.5}
x=l1×l2=[l1]×l2(1.5)
其中的l1=(a,b,c)l_1 = (a,b,c)l1=(a,b,c),而[l1]×[l_1]_{\times}[l1]×是一个矩阵,为:
[l1]×=[0−cbc0−a−ba0](1.6)
[l_1]_{\times} =
\left[
\begin{matrix}
0 & -c & b \\
c & 0 & -a \\
-b & a & 0
\end{matrix}
\right]
\tag{1.6}
[l1]×=⎣⎡0c−b−c0ab−a0⎦⎤(1.6)
圆锥线和二次曲锥面在计算机视觉的几何变换中特别常见,鉴于其篇幅较长,我独立成一篇博文,见[4]。当然,你也可以先不管这个几何元素,直到我们后面提到了IAC, Image of Absolute Conic的时候在回过头复习它。
说在前面——理想点和无限远处的线和面我们在[3]中曾经讨论过理想点(Ideal point)这个概念,简单来说就是平行线交于无穷远处,这个定义可能不够直观,我们借助解析几何,用代数的形式,在齐次坐标的帮助下去定义它。考虑到两个平行线l1:ax+by+c1=0,l2:ax+by+c2=0l_1: ax+by+c_1 = 0, l_2:ax+by+c_2=0l1:ax+by+c1=0,l2:ax+by+c2=0,那么可以表示为l1=(a,b,c1)T,l2=(a,b,c2)Tl_1 = (a,b,c_1)^{\mathrm{T}}, l_2 = (a,b,c_2)^{\mathrm{T}}l1=(a,b,c1)T,l2=(a,b,c2)T,那么由我们上面讨论的,我们知道两个平行线的交点,即便它们是平行线,也可以用叉乘去描述,如l1×l2=(c2−c1)(b,−a,0)Tl_1 \times l_2 = (c_2-c_1)(b,-a,0)^{\mathrm{T}}l1×l2=(c2−c1)(b,−a,0)T,忽略这个尺度因子(c2−c1)(c_2-c_1)(c2−c1),我们发现其交点是(b,−a,0)T(b,-a,0)^{\mathrm{T}}(b,−a,0)T。如果把这个齐次坐标转变为非齐次坐标,我们有(b/0,−a/0)T(b/0, -a/0)^{\mathrm{T}}(b/0,−a/0)T,这个显然是无法计算的,这也意味着平行线的交点都在无穷远处的点上,为了在欧几里德空间中表示这种无穷远处的点,非齐次坐标系是无能为力的,我们只能引入齐次坐标系,也就是在欧几里德空间坐标的基础上,在最后一维再加上一个维度。
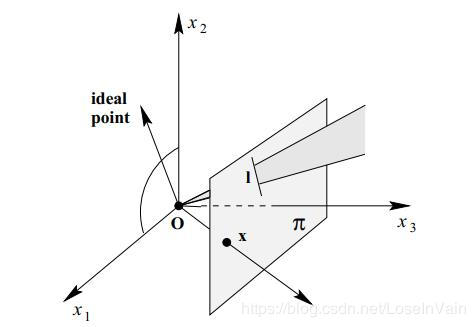
为了考虑平行线的相交的情况,对于二维平面,我们在无限远处假设出了无限远的线(line at infinity),表示为I∞\mathbf{I}_{\infty}I∞ 。对于三维空间来说,我们在无限远处假设出了无限远的平面(plane at infinity),表示为Π∞\Pi_{\infty}Π∞。我们尝试用代数的方式表示这两个元素,我们知道无限远处的点可以表示为p∞=(1,1,0)T\mathbf{p}_{\infty} = (1,1,0)^{\mathrm{T}}p∞=(1,1,0)T(三维情况下要多加一个维度),而无限远处的点应该在无限远处的平面或者线上,那么有
I∞Tp∞=0,二维情况Π∞Tp∞=0,三维情况(2.1)
\mathbf{I}_{\infty}^{\mathrm{T}} \mathbf{p}_{\infty} = 0 , 二维情况 \\
\mathbf{\Pi}_{\infty}^{\mathrm{T}} \mathbf{p}_{\infty} = 0 , 三维情况
\tag{2.1}
I∞Tp∞=0,二维情况Π∞Tp∞=0,三维情况(2.1)
这样就不难得到,这两个元素的一种表达方式为
I∞=(0,0,1)TΠ∞=(0,0,0,1)T(2.2)
\mathbf{I}_{\infty} = (0,0,1)^{\mathrm{T}} \\
\mathbf{\Pi}_{\infty} = (0,0,0,1)^{\mathrm{T}}
\tag{2.2}
I∞=(0,0,1)TΠ∞=(0,0,0,1)T(2.2)
事实上,根据齐次坐标的性质,我们容易知道这两个元素的任意表达方式都是等价的。
在之前的章节中,我们用代数的方式定义了很多几何元素,这些几何元素都是在几何变换中的基本变换单元,在本章节,我们将正式起航,讨论在空间中几何变换。我们首先要考虑的是最为熟悉的欧几里德空间,我们日常生活一般可以建模为欧几里德空间,可以定义出一个原点,然后两个或者三个互为正交的坐标轴,然后客体,也就是我们要研究的物体主体就在这个欧式空间中移动,旋转等,我们会发现,这里如果把客体看成是一个刚体,也就是自身不发生形变的物体,那么客体在欧式空间的旋转,平移等,都是所谓的欧几里德变换(Euclidean transformations)。当然这章暂时只是概念上的辨析,就先不拿出变换公式搞晕各位读者吧。
好的我们继续,注意到,虽然欧几里德空间坐标系一般都有一个原点,有相应的坐标轴,但是这个原点并没有什么特别的地方,坐标轴的方向也没有任何特别的地方,都是我们研究人员为了方便自己设定的,事实上,这个原点和坐标轴我们可以任意的指定,任何一个在有限空间内的,可以用代数表达的原点和坐标轴方向我们都可以指定,只要满足约束条件:
在有限的空间内的,也就是每个原点的分量值都是实数; 坐标轴互相正交欧几里德空间里面的点都是 同质(homogeneous 的,意味着每个在欧式空间的点都是等价的,因此你在平移原点坐标,旋转坐标轴的同时,其实也是在进行着一系列的欧式变换。显然了,欧式变换并不能改变客体的实际长度,毕竟是看作刚体而研究的,同时也改变不了客体的线与线之间的角度,当然,平行线更是不会被改变了,原来相对平行的线,经过欧式变换后仍然还是相对平行的,如Fig 3.1所示。这个当然不是理所当然的,几何变换很多是不保留这些几何元素的,如果大家学过绘画或者摄影,就会发现所谓的透视原理就是典型的一种,不过这个暂且作为后话吧。
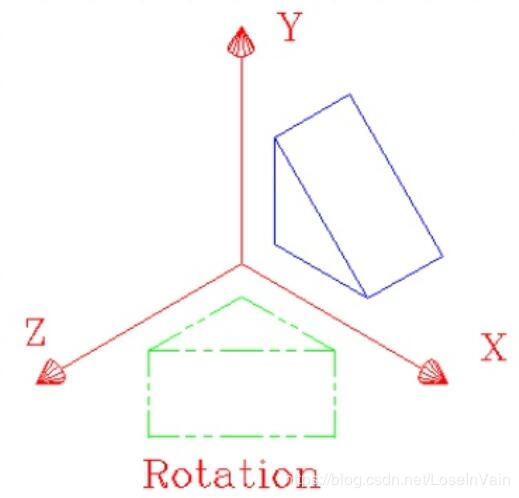
我们对欧几里德变换有了初步的认识,那么欧几里德变换是不是在研究工作中就足够使用了呢?很遗憾,显然不是的,比如计算机图形学中那么多需要对图形进行放大,缩小的操作在欧几里德变换中显然是失效的。因此我们还需要定义一种变换,能使得放大,缩小能够操作起来有理论依据。
这个其实并不困难,我们只需要在保持原点位置,坐标轴的指向方向不变的情况下,将每个坐标轴都“拉伸”或者“缩小”相同的倍数就行了,注意,是每个坐标轴都是相同的倍数。如果结合起欧几里德变换,那么我们就会发现我们可以旋转,平移,放大缩小我们的研究客体了,我们将其称之为相似性变换(similarity transformations)或者度量变换(metric transformations)。注意到,相似性变换包括了欧几里德变换,即是 G{欧几里德变换}⊆G{相似性变换}G\{欧几里德变换\} \subseteq G\{相似性变换\}G{欧几里德变换}⊆G{相似性变换}。
然而,有了放大缩小,我们似乎还是还缺少了一些变换工具,去描述客体在某个特定方向的单独的拉伸或者缩小,而这在某些特殊情况下的成像中是必须的工具(见[5,6]中的仿射相机部分知识点)。于是我们引入了仿射变换(affine transformation),在仿射变换中,每个轴不再是像相似性变换中一样都是放缩同样的倍数了,而是可能放缩不同的尺度。注意到,仿射变换包括了相似性变换和欧几里德变换,即是 G{欧几里德变换}⊆G{相似性变换}⊆G{仿射变换}G\{欧几里德变换\} \subseteq G\{相似性变换\} \subseteq G\{仿射变换\}G{欧几里德变换}⊆G{相似性变换}⊆G{仿射变换}。
这样足够了吗?我们成像出来的物体,在引入了仿射变换之后,也就是如果我们用仿射相机去拍摄一个正方体,会形成如Fig 3.2所示的效果的平面图形(当然,忽视虚线部分)。我们会发现,如果光从这个平面图形,我们完全没法推断出这个客体在三维立体空间的深度信息,客体因为在空间中各个部分距离相机中心的距离或多或少有所不同,正如我们在[7]中的“透视投影的若干性质”中曾经讨论过的,这种因为客体深度不同本应该导致投影缩放(foreshortening)在内的投影变形,而这种变形 表现出来就是远小近大,在客体某些线条就算本身尺度上是一样的,在投影的平面上都可能会产生一定的比例关系。 这种变形有时候正是我们想要的,对于我们人类从平面图形中理解客体在立体工具的深度是不可或缺的存在。因此,如果光用仿射相机,那么形成出来的二维图像就完全失去了推断出客体深度的信息。(如果你的素描老师看到你画的图如Fig 3.2所示,大概会直接挂科吧,RIP)。
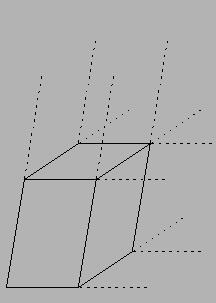
我们该怎么办?相机的初衷是在平面上对客体,对大自然进行复刻,那么自然想要保存更多的原始信息,丢失了深度信息可完全不划算,因此我们还需要引入一个变换形式,我们称之为投影变换(projective transformations),注意到,投影变换包括了仿射变换,相似性变换,欧几里德变换,也就是
G{欧几里德变换}⊆G{相似性变换}⊆G{仿射变换}⊆G{投影变换}
G\{欧几里德变换\} \subseteq G\{相似性变换\} \subseteq G\{仿射变换\} \subseteq G\{投影变换\}
G{欧几里德变换}⊆G{相似性变换}⊆G{仿射变换}⊆G{投影变换}
因此投影变换是一个非常大的种类,其中可以解决我们刚才提到的,在二维平面上体现三维客体的深度信息的成像方法,称之为透视法(perspective),学素描和摄影的读者应该对这个术语很熟悉吧。透视法的原则就是远处的物体看起来小,近处的物体看起来大,所谓的“远小近大”,在透视法中,平行线是会在无穷远处相交的,这个相交点可以称之为消失点(vanish point),联想到我们曾经定义的理想点的概念,我们知道消失点便是理想点。透视法呈现的图像如Fig 3.3所示:
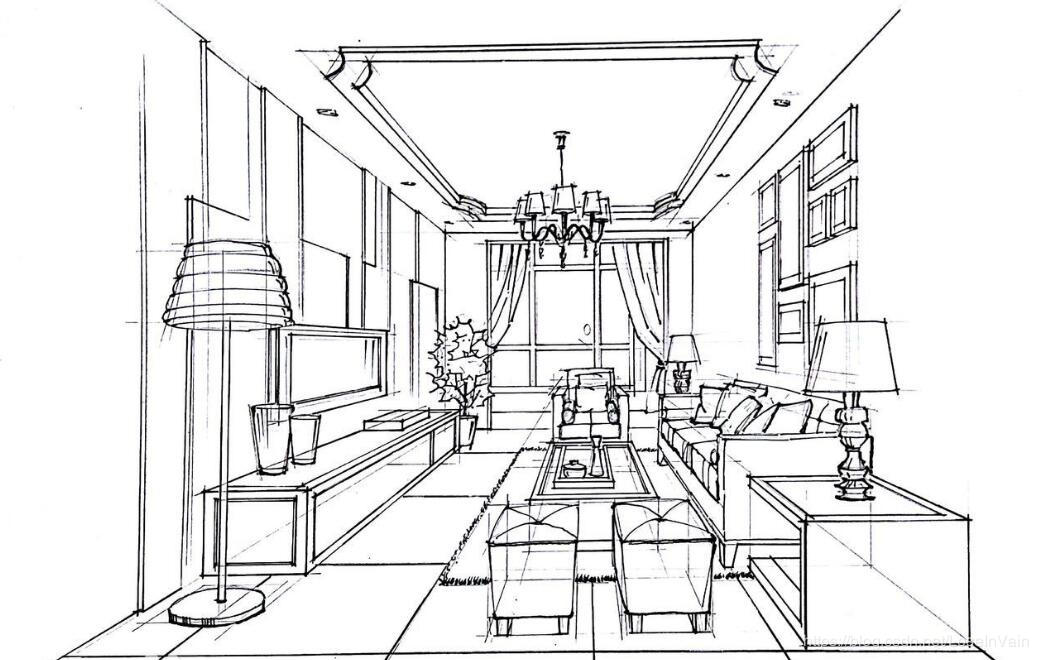
从Fig 3.3中,我们可以通过计算线条比例,从而对场景客体的相对景深进行一定程度上的重建,当然这个重建不是完美的,我们需要很多后续讨论的工具才能更好地进行重建。但是,起码通过投影变换中的透视法,我们能够在二维图像上保存更多的三维客体的信息了。
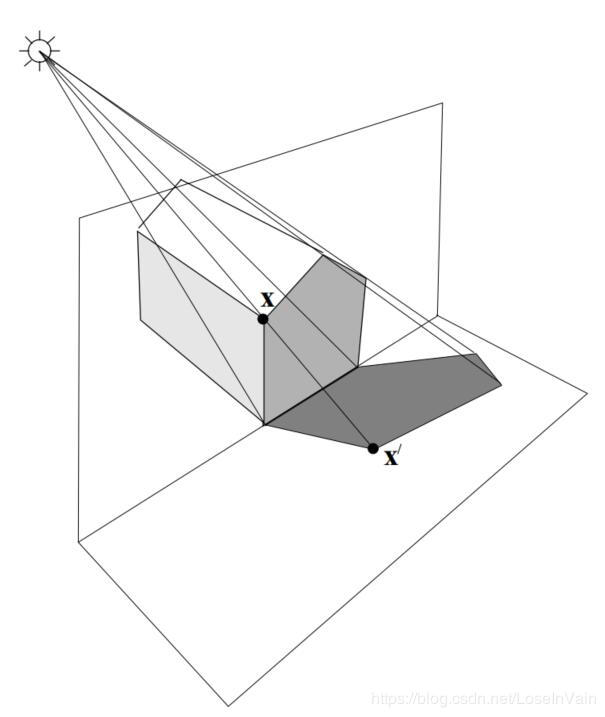
这里我要插个嘴,到底什么叫做投影(projectivity)呢?我们最为直观的印象就是太阳光照着不可透光的房子,形成的倒影,如Fig 3.4所示。这个直观感觉是正确的,确实我们也是这样定义的:
投影性(projectivity)是一种映射hhh,其可以从投影几何空间P2\mathbb{P}^{2}P2(当然也可以是三维的,见下一章节的介绍)映射回这个投影几何空间,使得当且仅当h(x1),h(x2),h(x3)h(\mathbf{x_1}),h(\mathbf{x_2}),h(\mathbf{x_3})h(x1),h(x2),h(x3)三点共线时,x1,x2,x3\mathbf{x_1},\mathbf{x_2},\mathbf{x_3}x1,x2,x3也是共线的。
因此投影线也称之为单应性(homography)[8]或者共线性(colineation),显然共线性这个名称更为形象生动。投影性其实表示的是在投影前后,直线还是直线,该共线的点还是共线的,就那么简单,完事儿。不过多说一句,这种共线性可以用矩阵形式表达,如在二维空间中(用的是齐次坐标系):
h(x)=Hx,H∈R3×3(3.1)
h(\mathbf{x}) = \mathcal{H} \mathbf{x}, \mathcal{H} \in \mathbb{R}^{3 \times 3}
\tag{3.1}
h(x)=Hx,H∈R3×3(3.1)
这就是我们暂时的所有变换了:欧几里德变换,相似性变换,仿射变换和投影变换。当然,在本章节只是从感性的角度去理解这些变换的概念,我们接下来才是正式地步入深入理解这些变换背后的数学含义的章节,让我们继续吧。
投影几何空间和齐次坐标系更配哦~是的你没看错,这一章又会和齐次坐标系扯上关系了,不过我们还是从欧几里德几何空间说起吧。还记得我们的欧几里德空间吗,在这个空间里面的变换不管你怎么变换,无限远处的点永远都在无限远处,而有限的点永远都不可能跑到无限远处对吧,这个是显而易见的。这个性质同样在相似几何空间,仿射几何空间成立,有限远的就是有限远的,无限远的就是无限远的,各自为政,谁也不干扰谁。因此在这些空间去描述变换,实际上并不需要齐次坐标系,只需要非齐次坐标系就足够了,因为我们根本就不需要去描述理想点。
但是,我们还有个投影几何空间,而在这个空间里面,几何变换是很“任性”的,变换前后平行性是得不到保证的,为什么呢?因为正是没办法保证平行性,我们才能提供视觉上的深度信息,这个正是我们想要的。平行性得不到保证,意味着变换前是平行的线,我们知道其交点在理想点处,变化后就可能不再平行了,那么其交点就变成了在有限远处的一个点了,反过来也是成立的。这个在非齐次坐标系下根本没办法解决,毕竟非齐次坐标连理想点和理想线,理想面都没办法描述,又怎么能描述其变换过程呢?因此我们正式引入齐次坐标系,在投影几何空间中,我们必须使用齐次坐标系描述变换过程,为了四个种类变换的公式表达的形式上的统一,我们对于这四种几何空间的变换,一致性地采用齐次坐标系。
那么假设欧几里德空间用R2,R3\mathbb{R}^{2},\mathbb{R}^3R2,R3表示,为了体现投影几何空间的特殊性,我们干脆给他一个表示吧,就表示为P2,P3\mathbb{P}^2, \mathbb{P}^3P2,P3,顺便我们也给仿射空间一个表示A2,A3\mathbb{A}^{2}, \mathbb{A}^3A2,A3 。(别伤心啦,你其实不是顺便的,后面我们还用得上呢,嘿嘿)。
数学形式的四大类型几何变换在用数学形式描述四大类型的几何变换之前,我们要先探讨下,到底什么叫“几何变换”?几何变换不应该只是几个公式咻咻咻地套进去,然后从一堆数字到另一堆数字的过程,几何变换的过程中,我们要留意的是,到底什么几何元素一直没有改变,而什么几何元素可能会改变的。这种变换前后的不变性,对于研究几何变换来说是很重要的,变换的不变性在计算机视觉中也会提供很重要的点子,是一个不可忽视的要点。不管怎么说,我们接下来要留意几何变换的不变性了。注意,接下来的讨论都在三维空间的例子中讨论,涉及到二维空间时将会特别提醒。
投影变换因为投影变换的范围是最广的,其数学形式是最为通用的,于是我们就先从投影变换开始讨论吧。正如式子(3.1)所展示的,我们可以通过线性矩阵变换来描述投影变换,如:
TP=[p11p12p13p14p21p22p23p24p31p22p33p34p41p22p43p44]∈R4×4[X′Y′Z′1]=TP[XYZ1](5.1)
\begin{aligned}
\mathbf{T}_{P} &=
\left[
\begin{matrix}
p_{11} & p_{12} & p_{13} & p_{14} \\
p_{21} & p_{22} & p_{23} & p_{24} \\
p_{31} & p_{22} & p_{33} & p_{34} \\
p_{41} & p_{22} & p_{43} & p_{44}
\end{matrix}
\right] \in \mathbb{R}^{4 \times 4} \\
\left[
\begin{matrix}
X^{\prime} \\
Y^{\prime} \\
Z^{\prime} \\
1
\end{matrix}
\right] &= \mathbf{T}_P
\left[
\begin{matrix}
X \\
Y \\
Z \\
1
\end{matrix}
\right]
\end{aligned}
\tag{5.1}
TP⎣⎢⎢⎡X′Y′Z′1⎦⎥⎥⎤=⎣⎢⎢⎡p11p21p31p41p12p22p22p22p13p23p33p43p14p24p34p44⎦⎥⎥⎤∈R4×4=TP⎣⎢⎢⎡XYZ1⎦⎥⎥⎤(5.1)
注意到TP\mathbf{T}_PTP其实自由度是15,虽然他有16个元素,具体原因见[4]中的关于自由度的说明。在投影变换中,只有共线性,切线性和交叉比(cross-ratio)是不变的。共线性我们之前说过了,切线性指的是,在变换前某个直线是某个曲线的切线,那么变换后这个性质同样保留。投影变换不保留平行性,也不保留无限远处的理想点的位置,因此变换前后,无限可能变成有限,反之亦然。
至于交叉比,我们这样理解,假设客体上有四个点共线,分别是M1,M2,M3,M4M_1, M_2, M_3, M_4M1,M2,M3,M4,那么在选定了参考点之后,其他的共线的点可以被如下式子统一表示:
Mi=M+λiM′(5.2)
M_i = M+\lambda_iM^{\prime}
\tag{5.2}
Mi=M+λiM′(5.2)
那么交叉比表示为:
{M1,M2:M3,M4}=λ1−λ3λ1−λ4:λ2−λ3λ2−λ4(5.3)
\{M_1, M_2:M_3,M_4\} = \dfrac{\lambda_1-\lambda_3}{\lambda_1-\lambda_4}:\dfrac{\lambda_2-\lambda_3}{\lambda_2-\lambda_4}
\tag{5.3}
{M1,M2:M3,M4}=λ1−λ4λ1−λ3:λ2−λ4λ2−λ3(5.3)
这个交叉比的具体比例和参考点的选定无关,并且其在投影变换下保持不变。这个性质为我们通过平面的几何体线条比例去计算客体的相对深度信息提供了依据。
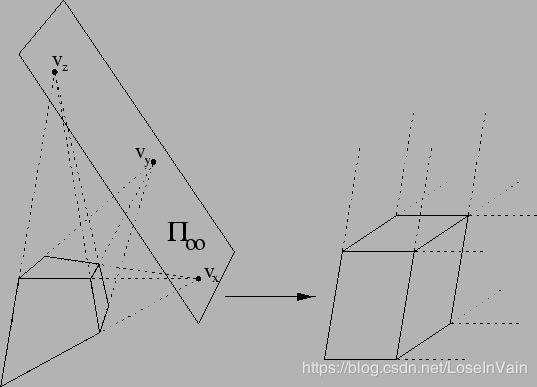
如图Fig 5.1所示,这个是一个特殊的投影变换——透视法后的一个正方体的二维透视图。我们发现平行线相交于理想点Vz,Vy,VxV_z, V_y, V_xVz,Vy,Vx。
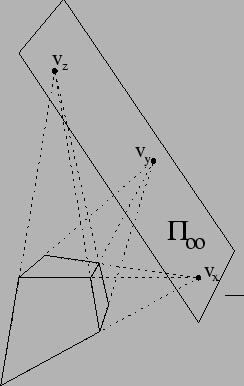
具体的一些消失点的计算,可以参考我以前的博客[9],这里不赘述。
仿射变换仿射变换的数学形式如(5.4)(5.5)所示,可以发现是对投影变换进行了一些元素上的约束后产生的,一般常见的仿射变换子类型包括旋转(rotation),尺度放缩(scale),平移(translation),切变(shear),具体的公式和约束条件见以前的博文[3]。注意到仿射变换前后的不变性继承了投影变换的不变性,也即是共线性,交叉比和切线性。
TA=[a11a12a13a14a21a22a23a24a31a22a33a340001]∈R4×4[X′Y′Z′1]=TA[XYZ1](5.4) \begin{aligned} \mathbf{T}_{A} &= \left[ \begin{matrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{22} & a_{33} & a_{34} \\ 0 & 0 & 0 & 1 \end{matrix} \right] \in \mathbb{R}^{4 \times 4} \\ \left[ \begin{matrix} X^{\prime} \\ Y^{\prime} \\ Z^{\prime} \\ 1 \end{matrix} \right] &= \mathbf{T}_A \left[ \begin{matrix} X \\ Y \\ Z \\ 1 \end{matrix} \right] \end{aligned} \tag{5.4} TA⎣⎢⎢⎡X′Y′Z′1⎦⎥⎥⎤=⎣⎢⎢⎡a11a21a310a12a22a220a13a23a330a14a24a341⎦⎥⎥⎤∈R4×4=TA⎣⎢⎢⎡XYZ1⎦⎥⎥⎤(5.4)
其TA\mathbf{T}_ATA的约束是:
det([a11a12a13a21a22a23a31a22a33])≠0(5.5) \det( \left[ \begin{matrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{22} & a_{33} \end{matrix} \right] ) \neq 0 \tag{5.5} det(⎣⎡a11a21a31a12a22a22a13a23a33⎦⎤)=0(5.5)
容易发现的是,仿射变换的自由度是12,并且容易可以验证仿射变换不会移动无限远处的理想面Π∞\Pi_{\infty}Π∞,可以简单证明下:
在仿射变换后,理想面变成
Π∞′=TA−TΠ∞(5.6)
\Pi_{\infty}^{\prime} = \mathbf{T}_A^{-\mathrm{T}} \Pi_{\infty}
\tag{5.6}
Π∞′=TA−TΠ∞(5.6)
我们从(2.2)知道了对于理想面的表达为Π∞=(0,0,0,1)T\Pi_{\infty} = (0,0,0,1)^{\mathrm{T}}Π∞=(0,0,0,1)T。于是容易验证Π∞′=(0,0,0,1)T\Pi_{\infty}^{\prime} = (0,0,0,1)^{\mathrm{T}}Π∞′=(0,0,0,1)T因此未曾改变理想面。然而,在理想面上的理想点的位置即便没有从无限远处变成有限远处,在仿射变换下也可能在理想面上发生偏移,也就是说仿射变换不保留理想面上点的位置。这一点可以简单证明下,假设理想面上有一个圆锥线[4] xTCx=0\mathbf{x}^{\mathrm{T}} \mathbf{C} \mathbf{x} = 0xTCx=0其中C=I3×3\mathbf{C} = \mathbf{I}_{3 \times 3}C=I3×3单位矩阵,假设仿射变换后有点的位置偏移x′=TAx\mathbf{x}^{\prime} = \mathbf{T}_A\mathbf{x}x′=TAx,那么我们可以知道,变换后的C′=TATCTA=TATTA\mathbf{C}^{\prime} = \mathbf{T}_A^{\mathrm{T}} \mathbf{C} \mathbf{T}_A = \mathbf{T}_A^{\mathrm{T}} \mathbf{T}_AC′=TATCTA=TATTA
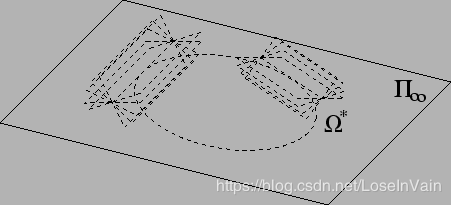
注意到在没有其他约束的情况下,此圆锥线轨迹已经变了。其实这一点也很容易理解,我们对仿射几何空间的坐标轴进行拉伸收缩,每一个轴进行的幅度是不同的,因此在理想面上的圆锥线自然会发生拉伸形变,比如说,可能会从圆形变成椭圆形。(事实上,圆锥曲线在投影变换下等价,这点也容易证明,暂且忽略)。
至于仿射变换的平行性不变性,这点非常容易证明,就留个读者证明吧。
正如我们之前所说的,相似性变换是在欧几里德空间的每个坐标轴都拉伸收缩相同的幅度产生的,那么自然地,理想面上的圆锥曲线形状是不会改变的,至于这个圆锥曲线变得“多大多小”,这种尺度小大的是不影响不变性的。相似性变换的公式如:
TM=[σr11σr12σr13tXσr21σr22σr23tYσr31σr22σr33tZ0001]∈R4×4[X′Y′Z′1]=TM[XYZ1](5.7)
\begin{aligned}\mathbf{T}_{M} &= \left[\begin{matrix}\sigma r_{11} & \sigma r_{12} & \sigma r_{13} & t_X \\\sigma r_{21} & \sigma r_{22} & \sigma r_{23} & t_Y \\\sigma r_{31} & \sigma r_{22} & \sigma r_{33} & t_Z \\0 & 0 & 0 & 1 \end{matrix}\right] \in \mathbb{R}^{4 \times 4} \\\left[\begin{matrix}X^{\prime} \\Y^{\prime} \\Z^{\prime} \\1\end{matrix}\right] &= \mathbf{T}_M\left[\begin{matrix}X \\Y \\Z \\1\end{matrix}\right]\end{aligned}\tag{5.7}
TM⎣⎢⎢⎡X′Y′Z′1⎦⎥⎥⎤=⎣⎢⎢⎡σr11σr21σr310σr12σr22σr220σr13σr23σr330tXtYtZ1⎦⎥⎥⎤∈R4×4=TM⎣⎢⎢⎡XYZ1⎦⎥⎥⎤(5.7)
其中,注意到TM\mathbf{T}_{M}TM存在一些约束:
RM=[r11r12r13r21r22r23r31r32r33]RMTRM=RMRMT=I3×3det(RM)=1(5.8)
\begin{aligned}
\mathbf{R}_{M} &=
\left[
\begin{matrix}
r_{11} & r_{12} & r_{13} \\
r_{21} & r_{22} & r_{23} \\
r_{31} & r_{32} & r_{33}
\end{matrix}
\right] \\
\mathbf{R}_M^{\mathrm{T}} \mathbf{R}_{M} &= \mathbf{R}_{M} \mathbf{R}_M^{\mathrm{T}} = \mathbf{I}_{3 \times 3} \\
\det(\mathbf{R}_M) &= 1
\end{aligned}
\tag{5.8}
RMRMTRMdet(RM)=⎣⎡r11r21r31r12r22r32r13r23r33⎦⎤=RMRMT=I3×3=1(5.8)
也就是说TM\mathbf{T}_MTM的子矩阵RM\mathbf{R}_MRM是一个正交矩阵,并且其行列式值为1(可以视为进行过归一化)。事实上,这里的RM\mathbf{R}_MRM可以视为是旋转矩阵,而tM=(tX,tY,tZ)T\mathbf{t}_M = (t_X, t_Y, t_Z)^{\mathrm{T}}tM=(tX,tY,tZ)T可以视为是将变换前的原点坐标挪到该处,是一个平移偏置向量。而σ\sigmaσ表示的正是对整个客体的放缩尺寸大小。于是我们发现,整个TM\mathbf{T}_MTM的自由度为7,其中3个是朝向相关的自由度,3个是平移相关的,而1个是尺度大小相关的。
考虑到相似性变换前后的不变性,除了继承了仿射变换的不变性之外,还添加了两个重要的新的不变性:**相对距离不变 **和 角度不变。相对距离不变指的是变换前后每个线条的比例是一定的,线条之间的距离的比例也是不变的;角度不变就很好理解了,变换前后,线条之间的夹角不变。
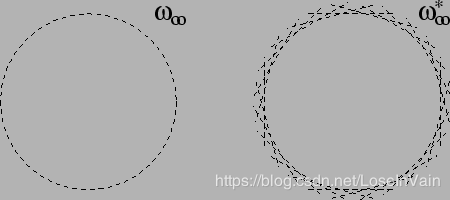
对比仿射变换,相似性变换的理想面的圆锥线有个非常重要的性质,其变换前后形状不变。我们可以尝试对此进行证明。正如Fig 5.2所示,我们假设理想面Π∞\Pi_{\infty}Π∞ 上的二次曲锥面为Ω\OmegaΩ, 但是二次曲锥面是一个立体图形,不容易可视化,我们经常用其对偶二次曲锥面为Ω∗\Omega^{*}Ω∗表示,其表现为一系列的平面。理想面上的二次曲锥面称之为绝对二次曲锥面(Absolute Quadric)。
二次曲锥面是在三维情况下的,在平面上的情况,二次曲锥面就变成了圆锥线ω∞\omega_{\infty}ω∞,其对偶形式为一系列的直线,表示为ω∞∗\omega_{\infty}^*ω∞∗。我们将理想面上的圆锥线称之为绝对圆锥线(Image of Absolute Conic, IAC)。
我们暂且只考虑三维情况下的Ω\OmegaΩ,其最简单的形式就是一个球:
Ω:X2+Y2+Z2=0(5.9) \Omega : X^2+Y^2+Z^2 = 0 \tag{5.9} Ω:X2+Y2+Z2=0(5.9)
其矩阵形式为:
Ω=[1000010000100000](5.10)
\Omega =
\left[
\begin{matrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 \\
\end{matrix}
\right]
\tag{5.10}
Ω=⎣⎢⎢⎡1000010000100000⎦⎥⎥⎤(5.10)
二次曲锥面的方程是xTΩx=0\mathbf{x}^{\mathrm{T}} \mathbf{\Omega} \mathbf{x} = 0xTΩx=0,经过相似性变换后,x′=TMTx\mathbf{x}^{\prime} = \mathbf{T}_M^{\mathrm{T}} \mathbf{x}x′=TMTx。于是变换后,新的二次曲锥面可以表示为:
(TMTx)TΩTMTx=0(5.11)
(\mathbf{T}_M^{\mathrm{T}} \mathbf{x})^{\mathrm{T}} \mathbf{\Omega} \mathbf{T}_M^{\mathrm{T}} \mathbf{x} = 0
\tag{5.11}
(TMTx)TΩTMTx=0(5.11)
Ω′=TMΩTMT(5.12) \mathbf{\Omega}^{\prime} = \mathbf{T}_{M} \mathbf{\Omega} \mathbf{T}_M^{\mathrm{T}} \tag{5.12} Ω′=TMΩTMT(5.12)
为了方便,我们将用分块矩阵的方式计算这个矩阵:
[σRtM03T1][I3×30303T0][σRtM03T1]T(5.13) \left[ \begin{matrix} \sigma \mathbf{R} & \mathbf{t}_M \\ 0_3^{\mathrm{T}} & 1 \end{matrix} \right] \left[ \begin{matrix} \mathbf{I}_{3 \times 3} & 0_3 \\ 0_3^{\mathrm{T}} & 0 \end{matrix} \right] \left[ \begin{matrix} \sigma \mathbf{R} & \mathbf{t}_M \\ 0_3^{\mathrm{T}} & 1 \end{matrix} \right]^{\mathrm{T}} \tag{5.13} [σR03TtM1][I3×303T030][σR03TtM1]T(5.13)
于是有:
Ω′=σ2RI3×3RT=σ2I3×3(5.14)
\mathbf{\Omega}^{\prime} = \sigma^2 \mathbf{R} \mathbf{I}_{3 \times 3} \mathbf{R}^{\mathrm{T}} = \sigma^2 \mathbf{I}_{3 \times 3}\tag{5.14}
Ω′=σ2RI3×3RT=σ2I3×3(5.14)
因为σ\sigmaσ是尺度因子,因此对形状没有影响,我们发现变换前后绝对圆锥线的形状不变。
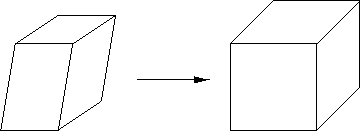
欧几里德变换在相似性变换的基础上,只是把尺度因子σ=1\sigma = 1σ=1设置为了1, 其他不变,因此在继承了相似性变换的所有不变性特性的基础上,又增加了绝对长度不变性。我们有:
TE=[r11r12r13tXr21r22r23tYr31r22r33tZ0001]∈R4×4[X′Y′Z′1]=TE[XYZ1](5.15)
\begin{aligned}\mathbf{T}_{E} &= \left[\begin{matrix}r_{11} & r_{12} & r_{13} & t_X \\r_{21} & r_{22} & r_{23} & t_Y \\r_{31} & r_{22} & r_{33} & t_Z \\0 & 0 & 0 & 1 \end{matrix}\right] \in \mathbb{R}^{4 \times 4} \\\left[\begin{matrix}X^{\prime} \\Y^{\prime} \\Z^{\prime} \\1\end{matrix}\right] &= \mathbf{T}_E\left[\begin{matrix}X \\Y \\Z \\1\end{matrix}\right]\end{aligned}\tag{5.15}
TE⎣⎢⎢⎡X′Y′Z′1⎦⎥⎥⎤=⎣⎢⎢⎡r11r21r310r12r22r220r13r23r330tXtYtZ1⎦⎥⎥⎤∈R4×4=TE⎣⎢⎢⎡XYZ1⎦⎥⎥⎤(5.15)
因此其自由度就只剩下了3个方向自由度,3个平移自由度。
洋洋洒洒地写了一大堆,现在总结下这四大变换的自由度和不变性:
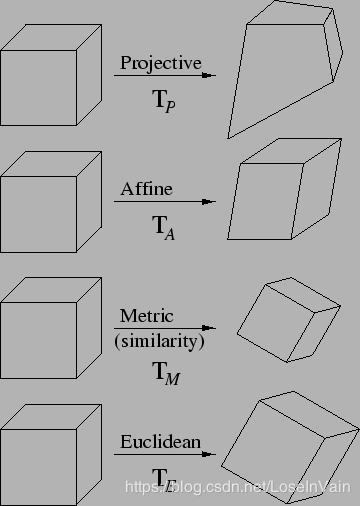
投影变换,自由度15,不变性:交叉比,共线性,切线性。
仿射变换,自由度12,不变性:交叉比,共线性,切线性, 轴方向的相对距离不变,平行不变,理想面不变。
相似性变换,自由度7,不变性:交叉比,共线性,切线性, 轴方向的相对距离不变,平行不变,理想面不变, 相对距离不变,角度不变,绝对圆锥线不变。
欧几里德变换,自由度6,不变性:交叉比,共线性,切线性, 轴方向的相对距离不变,平行不变,理想面不变,相对距离不变,角度不变,绝对圆锥线不变,绝对距离不变。
PS: 本文引出绝对圆锥线的概念,是为了以后的立体视觉中的恢复重建任务和相机参数标定等任务进行铺垫。
Reference[1]. Hartley R, Zisserman A. Multiple View Geometry in Computer Vision[J]. Kybernetes, 2008, 30(9/10):1865 - 1872.
[2]. https://www.cs.unc.edu/~marc/tutorial/node3.html
[3]. https://blog.csdn.net/LoseInVain/article/details/102756630
[4]. https://blog.csdn.net/LoseInVain/article/details/104515839
[5]. https://blog.csdn.net/LoseInVain/article/details/102869987
[6]. https://blog.csdn.net/LoseInVain/article/details/102883243
[7]. https://blog.csdn.net/LoseInVain/article/details/102698703
[8]. https://blog.csdn.net/LoseInVain/article/details/102739778
[9]. https://blog.csdn.net/LoseInVain/article/details/102756630
作者:FesianXu