2019年复旦大学机试题

Leona ·

更新时间:2024-11-13

· 879 次阅读

机试： 一、计算机学院：

1、
在这里插入图片描述
算法笔记上有类似题，且time与time2都是输入。
而本体time是输入，time2是题目给的。
设置time与time2，为计算方便设定让time恒小于time2。
方法：从time（较早的日期）一天一天加，直到time2为止。期间设置一个int型的num来记录相差天数。

#include 
#include 
using namespace std;
int month[13][2] = {{0, 0}, {31, 31}, {28, 29}, {31, 31}, {30, 30}, {31, 31}, {30, 30}, {31, 31}, {31, 31}, {30, 30}, {31, 31}, {30, 30}, {31, 31}};
int isrunnian(int y){
    int flag = 0;
    if((y % 4 == 0 && y % 100 != 0) || y % 400 == 0){
        flag = 1;
    }
    return flag;
}
int main(){
    int time, num = 0;
    int time2 = 20190205;
    scanf("%d", &time);
    if(time > time2){		//time恒小于time2
        int temp = time2;
        time2 = time;
        time = temp;
    }
    int yy = time / 10000, mm = time % 10000 / 100, dd = time % 100;
    int YY = time2 / 10000, MM = time2 % 10000 / 100, DD = time2 % 100;
    while(yy != YY || mm != MM || dd != DD){
        dd++;
        num++;
        if(dd > month[mm][isrunnian(yy)]){
            mm++;
            dd = 1;
        }
        if(mm > 12){
            yy++;
            mm = 1;
        }
    }
    printf("%d", num);
    return 0;
}

2、
在这里插入图片描述
完全是算法笔记的原题，求最大连续子序列和，在这里使用动态规划来解。

#include 
#include 
using namespace std;
const int maxn = 1000010;
int A[maxn], dp[maxn];
int main(){
    int n;
    scanf("%d", &n);
    for(int i = 0; i < n; i++){
        scanf("%d", &A[i]);
    }
    dp[0] = A[0];
    for(int i = 1; i  A[i]){
            dp[i] = dp[i - 1] + A[i];
        }else{
            dp[i] = A[i];
        }
    }
    int ans = dp[0];
    for(int i = 1; i  ans){
            ans = dp[i];
        }
    }
    printf("%d", ans);
    return 0;
}

3、
在这里插入图片描述
emmm，这题要是自己一一实现的话略微困难，而且本题适合用Java的大数来做，用C++会有案例不能通过。
通过百度得知，本题用卡特兰数（Catalan数）可以直接解决。。。

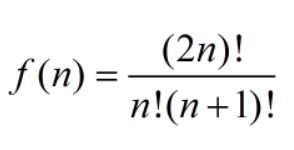
由于Java不会用。。。所以给出C++版本：

#include 
int main(){
    int n;
    scanf("%d", &n);
    long long num, a = 1, b = 1;
    for(int i = 2 * n; i > n; i--){
        a *= i;
    }
    for(int i = n; i > 0; i--){
        b *= i;
    }
    printf("%lld", a / b / (n + 1));
    return 0;
}

对没错，就是这么简单几行代码，不会这个公式就很难，会这个公式轻松解决。不过依旧只能处理n 14则会导致输出错误。

二、工研院：

1、
原创文章 3获赞 2访问量 30 关注私信展开阅读全文
作者：BGLZzz