BZOJ 3124: [Sdoi2013]直径

Georgia ·

更新时间:2024-09-21

· 781 次阅读

题目
简述题意：求直径的必须边。

首先，可通过两次dfs/bfsdfs/bfsdfs/bfs，求出一条直径这里不赘述。

引理：两条直径必有公共点。
证明显然：
假设两条直径无公共点，那么由于树的连通性，我们在把这两条直径连起来一定更长，
与直径的最长性矛盾。

之后我们画图找一下，对于两条直径下的情况。
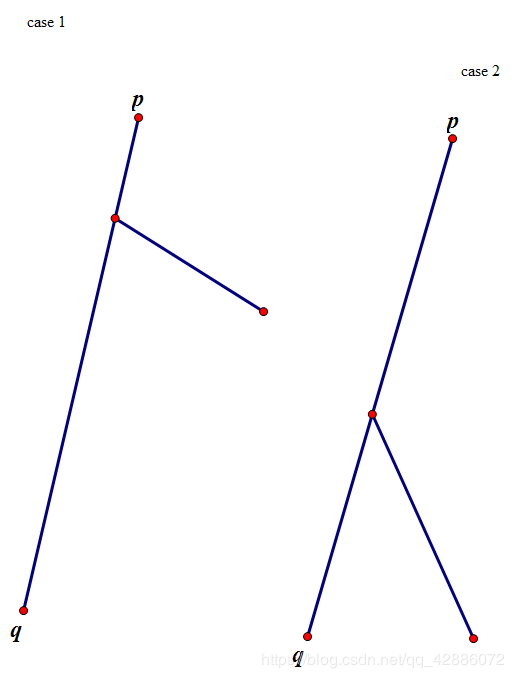
在这里插入图片描述
我们只要求一下满足第一种情况的深度最大值uuu,再求出满足第二种情况的深度最小值vvv,
v−uv-uv−u,即为答案.特殊地，初始化u=0,v=dep[q]u=0,v=dep[q]u=0,v=dep[q].

这是否适用于所有情况呢？答案是显然的。
由于直径必交，而必须边的定义又是属于任意直径，
所以我们只要枚举直径上的点，看是否有合法分叉(能在直径中).
按照上面的求法，我们能保证不违反必须边的定义，同时最大，所以答案正确。

#include
#include
#include
#include
#include
#include
#include
#include
#include
#define fir first
#define sec second
#define lc (x<<1)
#define rc (x<<1|1)
#define g getchar()
#define mk make_pair
#define pi pair
using namespace std;
typedef long long ll;
const int N=2e5+10;
templatevoid qr(o&x) {
	char c=g;int f=1;x=0;
	while(!isdigit(c)){if(c=='-')f=-1;c=g;}
	while(isdigit(c))x=x*10+c-'0',c=g;
	x*=f;
}
templatevoid write(o x) {
	if(x/10)write(x/10);
	putchar(x%10+'0');
}
templatevoid pri(o x) {
	if(x<0)x=-x,putchar('-');
	write(x);puts("");
}
int n,m,dep[N],fa[N];
ll d[N],f[N];
struct edge{int y,next,d;}a[N<d[t]) t=y; f[x]=max(f[x],f[y]+z);
	}
}
int u,v,p,q,sta[N],top;//直径有关信息:p,q为直径端点 
bool in[N];
void find() {
	for(int i=1;i<=n;i++) in[sta[i]]=1;
	while(top) {
		int x=sta[top--];
		for(int k=last[x],y,z;k;k=a[k].next) {
			y=a[k].y; z=a[k].d; if(in[y]) continue;
			if(f[y]+z==f[x]) v=min(v,dep[x]);
			if(f[y]+z==d[x]) u=max(u,dep[x]);
		}
	}
	pri(v-u);
}
int main() {
	qr(n);
	for(int i=1,x,y,z;i<n;i++)	
		qr(x),qr(y),qr(z),ins(x,y,z),ins(y,x,z);
	fa[1]=0; d[1]=0; dep[1]=1; dfs(1,p=1);
	fa[p]=0; d[p]=0; dep[p]=1; dfs(p,q=p);
	pri(d[q]); v=dep[q]; u=1;
	do {
		sta[++top]=q;
		q=fa[q];
	} while(q);
	find(); return 0;
}

作者：zsyzlzy

bzoj

1024 个赞