bzoj 3730. 震波(动态点分治 + vector树状数组)
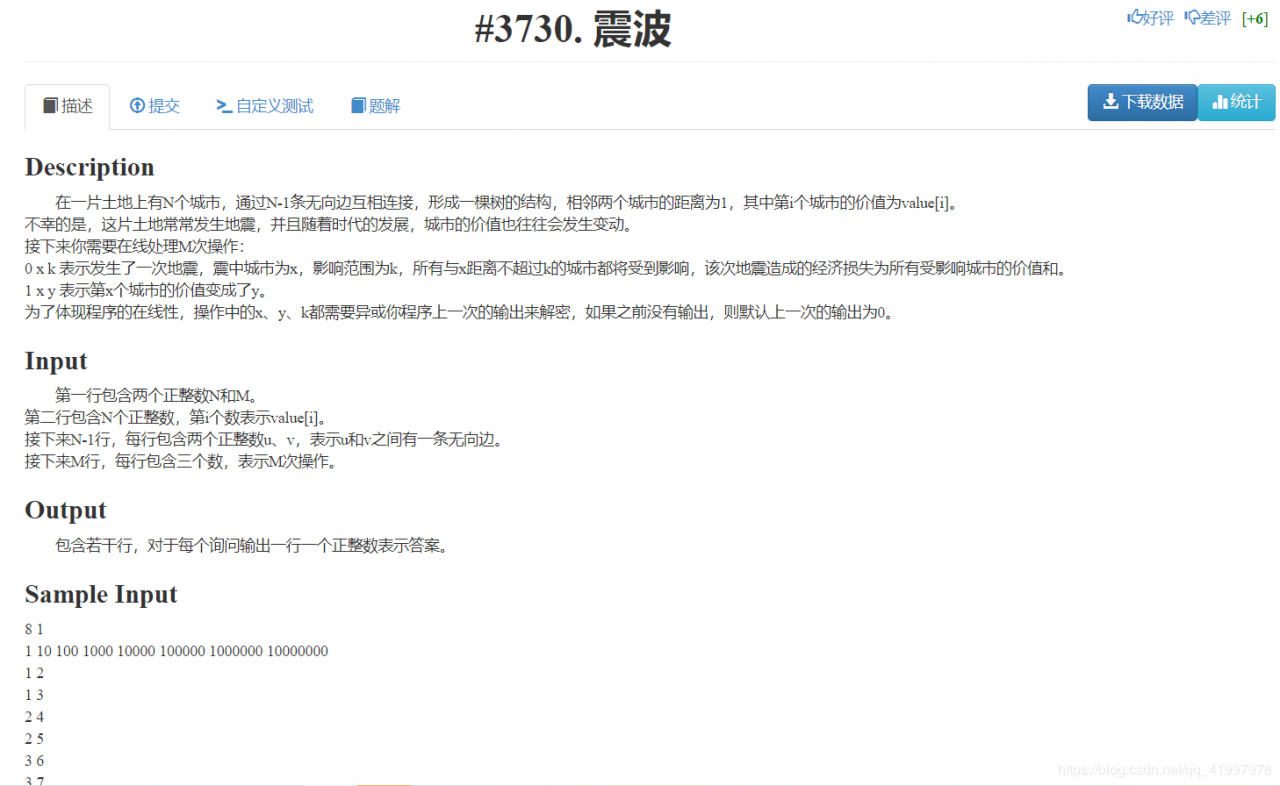
(自己写的动态点分治巨垃圾,常数是别人的两倍)
用动态开点线段树死活过不去,学了一波大佬用 vector 开树状数组立马就卡过去了
考虑点分树的做法,在点分树上每个点以距离为下标建一棵线段树,每次询问查询子树的贡献,再暴力向上跳合并父节点来自其它节点的贡献。
因为子树树形被破坏,在做减法时,子节点子树对父节点的贡献不能用子树维护的信息 + 连向父节点的边的贡献得到,考虑在每个节点再维护一个线段树,按距离建树用来统计子树内的节点到其父节点距离为 p 的点权和,这样便可以暴力爬树统计子树外的节点的贡献。
理论复杂度为 O(nlog2n)O(n \log^2 n)O(nlog2n),但常数巨大,况且还要上动态开点线段树。
采用了别人的用vector开树状数组的做法,首先对空间进行分析:
动态开点线段树:由于树高 logloglog,每次维护要暴力向上爬维护路径上所有节点的信息,显然一个点最多在线段树插入 log\loglog 次,每次插入是单点修改,最多需要新建 log\loglog 个节点,理论空间复杂度上限是 nlog2nn \log^2 nnlog2n
vectorvectorvector 开树状数组:vectorvectorvector 开树状数组最主要要掌握每个节点要开的大小,由于我们维护的是子树信息并且以距离为关键字进行建树维护。每个节点的树状数组大小 = 该节点在点分树上子节点的个数。由于点分树每个节点都是这棵子树的重心,每个子节点的 sizesizesize 的大小大约为父节点 sizesizesize 的 12\frac{1}{2}21,总空间大约为 n+12n+12n+14n+...+1n + \frac{1}{2} n + \frac{1}{2}n + \frac{1}{4}n + ... + 1n+21n+21n+41n+...+1,大概是 nlognn\log nnlogn 级别(不是很准确,大概是这个数字左右)
vectorvectorvector 调用 resize(size)resize(size)resize(size) 函数就可以分配,sizesizesize 大小的空间,如果再传一个参数,将全部赋值为第二个参数的值,最后用树状数组比用线段树快一倍以上。
代码:
#include
using namespace std;
const int maxn = 2e5 + 10;
typedef long long ll;
#define lowbit(i) (i & (-i))
struct Graph {
int head[maxn], to[maxn << 1], cnt, nxt[maxn << 1], w[maxn << 1];
void init() {
memset(head,-1,sizeof head);
cnt = 0;
}
void add(int u,int v,int c) {
to[cnt] = v;
nxt[cnt] = head[u];
w[cnt] = c;
head[u] = cnt++;
to[cnt] = u;
nxt[cnt] = head[v];
w[cnt] = c;
head[v] = cnt++;
}
}G;
vector sum[maxn],fsum[maxn]; //动态开点树状数组
void modify(vector &tree,int p,int v) {
if (p == 0)
tree[0] += v;
else {
for (int i = p; i < tree.size(); i += lowbit(i))
tree[i] += v;
}
}
int ask(vector &tree,int k) {
k = min(k,(int) tree.size() - 1);
int ans = tree[0];
for (int i = k; i; i -= lowbit(i))
ans += tree[i];
return ans;
}
int st[maxn][30],d[maxn],cnt,a[maxn];
int fir[maxn],vis[maxn],f[maxn],root,sz[maxn],siz,p[maxn];
int n,q,RT;
inline int read()
{
int x=0,f=1;char ch;
while(ch'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch f[u]) f[u] = sz[v];
}
if (siz - sz[u] > f[u]) f[u] = siz - sz[u];
if (!root || f[u] sz[u]) siz = all - sz[u];
dfs2(v,u);
p[root] = u; //构建点分树
dfs3(root,u);
}
}
int cal(int u,int v) {
return d[u] fir[y]) swap(x,y);
int p = log2(fir[y] - fir[x] + 1);
return cal(st[fir[x]][p],st[fir[y] - (1 << p) + 1][p]);
}
int getdis(int x,int y) {
return d[x] + d[y] - 2 * d[getlca(x,y)];
}
void prework() {
dfs1(1,0);
for (int i = 1; i <= log2(cnt); i++)
for (int j = 1; j + (1 << i) - 1 <= cnt; j++)
st[j][i] = cal(st[j][i - 1],st[j + (1 << (i - 1))][i - 1]);
root = 0, siz = n; dfs2(1,0);
RT = root; dfs3(root,0); //保留第一次的根节点,并构建点分树
}
void update(int x,int y) {
for (int i = x; i; i = p[i]) {
int dist = getdis(x,i);
modify(sum[i],dist,y);
if (p[i]) modify(fsum[i],getdis(x,p[i]),y);
}
}
int qry(int x,int k) {
int tmp = ask(sum[x],k);
for (int i = x; p[i]; i = p[i]) {
int dist = getdis(x,p[i]);
if (dist <= k) {
tmp += ask(sum[p[i]],k - dist);
tmp -= ask(fsum[i],k - dist);
}
}
return tmp;
}
int main() {
n = read(); q = read();
G.init();
for (int i = 1; i <= n; i++) {
a[i] = read();
}
for (int i = 1; i < n; i++) {
int u,v; u = read(); v = read();
G.add(u,v,1);
}
prework();
for (int i = 1; i <= n; i++)
update(i,a[i]);
int ans = 0;
while (q--) {
int op,x,y; op = read(); x = read(); y = read();
x ^= ans; y ^= ans;
if (op == 1) {
update(x,y - a[x]);
a[x] = y;
} else {
ans = qry(x,y);
printf("%d\n",ans);
}
}
return 0;
}
作者:猝死在学ACM的路上