C语言打印输出杨辉三角
杨辉三角,是二项式系数在三角形中的一种几何排列。
如下图所示:

规律:
1.每行端点与结尾的数为1.
2.每个数等于它上方两数之和。
2.每行数字左右对称,由1开始逐渐变大。
3.第n行的数字有n项。
4.每个数字等于上一行的左右两个数字之和。可用此性质写出整个杨辉三角。即第i+1行的第j个数等于第i行的第j-1个数和第j个数之和,这也是组合数的性质之一。即C(i+1,j)=C(i,j-1)+C(i,j)。
5.第 i 行第 j 个数可表示为:
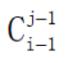
例:
![]()
可以表示为: 7 的阶乘除以(7-3)的阶乘,再除以3的阶乘 即: ( 7! / (7-3)! )/ 3!
以下是笔者所写的代码:(使用了上述规律5)
/* 在屏幕上打印杨辉三角。
by 向前
*/
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
//该函数功能是求传入参数的阶乘
int Factorial(int num){
if (num == 0){
return 1;
} else{
int tmp = num;
for (int i = 1; i < num; ++i){
tmp = tmp*i;
}
return tmp;
}
}
//杨辉三角第 i 行,第 j 个数的值为 C(j-1,i-1)
int Num(int i, int j){
int n = 0;
n = Factorial(i - 1) / Factorial(i - j)/Factorial(j-1);
return n;
}
int main(){
int h = 0;
printf("输入需要打印的行数\n");
scanf("%d", &h); // 可以打印任意行数的杨辉三角
if (h<1){
printf("非法输入!请重新输入\n");
} else{
int s = h - 1;
for (int i = 1; i <= h; ++i){
for (s = h - i; s > 0; --s){ // 该循环是按照规律将空格输出,使之输出为一个三角形
printf(" ");
}
for (int j = 1; j <= i; ++j){
printf(" %d ", Num(i, j));
}
printf("\n\n"); // 每行输出结束后换行
}
}
system("pause");
return 0;
}
编译环境: Visual Studio 2013
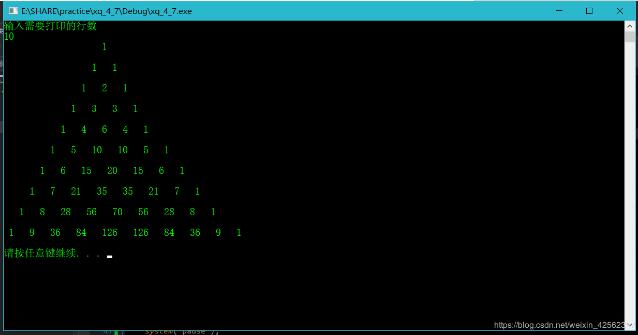
运行效果如下:
相关文章
Nabila
2021-07-22
Lana
2020-12-05
Dolly
2020-01-11
Jacuqeline
2023-07-20
Galatea
2023-07-20
Qamar
2023-07-20
Nancy
2023-07-20
Paula
2023-07-20
Maren
2023-07-20
Lani
2023-07-20
Viveka
2023-07-20
Radinka
2023-07-20
Rayna
2023-07-20
Edda
2023-07-20
Vevina
2023-07-20
Janna
2023-07-20
Levana
2023-07-21
Crystal
2023-07-21