Deep Learning_Task3_过拟合、欠拟合/梯度消失、梯度爆炸/循环神经网络进阶
一、过拟合、欠拟合及其解决方案
·模型选择、过拟合和欠拟合
作者：yonki_e
训练误差(training error)：模型在训练数据集上表现出来的误差
泛化误差(generalization error)：模型在任意一个测试样本上表现出的误差的期望，并常常通过测试数据集上的误差来近似
计算训练误差和泛化误差可以使用损失函数，比如平方损失函数和交叉熵损失函数等
模型选择验证数据集
在严格意义上，测试集只能在所有超参数和模型参数选定后使用一次，不可以使用测试数据选择模型，如调参；而由于无法通过训练误差估计泛化误差，所以也不能只依赖训练数据选择模型
鉴于此，选择预留一部分在训练数据集和测试数据集以外的数据来进行模型选择，这部分数据被称为验证数据集，简称验证集（validation set）
K折交叉验证
目的：为了解决在训练数据不够用时，无法预留出验证数据的情况
K折交叉验证（K-fold-cross-validation）：将原始训练数据集分隔成K个不重合的子数据集，然后作K次模型训练和验证，每一次使用一个子数据集验证模型，并使用其他的K-1个子数据集来训练模型。在K次训练和验证过程中，每次用来验证模型的子数据集都不相同。最后，对K次训练误差和验证误差分别求平均
过拟合和欠拟合模型训练中经常存在的两位典型问题：
1、模型无法得到较低的训练误差，这一现象被成为欠拟合（underfitting）；
2、模型的训练误差远小于其在测试数据集上的误差，这一现象被称为过拟合（overfitting）
导致这两个现象的因素有模型复杂度和训练数据集的大小
模型复杂度
给定训练数据集，模型复杂度和误差之间的关系是：
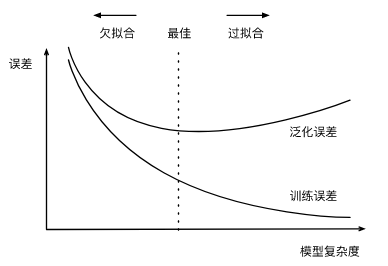训练数据集的大小
一般来说，训练数据集中的样本数过少，特别是比模型参数数量更少时，过拟合更容易发生，此外，泛化误差不会随训练数据集中样本数量的增大而增大，因此，在计算资源允许的范围内，我们通常希望训练数据集大一些，特别是在模型复杂度较高的时候
· 多项式函数拟合实验导入需要的package
import torch
import numpy as np
import sys
import d2lzh as d2l
初始化模型参数
n_train, n_test, true_w, true_b = 100, 100, [1.2, -3.4, 5.6], 5
features = torch.randn((n_train + n_test, 1))
# torch.cat()用来连接列
poly_features = torch.cat((features, torch.pow(features, 2), torch.pow(features, 3)), 1)
labels = (true_w[0] * poly_features[:, 0] + true_w[1] * poly_features[:, 1] + true_w[2] * poly_features[:, 2] + true_b)
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)
定义、训练和测试模型
# Initialize\train\test the model
def semilogy(x_vals, y_vals, x_label, y_label, x2_vals=None, y2_vals=None, legend=None, figsize=(3.5, 2.5)):
# d2l.set_figsize(figsize)
d2l.plt.xlabel(x_label)
d2l.plt.ylabel(y_label)
d2l.plt.semilogy(x_vals, y_vals)
if x2_vals and y2_vals:
d2l.plt.semilogy(x2_vals, y2_vals, linestyle=':')
d2l.plt.legend(legend)
num_epoches, loss = 100, torch.nn.MSELoss()
def fit_and_plot(train_features, test_features, train_labels, test_labels):
# Initialize the net model
net = torch.nn.Linear(train_features.shape[-1], 1)
# set the batch_size
batch_size = min(10, train_labels.shape[0])
# set the dataset
dataset = torch.utils.data.TensorDataset(train_features, train_labels)
# set the method of getting dataset
train_iter = torch.utils.data.DataLoader(dataset, batch_size, shuffle=True)
# set the optimal function_Stochastic gradient descent
optimizer = torch.optim.SGD(net.parameters(), lr=0.01)
train_ls, test_ls = [], []
for _ in range(num_epoches):
# get a batch of dataset
for x, y in train_iter:
# put the data into the net and put the results into the loss function, get the loss
l = loss(net(x), y.view(-1, 1))
# gradient zero to invade the accumulation of gradient
optimizer.zero_grad()
# operate the gradient
l.backward()
# step the optimizer and optimize the parameters
optimizer.step()
train_labels = train_labels.view(-1, 1)
test_labels = test_labels.view(-1, 1)
# save the training loss to the train_ls, and save the test_loss to the test_ls
train_ls.append(loss(net(train_features), train_labels).item())
test_ls.append(loss(net(test_features), test_labels).item())
print('final epoch : train ;loss', train_ls[-1], 'test loss', test_ls[-1])
semilogy(range(1, num_epoches + 1), train_ls, 'epochs', 'loss', range(1, num_epoches + 1), test_ls, ['train', 'test'])
print('weight:', net.weight.data, '\nbias', net.bias.data)
三阶多项式函数拟合（normal）
fit_and_plot(poly_features[:n_train, :], poly_features[n_train:, :], labels[:n_train], labels[n_train:])
Results:
final epoch : train ;loss 9.350672189611942e-05 test loss 0.00010610862955218181
weight: tensor([[ 1.1991, -3.4006, 5.6003]])
bias tensor([5.0013])
overfitting
fit_and_plot(poly_features[0:2, :], poly_features[n_train:, :], labels[0:2], labels[n_train:])
underfitting
fit_and_plot(features[:n_train, :], features[n_train:, :], labels[:n_train], labels[n_train:])
解决过拟合问题的方法
权重衰减——L2范数正则化（regularization）
正则化是通过为损失函数添加惩罚项使学出的模型参数值较小
L2范数正则化
在模型原损失函数的基础上添加L2范数惩罚项，从而得到训练所需要的最小化的函数。L2范数惩罚项是指模型权重参数每个元素的平方和与一个正的常数的乘积
在有了L2范数惩罚项之后，在小批量随机梯度下降中，线性回归中的权重的迭代方程变为：
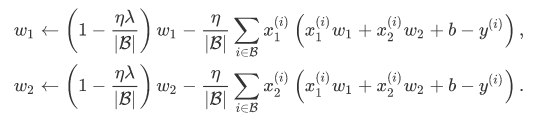
可见，L2范数正则化令权重先自乘小于1的数，再减去不含惩罚项的梯度。因此L2范数正则化，又叫作权重衰减，权重衰减通过惩罚绝对值较大的模型参数为需要学习的模型增加了限制，这可能会对过拟合有效
高维线性回归实验从零开始的实现——L2范数正则化的应用
导入需要的package
import torch
import numpy as np
import torch.nn as nn
import sys
import d2lzh as d2l
初始化模型参数
n_train, n_test, num_inputs = 20, 100, 200
true_w, true_b = torch.ones(num_inputs, 1) * 0.01, 0.05
features = torch.randn((n_train + n_test, num_inputs))
labels = torch.matmul(features, true_w) + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)
train_features, test_features = features[:n_train, :], features[n_train:, :]
train_labels, test_labels = labels[:n_train], labels[n_train:]``
# 定义参数初始化函数，初始化模型参数并且附上梯度
def init_param():
w = torch.randn((num_inputs, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
return [w, b]
定义范数惩罚项
def l2_penalty(w):
return (w**2).sum()/2
定义训练和测试
batch_size, num_epochs, lr = 1, 100, 0.003
net, loss = d2l.linreg, d2l.squared_loss
dataset = torch.utils.data.TensorDataset(train_features, train_labels)
train_iter = torch.utils.data.DataLoader(dataset, batch_size, shuffle=True)
def fit_and_plot(lambd):
w, b = init_params()
train_ls, test_ls = [], []
for _ in range(num_epochs):
for X, y in train_iter:
# 添加了L2范数惩罚项
l = loss(net(X, w, b), y) + lambd * l2_penalty(w)
l = l.sum()
if w.grad is not None:
w.grad.data.zero_()
b.grad.data.zero_()
l.backward()
d2l.sgd([w, b], lr, batch_size)
train_ls.append(loss(net(train_features, w, b), train_labels).mean().item())
test_ls.append(loss(net(test_features, w, b), test_labels).mean().item())
d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
range(1, num_epochs + 1), test_ls, ['train', 'test'])
print('L2 norm of w:', w.norm().item())
观察过拟合
fit_and_plot(lambd = 0)
使用权重衰减
fit_and_plot(lambd = 3)
丢弃法
多层感知机中神经网络图描述了一个单隐藏层的多层感知机。其中输入个数为4，隐藏单元个数为5， 且隐藏单元的计算表达式为：
当对该隐藏层使用丢弃法时，该层的隐藏单元将有一定的概率被丢弃掉，假设丢弃概率为p，那么就有p的概率隐藏单元h被丢弃掉，还有1-p的概率h会除以1-p进行拉伸。丢弃概率是丢弃法的超参数
丢弃法不改变其输入的期望值
那么其输入的期望值为：
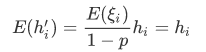
对于多层感知机的神经网络中的隐藏层使用丢弃法，一种可能如图所示
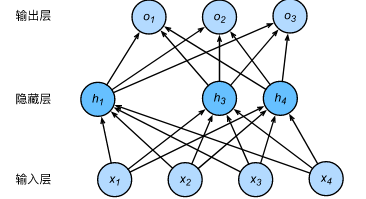即h2和h5被清零，这时输出值的计算不再依赖于h2和h5，在反向传播时，与这两个隐藏单元相关的权重的梯度均为0。由于在训练中隐藏层神经元的丢弃是随机的，所以输出层的计算无法过度依赖于隐藏单元中的个任意一个，从而在训练模型时起到正则化的作用，并可以用来应对过拟合
丢弃法从零开始的实现
导入需要的package
import torch
import numpy as np
import torch.nn as nn
import sys
import d2lzh as d2l
定义丢弃函数
def dropout(x, drop_prob):
x = x.float()
assert 0 <= drop_prob <= 1
keep_pro = 1-drop_prob
if keep_prob == 0:
return torch.zeros_like(x)
mask = (torch.rand(x.shape) < keep_prob).float()
return mask * x / keep_prob
参数初始化
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256
W1 = torch.tensor(np.random.normal(0, 0.01, size=(num_inputs, num_hiddens1)), dtype=torch.float, requires_grad=True)
b1 = torch.zeros(num_hiddens1, requires_grad=True)
W2 = torch.tensor(np.random.normal(0, 0.01, size=(num_hiddens1, num_hiddens2)), dtype=torch.float, requires_grad=True)
b2 = torch.zeros(num_hiddens2, requires_grad=True)
W3 = torch.tensor(np.random.normal(0, 0.01, size=(num_hiddens2, num_outputs)), dtype=torch.float, requires_grad=True)
b3 = torch.zeros(num_outputs, requires_grad=True)
params = [W1, b1, W2, b2, W3, b3]
训练测试
drop_prob1, drop_prob2 = 0.2, 0.5
def net(X, is_training=True):
X = X.view(-1, num_inputs)
H1 = (torch.matmul(X, W1) + b1).relu()
if is_training: # 只在训练模型时使用丢弃法
H1 = dropout(H1, drop_prob1) # 在第一层全连接后添加丢弃层
H2 = (torch.matmul(H1, W2) + b2).relu()
if is_training:
H2 = dropout(H2, drop_prob2) # 在第二层全连接后添加丢弃层
return torch.matmul(H2, W3) + b3
def evaluate_accuracy(data_iter, net):
acc_sum, n = 0.0, 0
for X, y in data_iter:
if isinstance(net, torch.nn.Module):
net.eval() # 评估模式, 这会关闭dropout
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
net.train() # 改回训练模式
else: # 自定义的模型
if('is_training' in net.__code__.co_varnames): # 如果有is_training这个参数
# 将is_training设置成False
acc_sum += (net(X, is_training=False).argmax(dim=1) == y).float().sum().item()
else:
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
n += y.shape[0]
return acc_sum / n
num_epochs, lr, batch_size = 5, 100.0, 256 # 这里的学习率设置的很大，原因与之前相同。
loss = torch.nn.CrossEntropyLoss()
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, root='/home/kesci/input/FashionMNIST2065')
d2l.train_ch3(
net,
train_iter,
test_iter,
loss,
num_epochs,
batch_size,
params,
lr)
二、梯度消失、梯度爆炸以及Kaggle房价预测
·梯度消失和梯度爆炸
深度模型有关数值稳定性的典型问题是消失（vanishing）和爆炸（explosion）
当神经网络的层数较多时，模型的数值稳定性容易变差
原因：如果将每个隐藏单元的参数都初始化为相等的值，那么在正向传播时每个隐藏单元将根据相同的输入计算出相同的值，并传递至输出层。在反向传播时，每个隐藏单元的参数梯度值相等。因此，这些参数在使用基于梯度的优化算法迭代后的值仍然相等。之后的迭代也是这样，所以，在这种情况下，无论隐藏单元有多少，隐藏层本质上只有一个1个隐藏单元在发挥作用。因此，我们通常将神经网络的模型参数，特别是权重参数进行随机初始化
PyTouch的默认初始化
touch.nn.init.normal_()
Xavier随机初始化
假设某全连接层的输入个数为a，输出个数为b，Xavier随机初始化使该层中的权重参数的每个元素都随机采样于均匀分布
他的设计主要考虑到，模型参数初始化后，每层输出的方差不该受该层输入个数的影响，且每层梯度的方差也不该受该层输出个数的影响
协变量偏移
这里我们假设，虽然输入的分布可能会随时间而改变，但是标记函数，即条件分布P(y/x)不会改变
统计学家称协变量变化是因为问题的根源在于特征分布的变化（协变量的变化）。数学上，我们可以说P(x)改变了，但是P(y/x)保持不变。尽管它的有用性并不局限于此，当我们认为x导致y时，协变量移位通常是正确的假设
标签(label)偏移
当我们认为导致偏移的时标签P(y)上的边缘分布的的变化，但类条件分布是不变的P(x/y)时，就会出现相反的问题。当我们认为y导致x时，标签偏移是一个合理的假设，有时标签偏移和协变量移位假设可以同时成立
概念偏移——标签本身的定义发生变化
·Kaggle房价预测实战导入需要的package
import numpy as np
import torch
import torch.nn as nn
import pandas as pd
import sys
import d2lzh as d2l
预处理数据
对连续数值的特征进行标准正态分布
numeric_features = all_features.dtypes[all_features.dtypes != 'object'].index
all_features[numeric_features] = all_features[numeric_features].apply(
lambda x: (x - x.mean()) / (x.std()))
# 标准化后，每个数值特征的均值变为0，所以可以直接用0来替换缺失值
all_features[numeric_features] = all_features[numeric_features].fillna(0)
将离散数值转换成指示特征
# dummy_na=True将缺失值也当作合法的特征值并为其创建指示特征
all_features = pd.get_dummies(all_features, dummy_na=True)
all_features.shape
通过values属性的到numpy格式的数据，并转换成Tensor方便后面的训练
n_train = train_data.shape[0]
train_features = torch.tensor(all_features[:n_train].values, dtype=torch.float)
test_features = torch.tensor(all_features[n_train:].values, dtype=torch.float)
train_labels = torch.tensor(train_data.SalePrice.values, dtype=torch.float).view(-1, 1)
训练模型
loss = torch.nn.MSELoss()
def get_net(feature_num):
net = nn.Linear(feature_num, 1)
for param in net.parameters():
nn.init.normal_(param, mean=0, std=0.01)
return net
对均方根误差的实现
def log_rmse(net, features, labels):
with torch.no_grad():
# 将小于1的值设成1，使得取对数时数值更稳定
clipped_preds = torch.max(net(features), torch.tensor(1.0))
rmse = torch.sqrt(2 * loss(clipped_preds.log(), labels.log()).mean())
return rmse.item()
Adam优化算法
def train(net, train_features, train_labels, test_features, test_labels,
num_epochs, learning_rate, weight_decay, batch_size):
train_ls, test_ls = [], []
dataset = torch.utils.data.TensorDataset(train_features, train_labels)
train_iter = torch.utils.data.DataLoader(dataset, batch_size, shuffle=True)
# 这里使用了Adam优化算法
optimizer = torch.optim.Adam(params=net.parameters(), lr=learning_rate, weight_decay=weight_decay)
net = net.float()
for epoch in range(num_epochs):
for X, y in train_iter:
l = loss(net(X.float()), y.float())
optimizer.zero_grad()
l.backward()
optimizer.step()
train_ls.append(log_rmse(net, train_features, train_labels))
if test_labels is not None:
test_ls.append(log_rmse(net, test_features, test_labels))
return train_ls, test_ls
K折交叉验证
def get_k_fold_data(k, i, X, y):
# 返回第i折交叉验证时所需要的训练和验证数据
assert k > 1
fold_size = X.shape[0] // k
X_train, y_train = None, None
for j in range(k):
idx = slice(j * fold_size, (j + 1) * fold_size)
X_part, y_part = X[idx, :], y[idx]
if j == i:
X_valid, y_valid = X_part, y_part
elif X_train is None:
X_train, y_train = X_part, y_part
else:
X_train = torch.cat((X_train, X_part), dim=0)
y_train = torch.cat((y_train, y_part), dim=0)
return X_train, y_train, X_valid, y_valid
def k_fold(k, X_train, y_train, num_epochs,
learning_rate, weight_decay, batch_size):
train_l_sum, valid_l_sum = 0, 0
for i in range(k):
data = get_k_fold_data(k, i, X_train, y_train)
net = get_net(X_train.shape[1])
train_ls, valid_ls = train(net, *data, num_epochs, learning_rate,
weight_decay, batch_size)
train_l_sum += train_ls[-1]
valid_l_sum += valid_ls[-1]
if i == 0:
d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'rmse',
range(1, num_epochs + 1), valid_ls,
['train', 'valid'])
print('fold %d, train rmse %f, valid rmse %f' % (i, train_ls[-1], valid_ls[-1]))
return train_l_sum / k, valid_l_sum / k
模型选择
我们使用一组未经调优的超参数并计算交叉验证误差。可以改动这些超参数来尽可能减小平均测试误差
k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
train_l, valid_l = k_fold(k, train_features, train_labels, num_epochs, lr, weight_decay, batch_size)
print('%d-fold validation: avg train rmse %f, avg valid rmse %f' % (k, train_l, valid_l))
预测并在Kaggle中提交结果
def train_and_pred(train_features, test_features, train_labels, test_data,
num_epochs, lr, weight_decay, batch_size):
net = get_net(train_features.shape[1])
train_ls, _ = train(net, train_features, train_labels, None, None,
num_epochs, lr, weight_decay, batch_size)
d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'rmse')
print('train rmse %f' % train_ls[-1])
preds = net(test_features).detach().numpy()
test_data['SalePrice'] = pd.Series(preds.reshape(1, -1)[0])
submission = pd.concat([test_data['Id'], test_data['SalePrice']], axis=1)
submission.to_csv('./submission.csv', index=False)
# sample_submission_data = pd.read_csv("../input/house-prices-advanced-regression-techniques/sample_submission.csv")
train_and_pred(train_features, test_features, train_labels, test_data, num_epochs, lr, weight_decay, batch_size)
三、ModernRNN
·GRU
RNN存在的问题：梯度容易出现衰减或爆炸（BPTT）
门控循环神经网络：捕捉时间序列中时间步距离较大的依赖关系
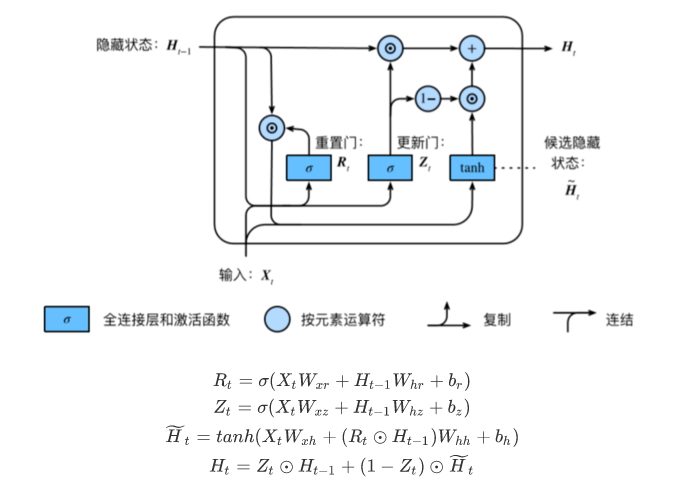重置门有助于捕捉时间序列里短期的依赖关系
更新门有助于捕捉时间序列里长期的依赖关系
import package
mport os
os.listdir('/home/yuzhu/PycharmProjects/deep_learning/Language_model')
import numpy as np
import torch
import torch.nn as nn
import torch.optim
import torch.nn.functional as F
import sys
sys.path.append('/home/yuzhu/PycharmProjects/deep_learning/Language_model')
import language_model_datasets as d2l
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
(corpus_indices, char_to_idx, idx_to_char, vocab_size) = d2l.load_data_lyrics()
Initialize the Parameters
num_inputs, num_hiddens, num_outputs = vocab_size, 256, vocab_size
print('will use', device)
def get_params():
def _one(shape):
ts = torch.tensor(np.random.normal(0, 0.01, size=shape), device=device, dtype=torch.float32)
return torch.nn.Parameter(ts, requires_grad=True)
def _three():
return _one((num_inputs, num_hiddens)), _one((num_hiddens, num_hiddens)), torch.nn.Parameter(
torch.zeros(num_hiddens, device=device, dtype=torch.float32), requires_grad=True)
W_xz, W_hz, b_z = _three()
W_xr, W_hr, b_r = _three()
W_xh, W_hh, b_z = _three()
# the Parameters of the output door
W_hq = _one((num_hiddens, num_outputs))
b_hq = torch.nn.Parameter(torch.zeros(num_outputs, device=device, dtype=torch.float32), requires_grad=True)
return nn.ParameterList([W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q])
def init_gru_state(batch_size, num_hiddens, device):
return torch.zeros((batch_size, num_hiddens), device=device)
GRU model
def gru(inputs, state, params):
W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = params
H, = state
outputs = []
for X in inputs:
Z = torch.sigmoid(torch.matmul(X, W_xz) + torch.matmul(H, W_hz) + b_z)
R = torch.sigmoid(torch.matmul(X, W_xr) + torch.matmul(H, W_hr) + b_r)
H_tilda = torch.tanh(torch.matmul(X, W_xh) + R * torch.matmul(H, W_hz) + b_h)
H = Z * H + (1 - Z) * H_tilda
Y = torch.matmul(H, W_hq) + b_q
outputs.append(Y)
return outputs, (H,)
Training Model
num_epochs, num_steps, batch_size, lr, clipping_theta = 160, 35, 32, 1e2, 1e-2
pred_period, pred_len, prefixes = 40, 50, ['分开', '不分开']
d2l.train_and_predict_rnn(gru, get_params, init_gru_state, num_hiddens,
vocab_size, device, corpus_indices, idx_to_char,
char_to_idx, False, num_epochs, num_steps, lr,
clipping_theta, batch_size, pred_period, pred_len,
prefixes)
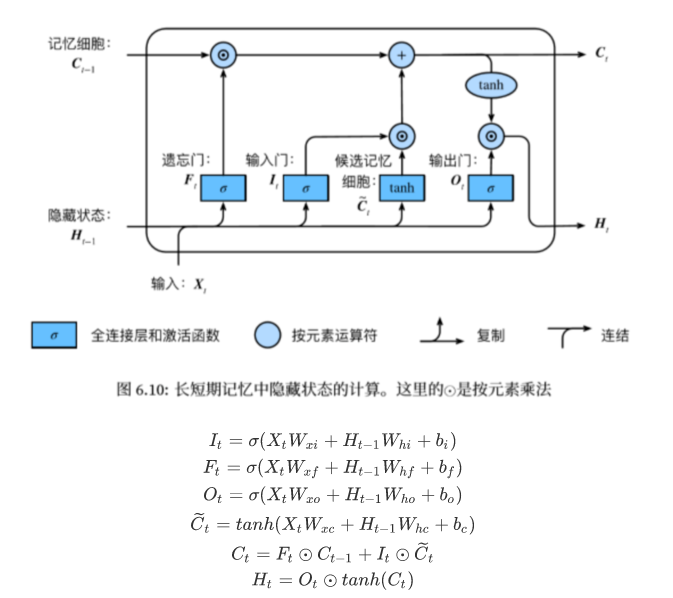
·LSTM-长短期记忆
遗忘门：控制上一时间步的记忆细胞输入门：控制当前时间步的输入
输出门：控制从记忆细胞到隐藏状态
记忆细胞：一种特殊的隐藏状态的信息的流动
Initialize the Parameters
num_inputs, num_hiddens, num_outputs = vocab_size, 256, vocab_size
print('will use', device)
def get_params():
def _one(shape):
ts = torch.tensor(np.random.normal(0, 0.01, size=shape), device=device, dtype=torch.float32)
return torch.nn.Parameter(ts, requires_grad=True)
def _three():
return (_one((num_inputs, num_hiddens)),
_one((num_hiddens, num_hiddens)),
torch.nn.Parameter(torch.zeros(num_hiddens, device=device, dtype=torch.float32), requires_grad=True))
W_xi, W_hi, b_i = _three() # 输入门参数
W_xf, W_hf, b_f = _three() # 遗忘门参数
W_xo, W_ho, b_o = _three() # 输出门参数
W_xc, W_hc, b_c = _three() # 候选记忆细胞参数
# 输出层参数
W_hq = _one((num_hiddens, num_outputs))
b_q = torch.nn.Parameter(torch.zeros(num_outputs, device=device, dtype=torch.float32), requires_grad=True)
return nn.ParameterList([W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c, W_hq, b_q])
def init_lstm_state(batch_size, num_hiddens, device):
return (torch.zeros((batch_size, num_hiddens), device=device),
torch.zeros((batch_size, num_hiddens), device=device))
LSTM Model
def lstm(inputs, state, params):
[W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c, W_hq, b_q] = params
(H, C) = state
outputs = []
for X in inputs:
I = torch.sigmoid(torch.matmul(X, W_xi) + torch.matmul(H, W_hi) + b_i)
F = torch.sigmoid(torch.matmul(X, W_xf) + torch.matmul(H, W_hf) + b_f)
O = torch.sigmoid(torch.matmul(X, W_xo) + torch.matmul(H, W_ho) + b_o)
C_tilda = torch.tanh(torch.matmul(X, W_xc) + torch.matmul(H, W_hc) + b_c)
C = F * C + I * C_tilda
H = O * C.tanh()
Y = torch.matmul(H, W_hq) + b_q
outputs.append(Y)
return outputs, (H, C)
Training Model
num_epochs, num_steps, batch_size, lr, clipping_theta = 160, 35, 32, 1e2, 1e-2
pred_period, pred_len, prefixes = 40, 50, ['分开', '不分开']
d2l.train_and_predict_rnn(lstm, get_params, init_lstm_state, num_hiddens,
vocab_size, device, corpus_indices, idx_to_char,
char_to_idx, False, num_epochs, num_steps, lr,
clipping_theta, batch_size, pred_period, pred_len,
prefixes)
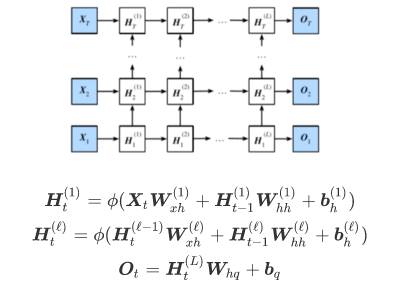
·深度循环神经网络
作者：yonki_e
