POJ - 1163(The Triangle)

Haile ·

更新时间:2024-11-14

· 608 次阅读

题目大意

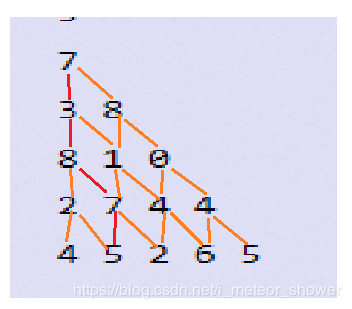
题目大意与下题描述相同在这里插入图片描述

解题思路

在这里插入图片描述
题目描述每次只能移动到下一层的相邻位置，即共有如上图这些路径。不难发现，对于第(i, j)位置来说，只能由(i-1, j-1)或(i-1, j)位置移动而来，即求移动到(i, j)位置的最大数字和时，只能从上述两个位置中选取最大值。即dp[i][j] = max(dp[i-1][j-1], dp[i-1][j]) + value(dp[i][j]dp[i][j]表示走到(i,j)位置的最大和，value表示(i,j)位置的元素值)。

#include 
#include 
#include 
using namespace std;
int value[105][105];    //保存数字三角形
int dp[105][105];   //dp[i][j]表示走到(i,j)位置的最大和
int main() {
    int n;
    while(cin >> n) {
        memset(dp, 0, sizeof(dp));
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j > value[i][j];
            }
        }
        //求dp[i][j]
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= i; j++) {
                dp[i][j] = max(dp[i-1][j], dp[i-1][j-1]) + value[i][j];
            }
        } 
        //求最后一行最大和
        int res = -1;
        for(int i = 1; i <= n; i++) {
            res = max(res, dp[n][i]);
        }
        cout << res << endl;
    }
    return 0;
}

自低向上

对于上述代码和思路我们是按照自顶向下的方向计算的，所以当移动到最后一行时，还需要从最后一行中选择最大和。但是，可以发现不管是自顶向下还是自底向上，可移动的每条路径是保持不变的。而对于自底向上，路径汇集到了一点，省去了最后寻找最大和的一步。状态转移方程式变为了dp[i][j] = max(dp[i+1][j], dp[i+1][j+1]) + value(dp[i][j]dp[i][j]表示走到(i,j)位置的最大和，value表示(i,j)位置的元素值)。

#include 
#include 
#include 
using namespace std;
int value[105][105];    //保存数字三角形
int dp[105][105];   //dp[i][j]表示走到(i,j)位置的最大和
int main() {
    int n;
    while(cin >> n) {
        memset(dp, 0, sizeof(dp));
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j > value[i][j];
            }
        }
        //求dp[i][j]
        for(int i = n; i >= 1; i--) {
            for(int j = 0; j <= i; j++) {
                dp[i][j] = max(dp[i+1][j], dp[i+1][j+1]) + value[i][j];
            }
        }
        cout << dp[1][1] << endl;
    }
    return 0;
}

优化空间复杂度

dp[i][j] = max(dp[i+1][j], dp[i+1][j+1]) + value(dp[i][j]dp[i][j]表示走到(i,j)位置的最大和，value表示(i,j)位置的元素值)。

观察这个动态转移方程式，可以看出计算第i层的最大和时，只需要借助i+1层计算出的最大和，而对于i层以前保存最大和的空间都是不需要的(dp[0~i][j])。所以，可以省去一维空间，用dp[i]表示走到i位置的最大和,外层循环控制层数。即dp[j] = max(dp[j], dp[j+1]) + value[i][j](自底向上)。但需要注意的时内层循环的方向，对于自底向上计算案例，需要用到上一层的j和j+1位置上的最大和，所以为了不影响后续计算，j循环次序应为1~i，而自顶向下相反。

#include 
#include 
#include 
using namespace std;
int value[105][105];    //保存数字三角形
int dp[105];   //dp[i]表示走到i位置的最大和,外层循环控制层数
int main() {
    int n;
    while(cin >> n) {
        memset(dp, 0, sizeof(dp));
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j > value[i][j];
            }
        for(int i = n; i >= 1; i--) {	
            for(int j = 0; j <= i; j++) {	//注意循环次序
                dp[j] = max(dp[j], dp[j+1]) + value[i][j];
            }
        }
        cout << dp[1] << endl;
    }
    return 0;
}

作者：i_meteor_shower

poj triangle

1024 个赞