通俗易懂！视觉slam第五部分——slam数学表示二

假设我们进行了两次变换：, 和 , ，满足：

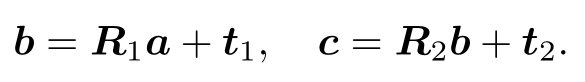
但是从 a 到 c 的变换为：

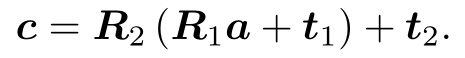
这样的形式在变换多次之后会过于复杂。因此，我们要引入齐次坐标和变换矩阵重写:

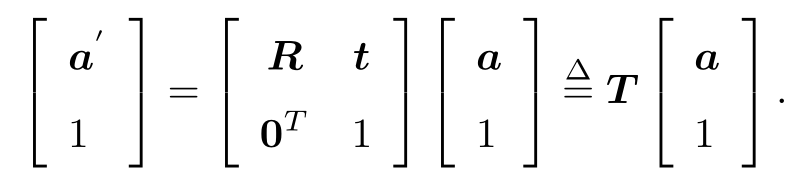
这是一个数学技巧：我们把一个三维向量的末尾添加 1，变成了四维向量，称为齐次坐标。对于这个四维向量，我们可以把旋转和平移写在一个矩阵里面，使得整个关系变成了线性关系。该式中，矩阵 T 称为变换矩阵（Transform Matrix）。我们暂时用 ˜ a 表示 a 的齐次坐标。 

齐次坐标是射影几何里的概念。通过添加最后一维，我们用四个实数描述了一个三维向量，这显然多了一个自由度，但允许我们把变换写成线性的形式。在齐次坐标中，某个点 x 的每个分量同乘一个非零常数 k 后，仍然表示的是同一个点。因此，一个点的具体坐标值不是唯一的。如 [1,1,1,1] T 和 [2,2,2,2] T 是同一个点。但当最后一项不为零时，我们总可以把所有坐标除以最后一项，强制最后一项为 1，从而得到一个点唯一的坐标表示（也就是转换成非齐次坐标）：

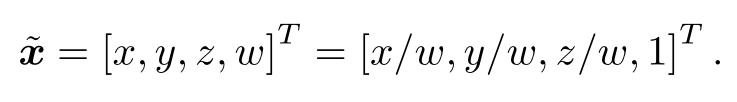
这时，忽略掉最后一项，这个点的坐标和欧氏空间就是一样的。依靠齐次坐标和变换矩阵，两次变换的累加就可以有很好的形式： 

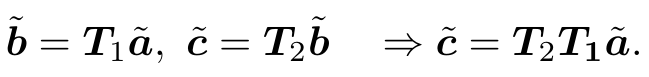
关于变换矩阵 T，它具有比较特别的结构：左上角为旋转矩阵，右侧为平移向量，左下角为 0 向量，右下角为 1。这种矩阵又称为特殊欧氏群（Special Euclidean Group）： 

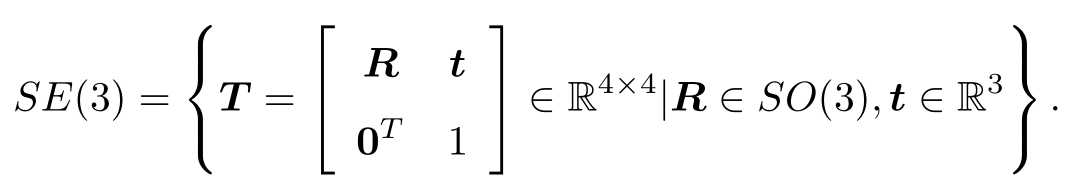
 与 SO(3) 一样，求解该矩阵的逆表示一个反向的变换

slam