通俗易懂！视觉slam第三部分——slam数学表示

用数学语言来描述 SLAM 过程。我们会用到一些变量和公式。

小车正携带着某种传感器在未知环境里运动，怎么用数学语言描述这件事呢？
首先，由于相机通常是在某些时刻采集数据的，所以我们也只关心这些时刻的位置和地图。这就把一段连续时间的运动变成了离散时刻 t = 1,...,K 当中发生的事情。在这些时刻，用 x 表示小车自身的位置。于是各时刻的位置就记为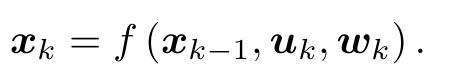

这里  是运动传感器的读数（有时也叫输入），为噪声。注意到，我们用一个一般函数 f 来描述这个过程，而不具体指明 f 的作用方式。这使得整个函数可以指代任意的运动传感器，成为一个通用的方程，而不必限定于某个特殊的传感器上。我们把它称为运动方程。 

与运动方程相对应，还有一个观测方程。观测方程描述的是，当小萝卜在位置上看到某个路标点，产生了一个观测数据。同样，我们用一个抽象的函数 h 来描述这个关系：

 这里 v k,j 是这次观测里的噪声。由于观测所用的传感器形式更多，这里的观测数据 z以及观测方程 h 也许多不同的形式。

根据小车的真实运动和传感器的种类，存在着若干种参数化方式（Parameterization）。假设小萝卜在平面中运动，那么，它的位姿 x 由两个位置和一个转角来描述，即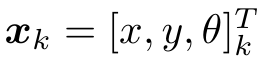 。同时，运动传感器能够测量到小萝卜在每两个时间间隔位置和转角的变化量 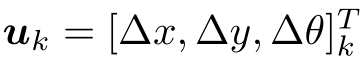，那么，此时运动方程就可以具体化为：

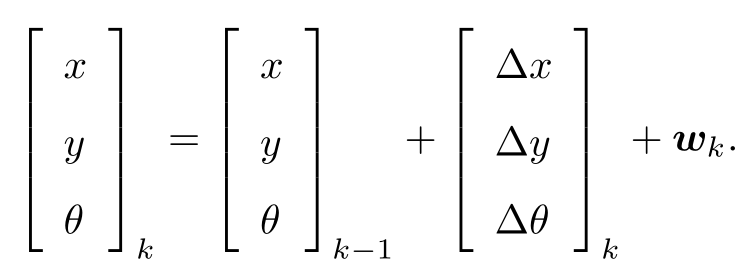
这是简单的线性关系。不过，并不是所有的传感器都直接能测量出位移和角度变化，所以也存在着其他形式更加复杂的运动方程，那时我们可能需要进行动力学分析。关于观测方程，比方说小萝卜携带着一个二维激光传感器。我们知道激光传感器观测一个 2D 路标点时，能够测到两个量：路标点与小萝卜本体之间的距离 r 和夹角 ϕ。我们记路标点为 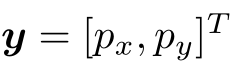（为保持简洁，省略了下标），观测数据为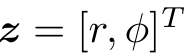，那么观测方程就具体化为：

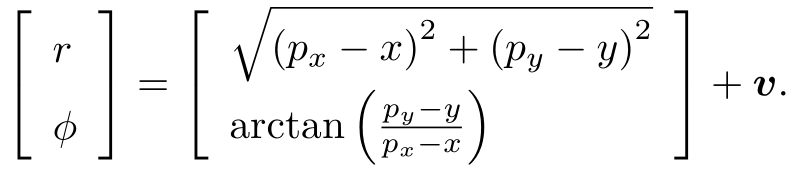
可见，针对不同的传感器，这两个方程有不同的参数化形式。如果我们保持通用性，把它们取成通用的抽象形式，那么 SLAM 过程可总结为两个基本方程： 

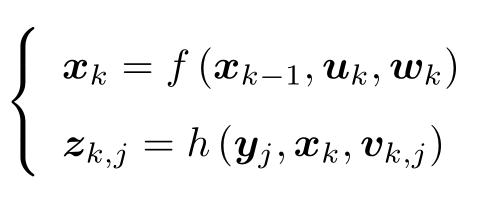
 状态估计问题的求解，与两个方程的具体形式，以及噪声服从哪种分布有关。我们按照运动和观测方程是否为线性，噪声是否服从高斯分布进行分类，分为线性/非线性和高斯/非高斯系统。其中线性高斯系统（Linear Gaussian, LG 系统）是最简单的，它的无偏的最优估计可以由卡尔曼滤波器（Kalman Filter, KF）给出。而在复杂的非线性非高斯系统（Non-Linear Non-Gaussian，NLNG 系统）中，我们会使用以扩展卡尔曼滤波器（ExtendedKalman Filter, EKF）和非线性优化两大类方法去求解它。

slam