2020美赛数学建模校级培训——Week_2

Aurora ·

更新时间:2024-11-14

· 632 次阅读

引言：

博主在今年寒假参加了学校组织的美国大学生数学建模竞赛培训，在此，用博客来记录这段培训时光。

本篇博客将记录第二轮培训（1.9——1. 13）的相关培训内容：
在这里插入图片描述

Day 6: 2020.1.9 一、排队论模型 1. 基本概念：

排队论（ queuing), 也称随机服务系统理论，是运筹学的一个主要分支。

1909年，丹麦哥本哈根电子公司电话工程师 A. K. Erlang的开创性论文“概率论和电话通讯理论” 标志此理论的诞生。
排队论的发展最早是与电话，通信中的问题相联系的，并到现在是排队论的传统的应用领域。近年来在计算机通讯网络系统、交通运输、
医疗卫生系统、库存管理、作战指挥等各领域中均得到应用。
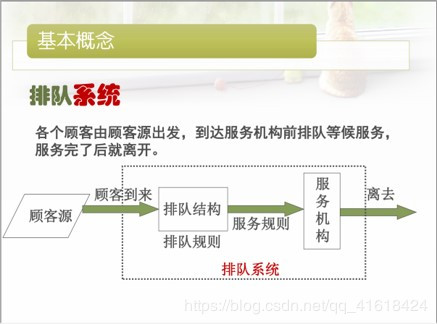
在这里插入图片描述

2. 输入过程：

（1）顾客源的组成有限的无限的**

（ 2）顾客到来的方式一个一个的成批的

（ 3）顾客相继到达的间隔时间确定型的随机型的

（ 4）顾客的到来相互独立的关联的

（ 5）输入过程平稳的（不受时间影响），非平稳的（复杂)

3. 排队规则

顾客在排队系统中按怎样的规则、次序接受服务的。

（ 1）顾客到达时，所有服务台被占用随即离去的称为即时制（损失制）

排队等候称为等待制：

先到先服务后到先服务随机服务有优先权

（ 2）从队列占用空间:

有限的无限的

（ 3）从队列的数量 :

单列多列（假设排队过程中不允许转移或退出） 4. 排队模型的分类：

在这里插入图片描述

5. 排队模型的参数

1、队长Ls：指在系统中的顾客数。

2、排队长Lq：指系统中排队等候服务的顾客数。

Ls=Lq+正被服务的顾客数

3、逗留时间Ws：指一个顾客在系统中的停留时间。

4、等待时间Wq：指一个顾客在系统中排队等待的时间。

Ws=Wq+服务时间

5、忙期：指从顾客到达空闲服务机构起到服务机构再次空闲止，这段时间长度，即服务机构连续繁忙的时间长度。

6、系统的状态概率Pn( t ) ：指系统中的顾客数为n的概率。

7、稳定状态： limPn(t)→Pn

6. 时间分布

在这里插入图片描述

Day 7: 2020.1.10 一、排队模型仿真实验 1. 产生随机数的MATLAB命令：

1.unifrnd(a,b,m,n): 产生m× n阶[a, b]上服从均匀分布U(a, b)的随机数矩阵。

2.rand (m, n): 产生m× n阶[0,1]上服从均匀分布的随机数矩阵。

3.exprnd (,m, n)：产生m× n阶期望为的服从指数分布的随机数矩阵。

4 poissrnd (,m, n)：产生m× n阶参数为的服从泊松分布的随机数矩阵。

2. 单服务台的排队模型：

在某商店有一个售货员，顾客陆续来到，售货员逐个地接待顾客．当到来的顾客较多时，一部分顾客便须排队等待，被接待后的顾客便离开商店．设：

1．顾客到来间隔时间服从参数为0.1的指数分布．

2．对顾客的服务时间服从[4,15]上的均匀分布．

3．排队按先到先服务规则，队长无限制．

假定一个工作日为8小时，时间以分钟为单位．

问题1. 模拟一个工作日内完成服务的个数及顾客平均等待时

间t？

问题2. 模拟100个工作日，求出平均每日完成服务的个数及

每日顾客的平均等待时间？

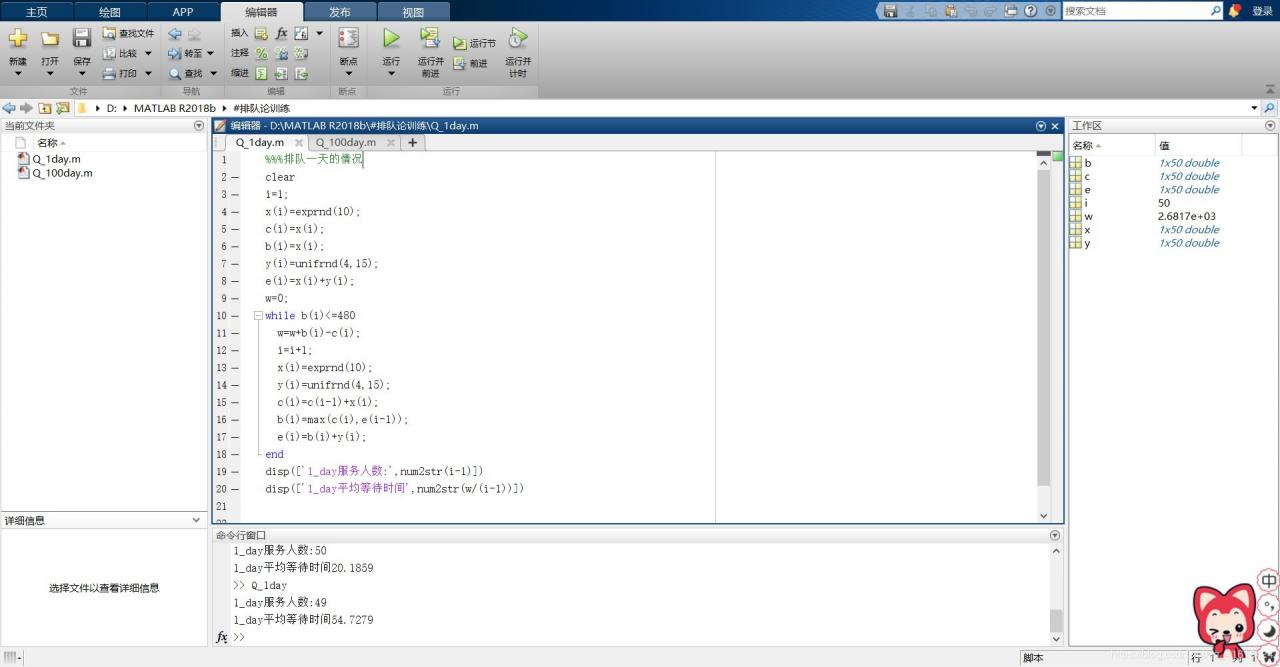
3. MATLAB编程

1_day:

%%%排队一天的情况
clc clear all;
i=1;
x(i)=exprnd(10);
c(i)=x(i);
b(i)=x(i);
y(i)=unifrnd(4,15); 
e(i)=x(i)+y(i);
w=0;
while b(i)<=480
  w=w+b(i)-c(i); 
  i=i+1;
  x(i)=exprnd(10); 
  y(i)=unifrnd(4,15); 
  c(i)=c(i-1)+x(i);   
  b(i)=max(c(i),e(i-1)); 
  e(i)=b(i)+y(i);   
end
disp([&apos;服务人数&apos;,num2str(i-1)])
disp([&apos;平均等待时间&apos;,num2str(w/(i-1))])

100_day：

%%%排队N天的情况
clc clear all;
N=100;
I=0; %100天总服务人数
W=0; %100天总等待时间
for k=1:N
i=1;
x(i)=exprnd(10);
c(i)=x(i);
b(i)=x(i);
y(i)=unifrnd(4,15); 
e(i)=x(i)+y(i);
w=0;
while b(i)<=480
  w=w+b(i)-c(i);  
  i=i+1;
  x(i)=exprnd(10); 
  y(i)=unifrnd(4,15); 
  c(i)=c(i-1)+x(i);   
  b(i)=max(c(i),e(i-1)); 
  e(i)=b(i)+y(i);   
end
I=I+i-1;
W=W+w/(i-1);
end
disp([&apos;服务人数&apos;,num2str(I/N)])
disp([&apos;平均等待时间&apos;,num2str(W/N)])

在这里插入图片描述

Day 8: 2020.1.11 第二轮模拟题：2018 MCM_C 1. Problem

2018 MCM C 题：生产能源

背景：能源生产和使用是任何经济的重要组成部分。在美国，能源政策的许多方面都分散下放到州的水平。此外，不同州的地理区域和工业影响能源的使用和生产。在

1970 年，12
个在美国西方的州形成西部州际能源协议（WIEC），其任务重点是促进这些州之间的合作，促进发展和核能技术管理。州际契约是一种在两个或多个州之间的契约安排。在这些州就具体的政策问题达成一致意见，就某一特定的区域或州事项采取一套标准或相互合作。

问题：在美国与墨西哥的边境，有四个州—美国加利福尼亚州（CA），亚利桑那州（AZ），美国新墨西哥州（NM）和得克萨斯州（TX），这是希望到形成一个关注增加使用清洁、可再生能源的来源的实际的新能源契约。你的团队需要帮助这四个州的州长对这些数据进行分析和建模，然后通知他们制定一系列发展他们的州际能源契约的目标。

该附件数据文件“ProblemCData.xlsx”提供的第一个工作簿（“seseds ”）是 50 年中四个州的能源生产和消费数据的
605 个变量，伴随一些人口和经济信息。在这个数据集中，605 个变量的名称被定义在第二工作簿（“msncodes”）中。

l 第一部分：

A.使用所提供的数据，为这四个州分别创建一个能量概况。

B.建立一个模型来描述从

1960 到 2009
年这四个州的能量是如何演化的。分析和解释模型的结果，以解决四个州使用清洁和可再生能源的问题，用州长们很容易理解的方式，帮助他们了解四个州之间的异同。你的讨论包括可能影响异同的的因素（例如地理，工业、人口和气候）。

C.确定在 2009 年这四个州中哪一个州有“最佳”使用清洁和可再生能源的概况。解释你的标准和选择。

D.基于这些州使用能源的历史演变，以及你对所建立的州概况之间差异的理解，如你所定义的那样，在每个州长办公室没有任何政策改变的情况下，分别预测

2025 和 2050 年每个州的能源概况。

l 第二部分：

A.基于你对这四个州的比较，用你的“最佳”概况的标准和你的预测，来确定 2025 和 2050
年的可再生能源使用的目标，并将它们作为新的四州能量契约的目标。

B.确定并讨论四个州可能采取的至少三项行动，以实现他们能源紧缩契约目标。

l 第三部分：