MPC初学2（数学建模）

模型预测控制系统是基于数学建模，这种模型被称为状态-空间模型。通过状态-空间模型，能用当前的状态变量和操纵变量（偏差值）来表示未来状态量。
接下里我们举一个单输入-单输出的例子,它可以被如下描述：
xm(k+1)=Amxm(k)+Bmu(k) ①;
y(k)=Cmxm(k) ② ;
其中u(k)是操纵变量，作为输入；xm(k)是当前状态变量，作为输入；y(k)为输出变量；Am,Bm,Cm分别为关系矩阵。
接下来我们对①式求偏差，得：
xm(k+1)-xm(k)=Am（xm(k)+xm(k-1)）+Bm（u(k)-u(k-1)）；
其中计 Δxm(k+1)=xm(k+1)-xm(k)；Δxm(k)=xm(k)-xm(k-1)；Δu(k)=u(k)-u(k-1)
通过简单变形可得状态-空间方程为：
Δxm(k+1)=AmΔxm(k)+BmΔu(k) ③
到现在我们建模已经完成了的一大半，接下来需要将Δxm(k)与输出y(k)联系起来。
对②式求偏差，得：
y(k+1)-y(k)=Cm(xm(k+1)-xm(k))=CmΔxm(k+1)=CmAmΔxm(k)+CmBmΔu(k). ④
接下来我们令一个新的状态变量矩阵：
并将③、④用矩阵形式表示：

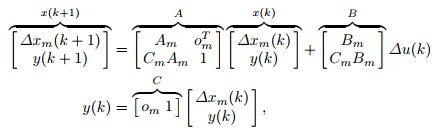
至此,状态-空间模型建立完毕：
x(k+1)=Ax(k)+BΔu(k);
y(k)=[0m 1]x(k)
其中0m=[0 0 …0]

数学建模 数学