统计建模与R软件——书籍问题

Eirene ·

更新时间:2024-09-21

· 875 次阅读

望知道出错原因的同学能够解答本人的疑惑，谢谢！
Traumereiisun @_@

第三章数据描述性分析

p127

如果 x 是数据框，则 mean() 的返回值就是向量，如
mean(as.data.frame(x))
V1 V2 V3 V4
2 5 8 11

本人实践：

> x<-1:12;dim(x) x;mean(x);as.data.frame(x);mean(as.data.frame(x))
     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    2    5    8   11
[3,]    3    6    9   12
[1] 6.5
  V1 V2 V3 V4
1  1  4  7 10
2  2  5  8 11
3  3  6  9 12
[1] NA
Warning message:
In mean.default(as.data.frame(x)) : 参数不是数值也不是逻辑值：回覆NA

p128
该页的 weighted.mean() 函数也出现类似问题

p141

样本的偏度系数（记为g1）" src="/upload/wp-content/uploads/2020/02/20200219175958171.png">

如偏度小于0，直方图偏右等.

偏度：
（1）正态分布（偏度 = 0）
算术平均值 = 中位数 = 众数，

（2）右偏分布，右边的尾部相对于与左边的尾部要长
（也叫正偏分布，其偏度 > 0）
众数 < 中位数 < 算术平均值
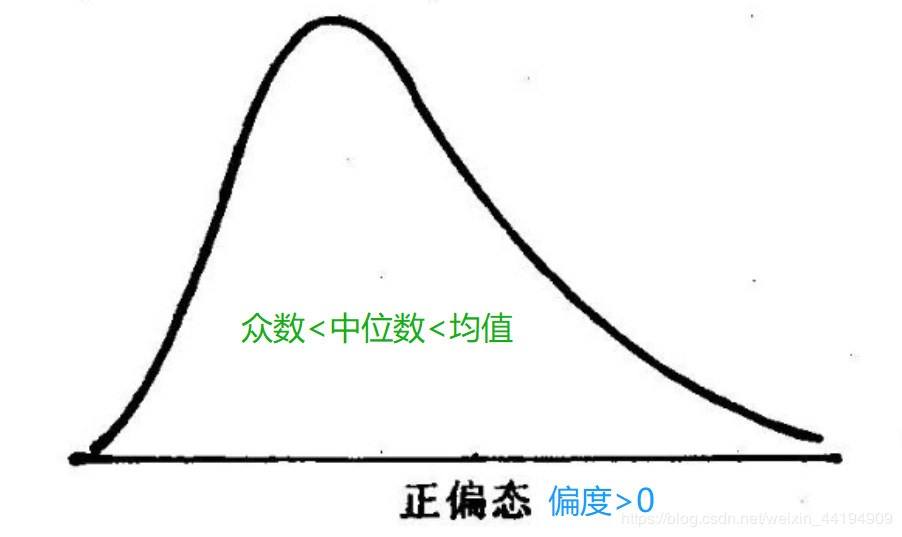
在这里插入图片描述

由偏度的公式可知，影响偏度正负取值的主要因素是红色方框。已知“右偏：众数 0 ？

我与左同学的讨论结果：
（不够精确，待大神指点）
假设左边的样本多于右边的样本。
左边：（xi-xbar）< 0，3次方与sum导致负数越来越负；
右边：因为右边尾巴很长，所以（xi-xbar）的3次方远远 > 0，sum导致正数越来越正
最终，尽管左边的样本多于右边的样本，但是，左右相抵，右边胜出！

（3）左偏分布，左边的尾部相对于与右边的尾部要长
（也叫负偏分布，其偏度 < 0）
算术平均值 < 中位数 < 众数
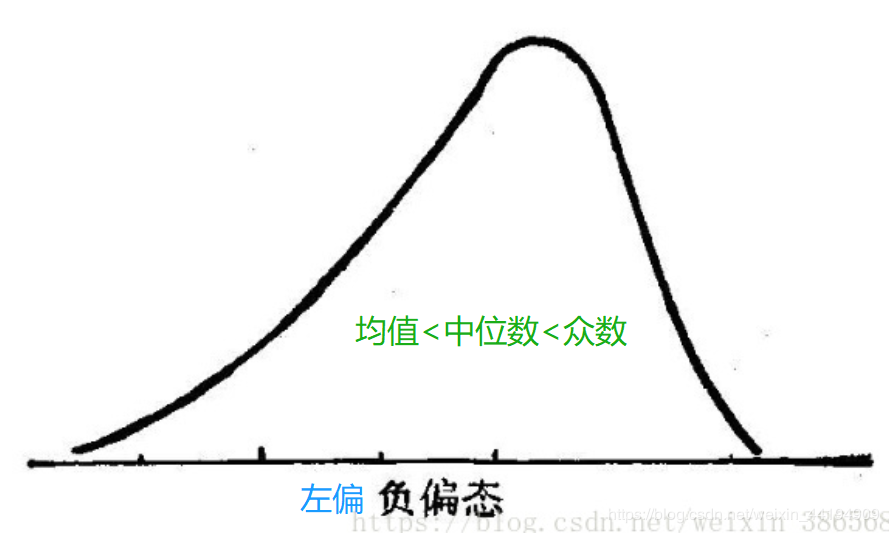
在这里插入图片描述

同理，为什么左偏的结果是偏度 0啊！

p145

scale = 2，即将10个个位数分成两段，0 ~ 4 为一段，5 ~ 9 为另一段
如果选择 scale = 1/2，即将 10 个个位数分成 1/2 段，即 20 个数一段？？？

> x length(x)
[1] 31
> stem(x)
  The decimal point is 1 digit(s) to the right of the |
   2 | 5
   3 | 
   4 | 5
   5 | 045
   6 | 148
   7 | 25589
   8 | 1344456667999
   9 | 0112
  10 | 0
> stem(x,scale=2)
  The decimal point is 1 digit(s) to the right of the |
   2 | 5
   3 | 
   3 | 
   4 | 
   4 | 5
   5 | 04
   5 | 5
   6 | 14
   6 | 8
   7 | 2
   7 | 5589
   8 | 13444
   8 | 56667999
   9 | 0112
   9 | 
  10 | 0
> stem(x,scale=0.5)
  The decimal point is 1 digit(s) to the right of the |
   2 | 5
   4 | 5045
   6 | 14825589
   8 | 13444566679990112
  10 | 0

p149
对箱线图的理解记忆：

四分位距，即 IQR = Q3 - Q1
Q3: 75%分位数
Q1: 25%分位数 , Q3和Q1为四分位数
50% 的数据集中于箱体内。若箱体太大，即数据分布离散，数据波动较大；箱体小表示数据集中。箱子的上边为上四分位数Q3，下边为下四分位数Q1，箱体中的横线为中位数Q2（50%分位数）箱子的上触须为数据的最大值Max，下触须为数据的最小值Min（注意是非离群点的最大最小值，称为上下相邻值）若数据值 > Q3 + 1.5 IQR（上限值）或数据值 Q3 + 3 IQR 或数据值 < Q1 - 3 IQR ,均视为极值。在实际应用中，不会显示异常值与极值的界限，而且一般统称为异常值。

图形记忆：
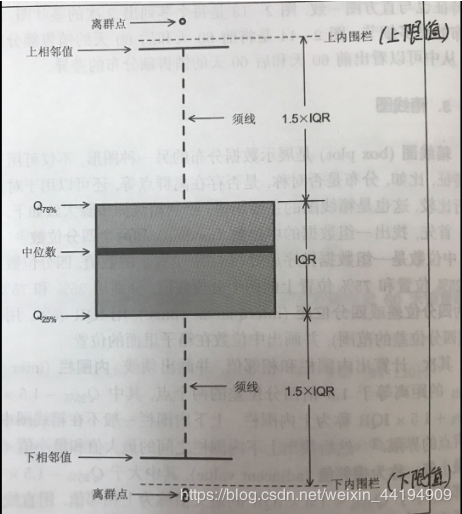
在这里插入图片描述
图片参考网址

p149
箱线图带有切口，但是，不知道黑圈圈圈出的地方代表什么？
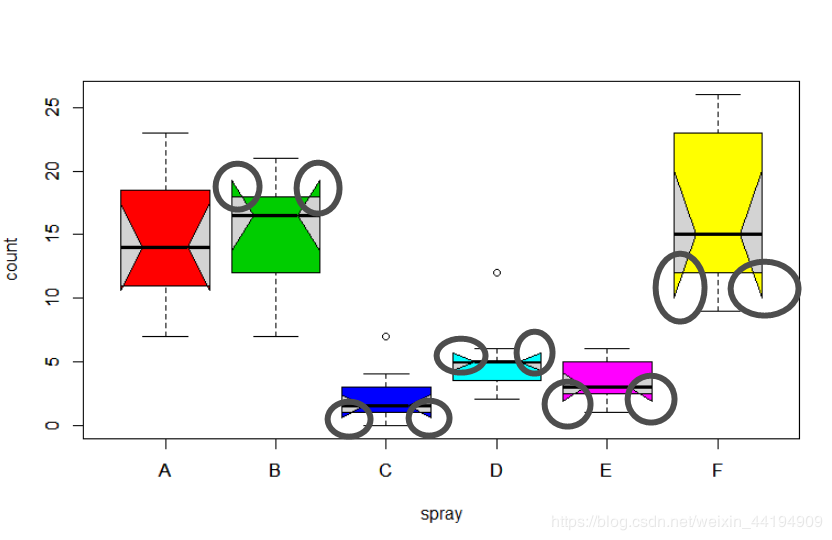
在这里插入图片描述

> boxplot(count~spray,data=InsectSprays,col="lightgray")
> boxplot(count~spray,data=InsectSprays,notch=TRUE,col=2:7,add=TRUE)
Warning message:
In bxp(list(stats = c(7, 11, 14, 18.5, 23, 7, 12, 16.5, 18, 21,  :
  一些槽在折叶点外('box'): 可能是因为notch=FALSE

p151
1. 正态性W检验方法

函数 shapiro.test() 提供 W 统计量和相应的 p 值，当p 值小于某个显著性水平 α\alphaα（比如 0.05），则认为样本为不是来自正态分布的总体；否则承认样本来自正态分布的总体。

eg 1:

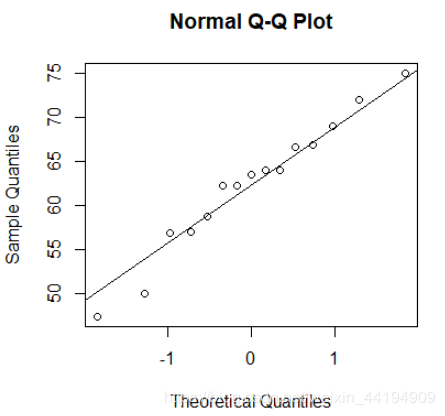
> w
 [1] 75.0 64.0 47.4 66.9 62.2 62.2 58.7
 [8] 63.5 66.6 64.0 57.0 69.0 56.9 50.0
[15] 72.0
> shapiro.test(w)
	Shapiro-Wilk normality test
data:  w
W = 0.96862, p-value = 0.8371

p 值 = 0.8371 > 0.05，认为来自正态分布的总体，与 QQ 图得到的结论相同。

> qqnorm(w);qqline(w)

在这里插入图片描述
eg 2:

> shapiro.test(runif(100,min=2,max=4))
	Shapiro-Wilk normality test
data:  runif(100, min = 2, max = 4)
W = 0.94089, p-value = 0.0002185

p 值 = 0.0002185 < 0.05，认为样本不是来自正态分布的总体。当然，这是来自均匀分布的随机数。

**2. 经验分布的 Kolmogorov-Smirnov 检验方法 **

经验分布拟合检验的方法是检验经验分布函数 Fn(x)F_n(x)Fn(x) 与假设的总体分布函数 F0(x)F_0(x)F0(x) 之间的差异。
统计量是计算 Fn(x)F_n(x)Fn(x) 与 F0(x)F_0(x)F0(x) 之间的距离 DDD：
D=sup−∞<x<∞∣Fn(x)−F0(x)∣D=sup_{-\infty<x<\infty}|F_n(x)-F_0(x)|D=sup−∞<x<∞∣Fn(x)−F0(x)∣

> x 
> # 认为样本是来自总体为F(2,5)分布
> ks.test(x,"pf",2,5)
	One-sample Kolmogorov-Smirnov
	test
data:  x
D = 0.49, p-value < 2.2e-16
alternative hypothesis: two-sided

结果拒绝，即不认为 xxx 服从 F2,5F_{2,5}F2,5 分布

作者：小太阳Devil

书籍

1024 个赞