神经网络的前向传播和反向传播推导

Ines ·

更新时间:2024-09-21

· 636 次阅读

神经网络的前向传播和反向传播推导

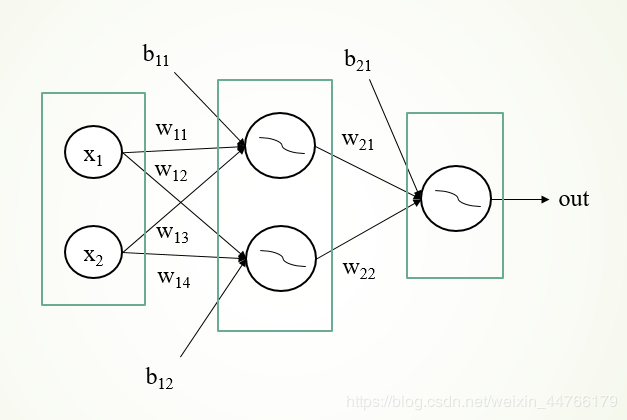
在这里插入图片描述
x1x_{1}x1和x2x_{2}x2表示输入
wijw_{ij}wij表示权重
bijb_{ij}bij表示偏置
σi\sigma_{i}σi表示激活函数，这里使用sigmoid激活函数
outoutout表示输出
yyy表示真实值
η\etaη表示学习率

前向传播
h1=w11x1+w13x2+b11h_{1}=w_{11}x_{1}+w_{13}x_{2}+b_{11}h1=w11x1+w13x2+b11，α1=σ(h1)=11+e−h1\alpha_{1}=\sigma(h1)=\frac{1}{1+e^{-h1}}α1=σ(h1)=1+e−h11

h2=w12x1+w14x2+b12h_{2}=w_{12}x_{1}+w_{14}x_{2}+b_{12}h2=w12x1+w14x2+b12，α2=σ(h2)=11+e−h2\alpha_{2}=\sigma(h2)=\frac{1}{1+e^{-h2}}α2=σ(h2)=1+e−h21

z=w21α1+w22α2+b21z=w_{21}\alpha_{1}+w_{22}\alpha_{2}+b_{21}z=w21α1+w22α2+b21，out=σ(z)=11+e−zout=\sigma(z)=\frac{1}{1+e^{-z}}out=σ(z)=1+e−z1

损失函数

E=12(out−y)2E=\frac{1}{2}(out-y)^2E=21(out−y)2

反向传播
求导
△w21=∂E∂w21=∂E∂out∂out∂z∂z∂w21=(out−y)σ(z)(1−σ(z))α1\bigtriangleup w_{21}=\frac{\partial E}{\partial w_{21}}=\frac{\partial E}{\partial out}\frac{{\partial out}}{\partial z}\frac{\partial z}{\partial w_{21}}=(out-y)\sigma(z)(1-\sigma(z))\alpha_{1}△w21=∂w21∂E=∂out∂E∂z∂out∂w21∂z=(out−y)σ(z)(1−σ(z))α1

△w22=∂E∂w22=∂E∂out∂out∂z∂z∂w22=(out−y)σ(z)(1−σ(z))α2\bigtriangleup w_{22}=\frac{\partial E}{\partial w_{22}}=\frac{\partial E}{\partial out}\frac{{\partial out}}{\partial z}\frac{\partial z}{\partial w_{22}}=(out-y)\sigma(z)(1-\sigma(z))\alpha_{2}△w22=∂w22∂E=∂out∂E∂z∂out∂w22∂z=(out−y)σ(z)(1−σ(z))α2

△b21=∂E∂b21=∂E∂out∂out∂z∂z∂b21=(out−y)σ(z)(1−σ(z))\bigtriangleup b_{21}=\frac{\partial E}{\partial b_{21}}=\frac{\partial E}{\partial out}\frac{{\partial out}}{\partial z}\frac{\partial z}{\partial b_{21}}=(out-y)\sigma(z)(1-\sigma(z))△b21=∂b21∂E=∂out∂E∂z∂out∂b21∂z=(out−y)σ(z)(1−σ(z))

更新w21、w22、b21w_{21}、w_{22}、b_{21}w21、w22、b21

w21=w21−η△w21w_{21}=w_{21}-\eta \bigtriangleup w_{21}w21=w21−η△w21

w22=w22−η△w22w_{22}=w_{22}-\eta \bigtriangleup w_{22}w22=w22−η△w22

b21=b21−η△b21b_{21}=b_{21}-\eta \bigtriangleup b_{21}b21=b21−η△b21

求导

△w12=∂E∂out∂out∂z∂z∂α2∂α2∂h2∂α2∂h2∂h2∂w12=(out−y)σ(z)(1−σ(z))w22σ(h2)(1−σ(h2))x1\bigtriangleup w_{12}=\frac{\partial E}{\partial out}\frac{\partial out}{\partial z}\frac{\partial z}{\partial \alpha_{2}}\frac{\partial \alpha_{2}}{\partial h2}\frac{\partial \alpha_{2}}{\partial h_{2}}\frac{{\partial h_{2}}}{\partial w_{12}} =(out-y)\sigma(z)(1-\sigma(z))w_{22}\sigma(h_{2})(1-\sigma(h_{2}))x_{1}△w12=∂out∂E∂z∂out∂α2∂z∂h2∂α2∂h2∂α2∂w12∂h2=(out−y)σ(z)(1−σ(z))w22σ(h2)(1−σ(h2))x1

△w14=∂E∂out∂out∂z∂z∂α2∂α2∂h2∂α2∂h2∂h2∂w14=(out−y)σ(z)(1−σ(z))w22σ(h2)(1−σ(h2))x2\bigtriangleup w_{14}=\frac{\partial E}{\partial out}\frac{\partial out}{\partial z}\frac{\partial z}{\partial \alpha_{2}}\frac{\partial \alpha_{2}}{\partial h2}\frac{\partial \alpha_{2}}{\partial h_{2}}\frac{{\partial h_{2}}}{\partial w_{14}} =(out-y)\sigma(z)(1-\sigma(z))w_{22}\sigma(h_{2})(1-\sigma(h_{2}))x_{2}△w14=∂out∂E∂z∂out∂α2∂z∂h2∂α2∂h2∂α2∂w14∂h2=(out−y)σ(z)(1−σ(z))w22σ(h2)(1−σ(h2))x2

△b12=∂E∂out∂out∂z∂z∂α2∂α2∂h2∂α2∂h2∂h2∂b12=(out−y)σ(z)(1−σ(z))w22σ(h2)(1−σ(h2))\bigtriangleup b_{12}=\frac{\partial E}{\partial out}\frac{\partial out}{\partial z}\frac{\partial z}{\partial \alpha_{2}}\frac{\partial \alpha_{2}}{\partial h2}\frac{\partial \alpha_{2}}{\partial h_{2}}\frac{{\partial h_{2}}}{\partial b_{12}} =(out-y)\sigma(z)(1-\sigma(z))w_{22}\sigma(h_{2})(1-\sigma(h_{2}))△b12=∂out∂E∂z∂out∂α2∂z∂h2∂α2∂h2∂α2∂b12∂h2=(out−y)σ(z)(1−σ(z))w22σ(h2)(1−σ(h2))

△w11=∂E∂out∂out∂z∂z∂α1∂α1∂h1∂α1∂h1∂h1∂w11=(out−y)σ(z)(1−σ(z))w21σ(h1)(1−σ(h1))x1\bigtriangleup w_{11}=\frac{\partial E}{\partial out}\frac{\partial out}{\partial z}\frac{\partial z}{\partial \alpha_{1}}\frac{\partial \alpha_{1}}{\partial h1}\frac{\partial \alpha_{1}}{\partial h_{1}}\frac{{\partial h_{1}}}{\partial w_{11}}=(out-y)\sigma(z)(1-\sigma(z))w_{21}\sigma(h_{1})(1-\sigma(h_{1}))x_{1}△w11=∂out∂E∂z∂out∂α1∂z∂h1∂α1∂h1∂α1∂w11∂h1=(out−y)σ(z)(1−σ(z))w21σ(h1)(1−σ(h1))x1

△w13=∂E∂out∂out∂z∂z∂α1∂α1∂h1∂α1∂h1∂h1∂w13=(out−y)σ(z)(1−σ(z))w21σ(h1)(1−σ(h1))x2\bigtriangleup w_{13}=\frac{\partial E}{\partial out}\frac{\partial out}{\partial z}\frac{\partial z}{\partial \alpha_{1}}\frac{\partial \alpha_{1}}{\partial h1}\frac{\partial \alpha_{1}}{\partial h_{1}}\frac{{\partial h_{1}}}{\partial w_{13}}=(out-y)\sigma(z)(1-\sigma(z))w_{21}\sigma(h_{1})(1-\sigma(h_{1}))x_{2}△w13=∂out∂E∂z∂out∂α1∂z∂h1∂α1∂h1∂α1∂w13∂h1=(out−y)σ(z)(1−σ(z))w21σ(h1)(1−σ(h1))x2

△b11=∂E∂out∂out∂z∂z∂α1∂α1∂h1∂α1∂h1∂h1∂b11=(out−y)σ(z)(1−σ(z))w21σ(h1)(1−σ(h1))\bigtriangleup b_{11}=\frac{\partial E}{\partial out}\frac{\partial out}{\partial z}\frac{\partial z}{\partial \alpha_{1}}\frac{\partial \alpha_{1}}{\partial h1}\frac{\partial \alpha_{1}}{\partial h_{1}}\frac{{\partial h_{1}}}{\partial b_{11}}=(out-y)\sigma(z)(1-\sigma(z))w_{21}\sigma(h_{1})(1-\sigma(h_{1}))△b11=∂out∂E∂z∂out∂α1∂z∂h1∂α1∂h1∂α1∂b11∂h1=(out−y)σ(z)(1−σ(z))w21σ(h1)(1−σ(h1))

更新w12、w14、b12w_{12}、w_{14}、b_{12}w12、w14、b12

w12=w12−η△w12w_{12}=w_{12}-\eta \bigtriangleup w_{12}w12=w12−η△w12

w14=w14−η△w14w_{14}=w_{14}-\eta \bigtriangleup w_{14}w14=w14−η△w14

b12=b12−η△b12b_{12}=b_{12}-\eta \bigtriangleup b_{12}b12=b12−η△b12

更新w11、w13、b11w_{11}、w_{13}、b_{11}w11、w13、b11

w11=w11−η△w11w_{11}=w_{11}-\eta \bigtriangleup w_{11}w11=w11−η△w11

w13=w13−η△w13w_{13}=w_{13}-\eta \bigtriangleup w_{13}w13=w13−η△w13

b11=b11−η△b11b_{11}=b_{11}-\eta \bigtriangleup b_{11}b11=b11−η△b11

import matplotlib.pyplot as plt
import numpy as np
# 定义参数
# N：样本数量
# D_in：数据维度、输入维度
# H：隐藏层神经元个数
# D_out：输出维度
N, D_in, H, D_out = 64, 1000, 100, 10
# 生成数据
x = np.random.randn(D_in, N)
y = np.random.randn(D_out, N)
# 初始化参数
w1 = np.random.randn(D_in, H)
b1 = np.zeros((H, N))
w2 = np.random.randn(H, D_out)
b2 = np.zeros((D_out, N))
# 学习率
learning_rate = 1e-6
loss_list = []
# 最大跌打次数
iter = 500
for i in range(iter):
    # 前向传播
    h = np.matmul(w1.T, x)+b1 # (100, 64)
    a = np.maximum(h, 0) # (100, 64) relu激活函数
    y_pred = np.matmul(w2.T, a)+b2 # (10, 64)
    # 损失函数
    loss = np.square(y_pred-y).sum()
    loss_list.append(loss)
    # 反向传播
    grad_y_pred = 2*(y_pred-y) # (10, 64)
    grad_w2 = np.matmul(a, grad_y_pred.T) # (100, 10)
    grad_b2 = grad_y_pred # (10, 64)
    grad_a = np.matmul(w2, grad_y_pred) # (100, 64)
    grad_a[a<0] = 0
    grad_w1 = np.matmul(x, grad_a.T) # (1000, 100)
    grad_b1 = grad_a # (100, 64)
    # 更新参数
    w1 -= learning_rate*grad_w1
    b1 -= learning_rate*grad_b1
    w2 -= learning_rate*grad_w2
    b2 -= learning_rate*grad_b2
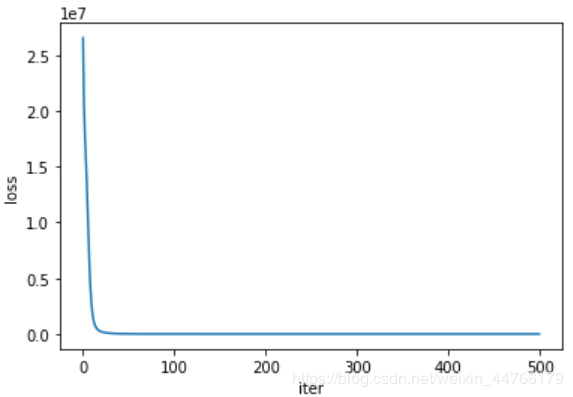
plt.plot(range(iter), loss_list)
plt.ylabel('loss')
plt.xlabel('iter')
plt.show()

在这里插入图片描述