通俗易懂！视觉slam第四部分——slam刚体三维空间运动

日常生活的空间是三维的，因此我们生来就习惯于三维空间的运动。三维空间由三个轴组成，所以一个空间点的位置可以由三个坐标指定。不过，我们现在要考虑刚体，它不光有位置，还有自身的姿态。相机也可以看成三维空间的刚体，于是位置是指相机在空
间中的哪个地方，而姿态则是指相机的朝向。结合起来，我们可以说，“相机正处于空间(0,0,0) 点处，朝向正前方” 这样的话。但是这种自然语言很繁琐，我们更喜欢用数学语言来描述它。

首先是内外积：

对于 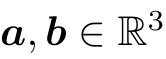，内积可以写成：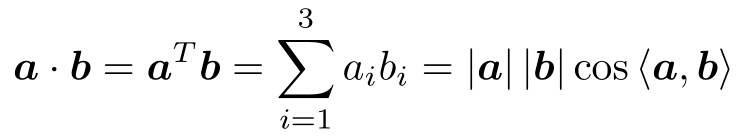

内积可以描述向量间的投影关系。

外积：

外积的方向垂直于这两个向量，大小为 |a||b|sin〈a,b〉，是两个向量张成的四边形的有向面积。对于外积，我们引入了∧符号，把 a 写成一个矩阵。事实上是一个反对称矩阵（Skew-symmetric），你可以将∧记成一个反对称符号。这样就把外积 a × b，写成了矩阵与向量的乘法 a ∧ b，把它变成了线性运算。这个符号将在后文经常用到，请记住它。外积只对三维向量存在定义，我们还能用外积表示向量的旋转。

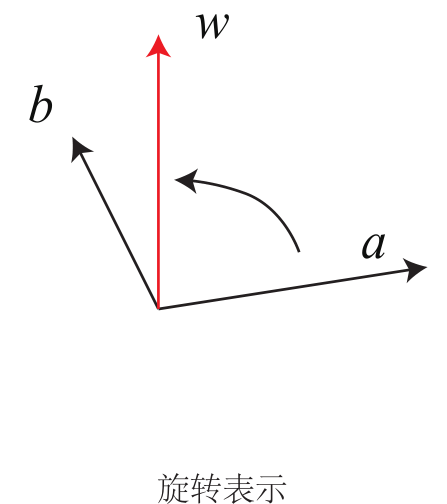
考虑两个不平行的向量 a,b，我们要描述从 a 到 b 之间是如何旋转的，如图所示。我们可以用一个向量来描述三维空间中两个向量的旋转关系。在右手法则下，我们用右手的四个指头从 a 转向 b，其大拇指朝向就是旋转向量的方向，事实上也是 a × b 的方
向。它的大小则由 a 和 b 的夹角决定。通过这种方式，我们构造了从 a 到 b 的一个旋转向量。这个向量同样位于三维空间中，在此坐标系下，可以用三个实数来描述它。

 欧式变换

相机运动是一个刚体运动，它保证了同一个向量在各个坐标系下的长度和夹角都不会发生变化。这种变换称为欧氏变换。想象你把手机抛到空中，在它落地摔碎之前，只可能有空间位置和姿态的不同，而它自己的长度、各个面的角度等性质不会有任何变化。这样一个欧氏变换由一个旋转和一个平移两部分组成。首先来考虑旋转。我们设某个单位正交基(e 1 ,e 2 ,e 3 ) 经过一次旋转，变成了 (e′1 ,e′2 ,e′3 )。那么，对于同一个向量 a（注意该向量并没有随着坐标系的旋转而发生运动），它在两个坐标系下的坐标为 [a 1 ,a 2 ,a 3 ] T 和 [a′1 ,a′2 ,a′3 ] T 。根据坐标的定义，有：

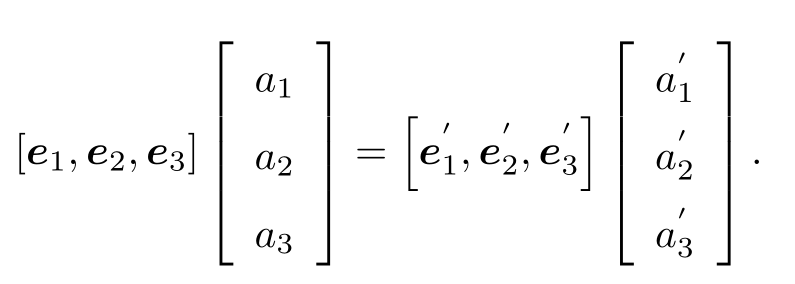
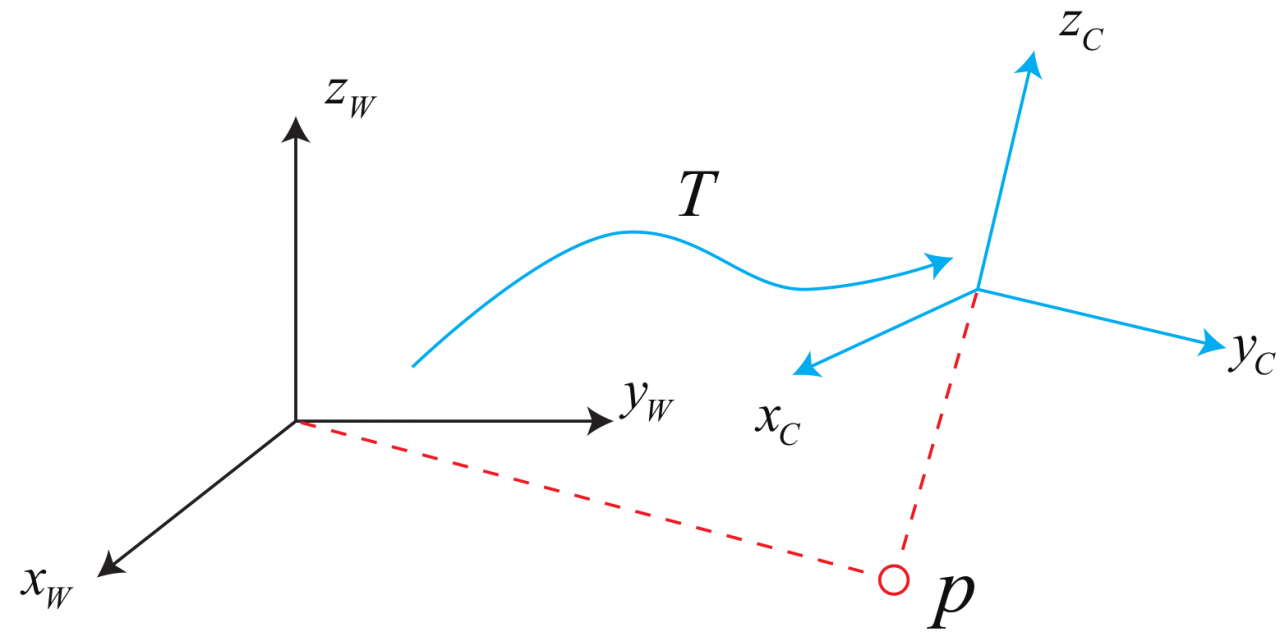
坐标变换。对于同一个向量 p，它在世界坐标系下的坐标 pw 和在相机坐标系下的 pc 是不同的。这个变换关系由坐标系间的变换矩阵 T 来描述。

 为了描述两个坐标之间的关系，我们对上面等式左右同时左乘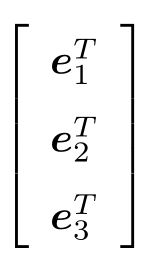那么左边的系数变成了单位矩阵，所以：

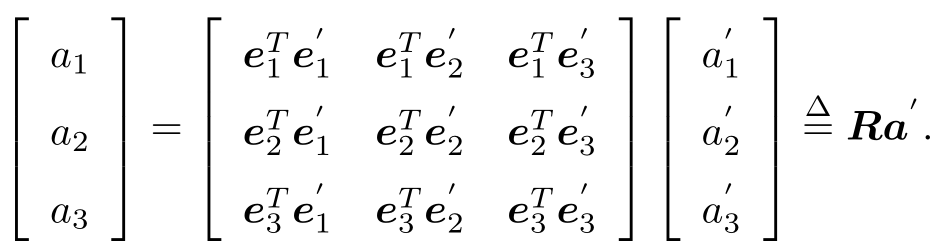
我们把中间的阵拿出来，定义成一个矩阵 R。这个矩阵由两组基之间的内积组成，刻画了旋转前后同一个向量的坐标变换关系。只要旋转是一样的，那么这个矩阵也是一样的。可以说，矩阵 R 描述了旋转本身。因此它又称为旋转矩阵。 

旋转矩阵有一些特别的性质。事实上，它是一个行列式为 1 的正交矩阵 。反之，行列式为 1 的正交矩阵也是一个旋转矩阵。所以，我们可以把旋转矩阵的集合定义如下：

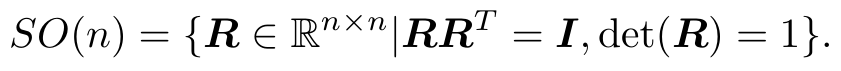
SO(n) 是特殊正交群（Special Orthogonal Group）的意思。我们把解释“群”的内容留到下一讲。这个集合由 n 维空间的旋转矩阵组成，特别的，SO(3) 就是三维空间的旋转了。通过旋转矩阵，我们可以直接谈论两个坐标系之间的旋转变换，而不用再从基开始谈起了。换句话说，旋转矩阵可以描述相机的旋转。由于旋转矩阵为正交阵，它的逆（即转置）描述了一个相反的旋转。按照上面的定义方式，有：

显然  刻画了一个相反的旋转。在欧氏变换中，除了旋转之外还有一个平移。考虑世界坐标系中的向量 a，经过一次
旋转（用 R 描述）和一次平移 t 后，得到了 a′ ，那么把旋转和平移合到一起，有： 

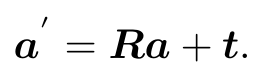
其中，t 称为平移向量。相比于旋转，平移部分只需把这个平移量加到旋转之后的坐标上，显得非常简洁。通过上式，我们用一个旋转矩阵 R 和一个平移向量 t 完整地描述了一个欧氏空间的坐标变换关系。

三维空间 slam 运动