区块链上居然可以用“彩票”支付?
区块链要想真正商业落地,不可避免地要在区块链上做支付结算,那么我们就需要尽可能地降低支付的成本,换言之也就是尽可能地减少上链的操作。
而概率微支付就是针对这一问题的解决方案之一。
概率支付的最初概念早于区块链技术,在1996年,David Wheeler 首次发论文阐述概率支付的概念以及如何将其应用于使用随机数字承诺的电子协议。
接着1997年,Ronald Rivest 发表了论文,提出了如何在电子微支付中应用概率支付。
到2015年,Pass 和 Shelat 在论文「Micropayments for Decentralized Currencies」中提出了如何将概率微支付应用于BTC等通证,并指出先前的方案都依赖于可信的第三方。
近些年概率支付的研究也逐渐扩展到零知识证明,并以此来构建区块链协议的去中心化和匿名微支付。
在了解概率微支付前,我们先来了解下什么是微支付以及为什么需要微支付。
微支付
支付一词,在现实世界中大家再熟悉不过了,到商店买瓶可乐,上网买个手机都需要涉及到支付。但到了区块链世界,这个简单的支付就稍微变得复杂了。因为交易的双方都不信任对方,双方都认为对方有作恶的可能性。
举个具体的例子:
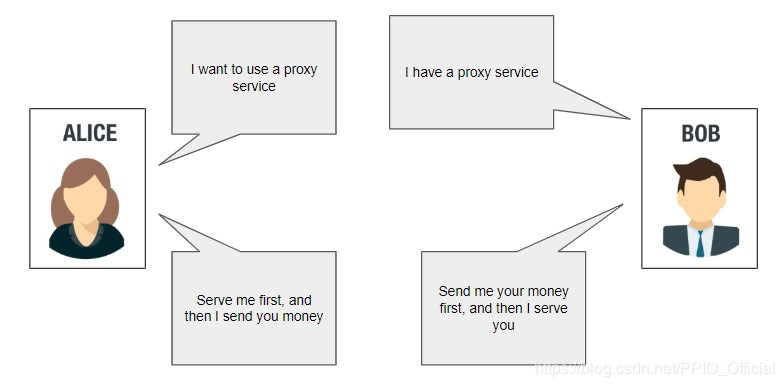
假设 Alice 与 Bob 在以太坊上交易,Alice 用 ETH 购买 Bob 提供的带宽服务。在这个场景下,如果 Alice 先向 Bob 支付,那么她就会担心 Bob 作恶,即 Bob 拿了钱却不为她提供带宽服务。但同时 Bob 也会担心如果他先提供服务,Alice 会作恶,即 AIice 使用带宽服务后拒绝付款。
因此,双方因信任问题无法展开交易。
在现实世界中,这个问题是如何解决的呢?
没错,是依靠可信的第三方。
Alice 先把钱托管给可信第三方,当 Bob 看到 Alice 已经将钱托管后,才开始服务 Alice,服务完成之后可信第三方将托管资金转入 Bob 账户。这过程中任何一方作恶,另一方都可以通过举证,寻求这个可信第三方来仲裁。
但在区块链世界,没有这种可以根据事实证据来仲裁的可信第三方。所以我们退而求其次,通过缩小交易额度来降低风险,即将一个大额交易拆分成一个个的小额交易进行。
例如,Alice 需要 从 Bob 那里下载 100GB 的数据,总共需要向 Bob 支付 1 个 ETH。如果 Alice 先转账 1 个 ETH 给 Bob,然后 Bob 再把数据给 Alice ,那么 Alice 就会担心 1 ETH 转过去之后,Bob 不给她数据。
因此,Alice 可以把这次交易拆成 100 份,即 Alice 先转 0.01 ETH 给 Bob,Bob 收到 0.01 ETH 后传给 Alice 1GB 的数据;Alice 确认收到的数据无误后,再给 Bob 转第二个 0.01 ETH,然后 Bob 再给 Alice 传输第二个 1GB 的数据;依此类推,直到 100GB 都传输完毕,完成交易。
如果Bob在中间某次交易过程中作恶,比如,Bob 收到第 n 个 0.01 ETH 后不再给 Alice 数据了,那么 Alice 最多也只损失 0.01 ETH,不会有太大的损失。同样的道理,如果把交易分成 1千份,1万份,那么因对方作恶而导致己方的损失将会更低。
以上这种将大额支付拆解成小额支付以降低交易风险的支付方式叫做“微”支付。
微支付解决了两个不可信角色之间的交易问题,它没有本质上解决交易的风险,而是将交易的风险降到了较小的范围。
支付通道
“微支付”虽然可以使得互相不信任对方的两个人之间可以进行交易,但在链上具体实现该方案的时候,会遇到一个成本问题。
我们都知道链上转账是付款者发送一个转账交易,当交易被出块节点打包进区块并确认后,才算转账成功。但发送交易是有成本的:
发送交易需要手续费,例如在以太坊上,发送交易需要燃烧 Gas ; 交易的确认需要时间,少则分钟级别,多则小时级别;考虑金钱成本和时间成本,那么链上的微支付就变得不具有可行性。
例如,Alice 每次付 0.01个 ETH Bob,就发送一次转账交易,交易烧掉的 Gas 费可能就要 0.005 个 ETH,而且双方为了转账确认到账,必须等待几十分钟后才可进行第二次小额交易。
很明显这样手续费太高了,效率太低了。
因此,减少发送上链交易的次数,并且缩短转账等待的时间成为必须克服的问题。
正好支付通道可以解决这两个问题。支付通道也被称为状态通道,严格意义上讲支付通道是状态通道的子集。支付通道的本质是一个可以托管资金的智能合约,但从该合约提款必须满足特定的条件。
支付通道按照支付方向可分为单向的支付通道和双向的支付通道。
以单向支付通道为例,Alice 可以预先把足够的消费款托管在支付通道合约中,并在合约中指定收款方只能是 Bob。然后每次支付过程中,Alice 链下给 Bob 一个凭据。凭据中包含了通道的地址、支付的金额,Nonce 值,以及 Alice 签名。Bob 收到该凭据后,就可以凭借该凭据到支付通道合约中提款。但 Bob 不需要一收到凭据就立刻提款,他完全可以等到交易结束后凭借最后一个凭据一次性提走整个交易的款。
能达到这样效果的原因是,凭据是一种增量支付凭据。即,Alice 第一次给 Bob 的支付凭据中的金额是 0.01 ETH,第二次给Bob的支付凭据是 0.02 ETH,……以此类推。因此 Bob 只要收到的新的更大额的凭据,老的小额凭据就没有用了,他只需要保留最新的且有效的凭据,在交易结束后,Bob 用该凭据提款即可。
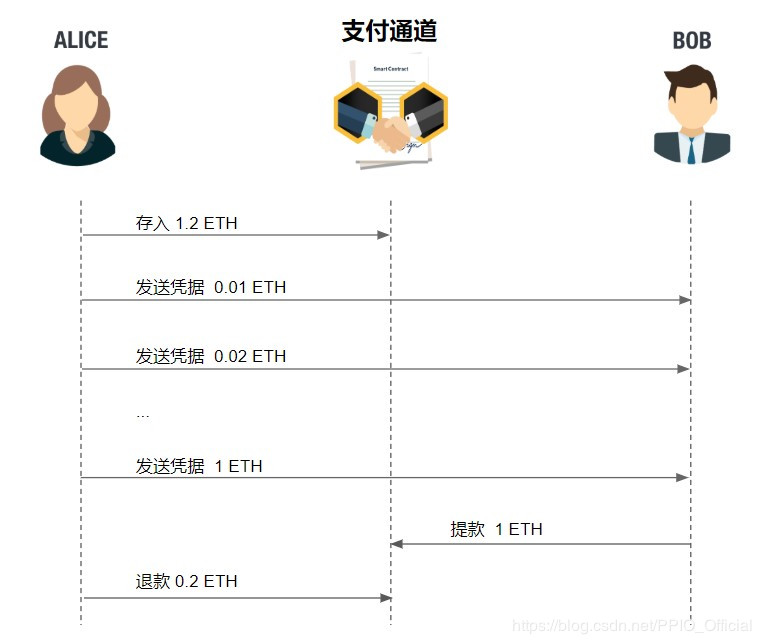
所以,基于支付通道,没有人作恶的情况下,一般两次上链操作就可以完成双方的交易。这大大提高了交易的效率,降低了交易的成本。
概率微支付
虽然上面说的一对一的支付方案已经可以落地了,但是现实的互联网场景很多时候都是需要一对多支付的。
例如下载场景,通常是一个用户向多个下载服务器请求下载同一个资源,这样可以更快地下载完成,那么这个用户就需要跟多个下载服务提供者建立支付通道。并且每个下载服务提供者在下载完成后都要上链提一次款。这会对链造成很大的压力。
这时候概率微支付就发挥它的神奇作用了。
概率微支付,是在微支付的基础上加上概率性,简单的说,收款者会以一定的概率收到款,并且他收到款的数学期望与他应当收到的款相同。
举例说明:
Alice 同时与两个服务提供者交易,如果按照标准的单向支付通道的做法, Alice 需要上两次链,将预付款分别托管到两个支付通道中,然后每次发送 0.01ETH 的凭据给服务提供者,并且最后每个服务提供者都需要上链提一次款。
如果改用概率微支付的方案。Alice 只需要一次性的将预付款打入一个合约,然后以 1%的概率向服务提供者支付 1 ETH。如果 Alice 所使用的总服务量不变,那么最终在概率上来看,只有一个服务提供者会收到 1 ETH的凭据。
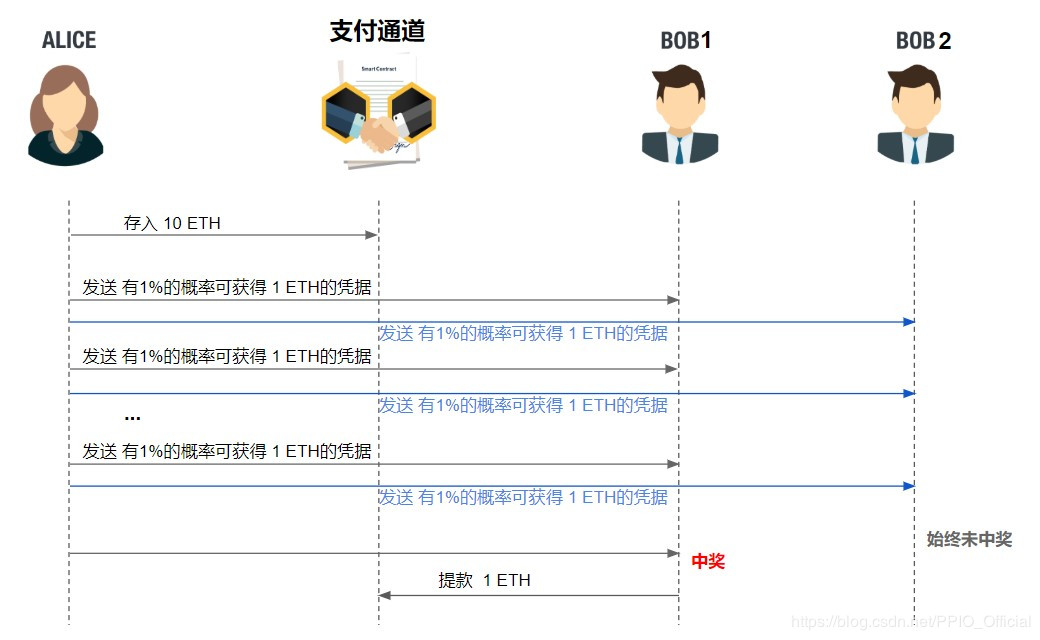
当然,既然是概率性的,也会碰到特殊情况,即 Alice 在使用服务过程中有 n 个凭据中奖,这样Alice就实际付了 n 个 ETH。n 可能大于 1(付了多于 1 ETH 的钱),也可能等于 0(没付钱,免费享受服务)。不过从长期来看,上述例子中,Alice平均每次所付的款会逼近数学期望即 1 ETH * 1% 即 0.01 ETH。
换句话说,只要 Alice 长期使用概率支付,那么她不会吃亏也不会赚到便宜。
概率微支付的原理
那么这种神奇的概率支付背后的原理是什么呢?
答案是随机性。
Alice 在概率性支付给 Bob 之前,Bob 首先要随机生成一个随机数 secret ,然后 Bob 将 secret 的摘要,即 Hash(secret) ,发送给 Alice 。
然后 Alice 将(ChannelAddress,Hash(secret),BobAddress,Nonce,FaceValue,WinProp)以及对这些数据的签名SigAlice 作为凭据发送给 Bob。
其中,ChannelAddress 是支付通道的地址;BobAddress 是 Bob 的钱包地址;Nonce 在通道中的 Nonce 值,用于防重放;FaceValue 是面额值,例如 1 ETH;WinProp 是中奖比率乘以 2^256 的值,例如 1% 的中奖概率对应的 WinProp = 0.01 * (2^256)。
Bob 收到凭据后,自己就可以判断是否中奖了,方法如下:
Bob 计算 h1 = Hash(ChannelAddress,Hash(secret),BobAddress,Nonce,FaceValue,WinProp,SigAlice), h2 = Hash(h1, secret),如果 h2 < WinProp 则中奖,Bob 就可以用这个凭据到通道中取款了。
由于Alice在为凭据签名的那一刻不知道 Bob 的 secret,因此 Alice 无法构造签名使得 Bob 不中奖。同时 Bob 在随机生成 secret 的那一刻,他也没有 Alice 对凭据的签名,因此也无法构造一个必然中奖的 secret。
由此可见,双方都无法作弊。支付成功的唯一因素就是概率。
总结
概率微支付是一种很有意思的支付思想,它通过概率性,相当于将多次微支付聚合了。这种聚合可以使得更少的上链。
传统的支付方案中的支付具有确定性。付款者在每次支付操作中都会向收款者支付一定费用的提款凭据,收款者利用该提款凭据,一定可以在链上通道合约中提到款,简单地说就是,付款者付了钱,收款者就一定能收到钱。
而概率微支付方案中,付款者在每次支付操作中不会向收款者支付确定性的提款凭据,取而代之的是一种不确定性的提款凭据,这种新的凭据有点类似「彩票」。收款者接收到这种「彩票」后,自己可以开奖,如果中奖,那么该「彩票」就变成了确定性的提款凭据,可以在链上通道合约中提到款;如果没有中奖,则该「彩票」就变成了废票,一文不值。至于中奖的因素完全取决于随机,付款方和收款方都不能单方面左右。
但概率微支付的不确定性有其优点也有其缺点:
某些时候会导致付款方付出比实际应付的款要多的资金,相当于多付了;某些时 候又会导致服务方一直不中奖而得不到报酬; 虽然概率微支付在一对多支付场景下有其优势,但是一对多的支付本质上也增加了双花的风险性,因此支付者必须在合约中抵押足够多的资金才能降低这种风险,使得服务方愿意与其交易。因此,是否采用概率微支付,需要根据实际场景综合考虑来决定。不过从概率微支付中我们学到的不仅仅是一个技术方案,更重要的是它的思想。它启发我们,确定性和效率可以在一定范围内相互转换。

作者:PPIO