基于奇异值分解(SVD)的图片压缩实践
数字图片在计算机中是以矩阵形式存储的。所以可以通过矩阵理论和矩阵算法对数字图像进行分析和处理。本文通过对图片进行SVD压缩,对不同的参数下的压缩效果进行对比。
SVD概念可以参考:《统计学习方法》–奇异值分解(Singular Value Decomposition,SVD)
2. 原理简介彩色图片有3个图层,RGB(红、绿、蓝)也就是矩阵的一个位置上存储了3个基色的数值,由3个基色混合成不同的色彩。
通过对3个图层矩阵,分别进行SVD近似,SVD奇异值是唯一的,可以取前 k 个最大的奇异值进行近似表达,最后再将3个图层的矩阵数据合并,用较少的数据去表达图片。
2.1 SVD定义Am×n=UΣVTUUT=ImVVT=InΣ=diag(σ1,σ2,...,σp)σ1≥σ2≥...≥σp≥0p=min(m,n)A_{m \times n} = U \Sigma V^T\\ UU^T=I_m\\ VV^T=I_n\\ \Sigma=diag(\sigma_1,\sigma_2,...,\sigma_p) \\ \sigma_1\ge \sigma_2 \ge...\ge\sigma_p \ge0\\ p=\min(m,n)Am×n=UΣVTUUT=ImVVT=InΣ=diag(σ1,σ2,...,σp)σ1≥σ2≥...≥σp≥0p=min(m,n)
UΣVTU \Sigma V^TUΣVT 称为矩阵 AAA 的奇异值分解(SVD),UUU 是 mmm 阶正交矩阵, VVV 是 nnn 阶正交矩阵,Σ\SigmaΣ 是 m×nm \times nm×n 的对角矩阵 σi\sigma_iσi 称为矩阵 AAA 的奇异值 UUU 的列向量,左奇异向量 VVV 的列向量,右奇异向量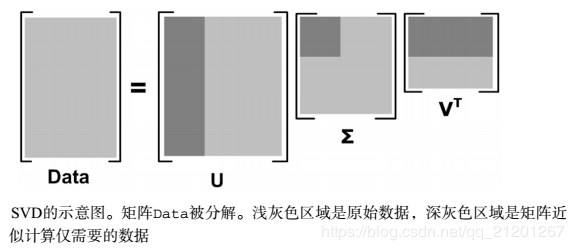
Datam×n≈U[:,0:k]Σ[0:k,0:k]VT[0:k,:]Data_{m\times n} \approx U[ : , 0:k] \Sigma[0:k,0:k]V^T[0:k, :]Datam×n≈U[:,0:k]Σ[0:k,0:k]VT[0:k,:]
# -*- coding:utf-8 -*-
# @Python Version: 3.7
# @Time: 2020/4/21 23:38
# @Author: Michael Ming
# @Website: https://michael.blog.csdn.net/
# @File: 15.svd_pic_compress.py
# @Reference: https://blog.csdn.net/weixin_44344462/article/details/89401727
import numpy as np
import matplotlib.pyplot as plt
def zip_img_by_svd(img, plotId, rate=0.8):
zip_img = np.zeros(img.shape)
u_shape = 0
sigma_shape = 0
vT_shape = 0
for chanel in range(3): # 3个图层
u, sigma, v = np.linalg.svd(img[:, :, chanel]) # numpy svd函数
sigma_i = 0
temp = 0
while (temp / np.sum(sigma)) < rate: # 选取的奇异值和需要达到设定的权重
temp += sigma[sigma_i]
sigma_i += 1
SigmaMat = np.zeros((sigma_i, sigma_i)) # 选取了sigma_i 最大的奇异值
for i in range(sigma_i):
SigmaMat[i, i] = sigma[i] # 将奇异值填充到Sigma对角矩阵
zip_img[:, :, chanel] = u[:, 0:sigma_i].dot(SigmaMat).dot(v[0:sigma_i, :])
# 将分解得到的3个矩阵相乘,得到压缩后的近似矩阵
u_shape = u[:, 0:sigma_i].shape
sigma_shape = SigmaMat.shape
vT_shape = v[0:sigma_i, :].shape
for i in range(3): # 对三个通道的矩阵数值进行归一化处理
MAX = np.max(zip_img[:, :, i])
MIN = np.min(zip_img[:, :, i])
zip_img[:, :, i] = (zip_img[:, :, i] - MIN) / (MAX - MIN)
zip_img = np.round(zip_img * 255).astype("uint8")
# 不乘255图片是黑的(接近0,0,0),数据类型uint8
plt.imsave("zip_svd_img.jpg", zip_img) # 保存压缩后的图片
zip_rate = (img.size - 3 * (
u_shape[0] * u_shape[1] + sigma_shape[0] * sigma_shape[1] + vT_shape[0] * vT_shape[1])) / (zip_img.size)
f = plt.subplot(3, 3, plotId)
f.imshow(zip_img)
f.set_title("SVD压缩率 %.4f,奇异值数量:%d" % (zip_rate, sigma_i))
print("设置的压缩率:", rate)
print("使用的奇异值数量:", sigma_i)
print("原始图片大小:", img.shape)
print("压缩后用到的矩阵大小:3x({}+{}+{})".format(u_shape, sigma_shape, vT_shape))
print("压缩率为:", zip_rate)
if __name__ == '__main__':
imgfile = "svd_img.jpg"
plt.figure(figsize=(12, 12))
plt.rcParams['font.sans-serif'] = 'SimHei' # 消除中文乱码
img = plt.imread(imgfile)
f1 = plt.subplot(331) # 绘制子图,3行3列,3*3个子图,现在画第1幅
f1.imshow(img)
f1.set_title("原始图片")
for i in range(8): # 再画8个子图
rate = (i + 1) / 10.0 # 压缩率 10% - 80%
zip_img_by_svd(img, i + 2, rate)
plt.suptitle('图片SVD效果对比', fontsize=17, y=0.02) # y偏移距离
plt.show()

703x800的尺寸,SVD使用的矩阵 ((703, 128)+(128, 128)+(128, 800))=208768
可以少使用的矩阵数据比例为(703*800*3-208768*3)/(703*800*3)= 62.88%
可以只用37.12%的数据量去近似表达原始图片,是不是很酷!!!
在网络传输图片的过程中,终端用户可能点击,也可能不点击,那我都给他们发送SVD后的图片矩阵数据(减少了当次传输数据量),然后在终端进行矩阵运算得到压缩后的图片,当用户点击图片后,再进行传输原图片(1、用户点击是分散的,可以降低统一发送原图的网络拥挤现象;2、有的用户也不会点击,就避免了传输原图,达到了压缩的目的,节省流量)
微信收到的图片、小米手机云相册的缩略图等都可能用到类似的技术来节省空间
我是外行,自己想的结论,不对的地方,请大佬指点,感谢!
本文参考了以下两篇文章,对作者表示感谢!
利用SVD进行图像压缩(附Python代码) 用SVD压缩图像作者:Michael阿明