关于拉氏变换和频谱图的那些事儿

Beatrice ·

更新时间:2024-11-11

· 930 次阅读

目录摘要拉氏变换简介傅里叶变换vs拉氏变换拉氏变换表示例以及结果方法1定义法频谱图定义结果图完整代码方法2bode图摘要

最近小虎在网课上被老师问到编程写出一指数函数y=Ae−aty=Ae^{-at}y=Ae−at的频谱图，当时鼓捣了1个多钟？？？以前是画过bode图，bode的幅频图是对数幅频图。应该也可以用博得图直接画的，但是这个问题的关键应该在拉氏变化。5分钟不到的事，要搞那么久，看来是小虎还不太理解拉氏变换。编程工具还是那熟悉的MATLAB。

拉氏变换简介

拉普拉斯变换(Lapalace transform)，是一种线性变换，也就是说非线性不可以用这种方法。一般来讲，满足同质性f(ka)=kf(a)和可加性f(a+b)=f(a)+f(b)，即为线性变换，参考这里。它可以将时域变量转换为复数变量进而得到复数频率。

傅里叶变换vs拉氏变换

既然都是将时域信息转化为频域信息，那么拉氏变换和傅里叶变换(fourier transform)有啥区别呢？
wikipedia说，“The Laplace transform is similar to the Fourier transform. While the Fourier transform of a function is a complex function of a real variable (frequency), the Laplace transform of a function is a complex function of a complex variable.”他们主要区别是变量形式不同，在傅里叶变换是关于实数频率变量的方程，而拉氏变换是关于复数频率变量的方程。
不过两种时域to频域的变换工程上都有应用，像小虎用过的，数字图像处理滤波用过傅里叶变换、傅里叶反变换；自动控制用过拉氏变换求传递函数以及系统的动态特性等等。
傅里叶变换
X(ω)=∫−∞∞x(t)e−jωtdtX(\omega)=\int ^\infty_{-\infty} x(t)e^{-j\omega t}dtX(ω)=∫−∞∞x(t)e−jωtdt
拉氏变换
F(s)=L[f(t)]=∫0∞e−stf(t)dtF(s)=L [f(t)]=\int ^\infty_0 e^{-st}f(t)dtF(s)=L[f(t)]=∫0∞e−stf(t)dt

拉氏变换表

看下面其中一个网站：
Laplace Transform
Microsoft Word - New Laplace Transform Table

示例以及结果

待求频谱函数是指数函数y(t)=Ae−aty(t)=Ae^{-at}y(t)=Ae−at。
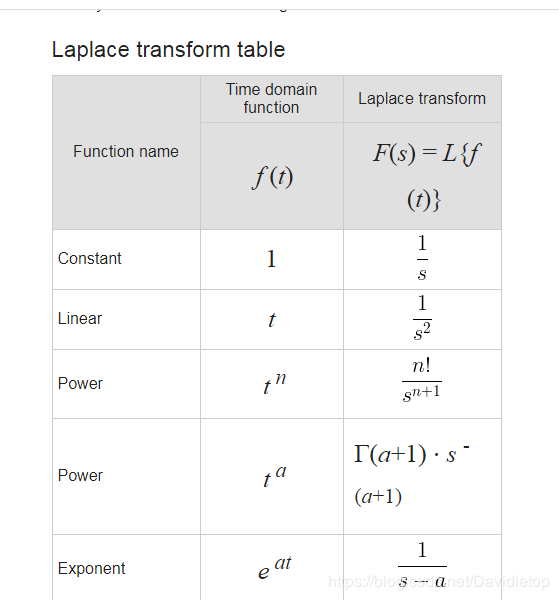
首先查拉氏变换表，的到exponent function的拉氏变换，上述函数的转换结果是：
Y(s)=As+aY(s)=\frac {A}{s+a}Y(s)=s+aA
设A=5，a=5。接下来提供提供两种方法画频谱图，两种方法表示不同，应用场景有点区别。
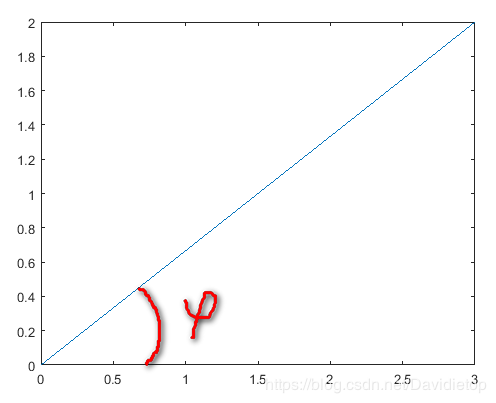
在这里插入图片描述

方法1定义法 频谱图定义

幅值关于频率变化的函数绘制出来的图像称为幅频图，函数可以表示为∣X(ω)∣|X(\omega)|∣X(ω)∣；相位角关于频率变化的函数绘制出来的图像称为相频图，函数可以表示为φ(ω)\varphi(\omega)φ(ω)。幅度可以对函数取绝对值得到，而相位角，可以从复平面得到，比如
z=3+j2z=3+j2z=3+j2
它的幅值为32+22=13\sqrt {3^2+2^2}=\sqrt {13}32+22=13，相位角为：φ=arctan32\varphi=arctan \frac 32φ=arctan23
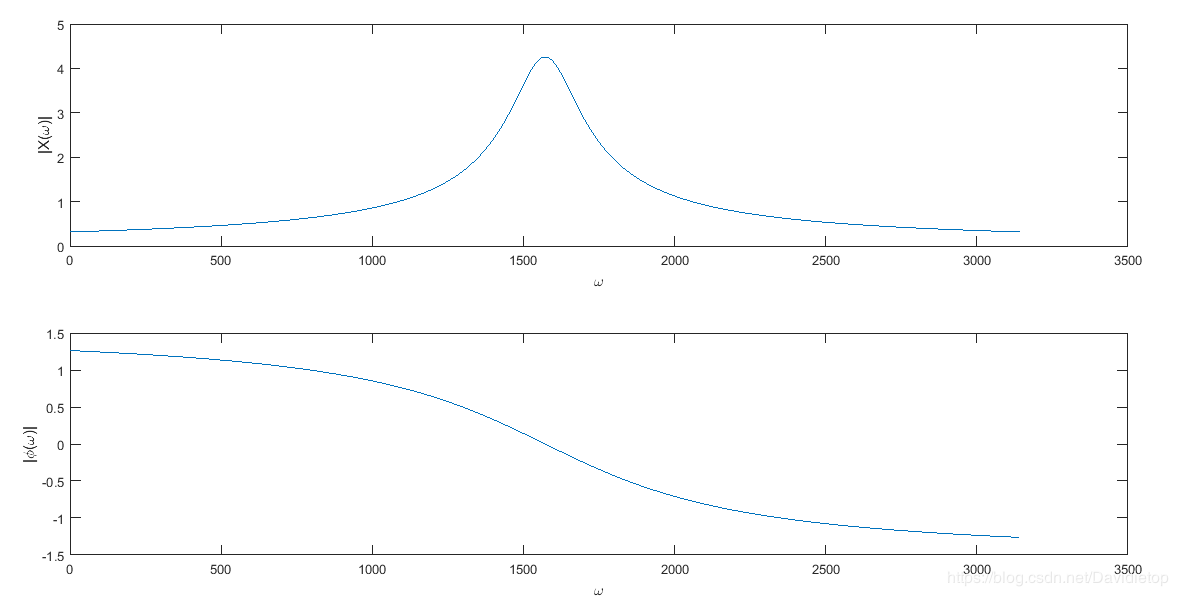
在这里插入图片描述

结果图

在这里插入图片描述

完整代码

a=5;A=5;
w=-5*pi:0.01:5*pi;
Xw=A./sqrt((w.^2+a^.2));
phi=-atan(w/a);
subplot(2,1,1);
plot(Xw);
xlabel('\omega');
ylabel('|X(\omega)|');
subplot(2,1,2);
plot(phi);
xlabel('\omega');
ylabel('|\phi(\omega)|');

此法用于一般情况下求频谱图。

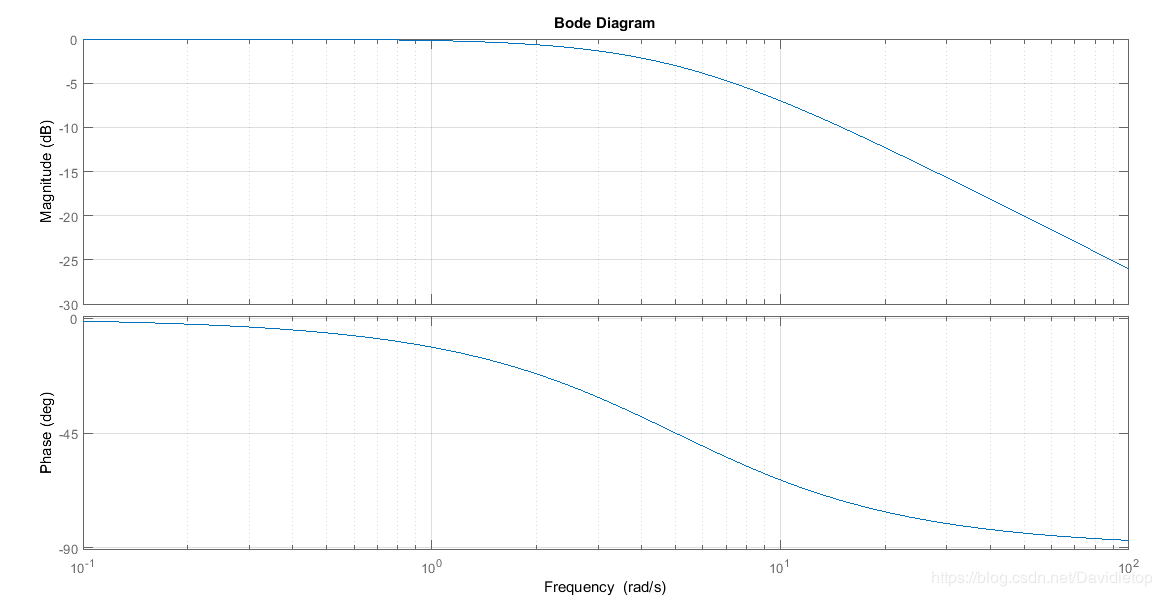
方法2bode图

bode图的意义和编程方法见小虎的这篇文章，这里不再赘述。结果图如下。
在这里插入图片描述