《OpenGL超级宝典》第一章:3D图形和OpenGL简介
摘要:最早的计算机是由一行行的开关和灯组成的(ENIAC)。 技术人员和工程师需要工作几个小时、几天甚至几星期,对这些机器进行编程,并阅读他们的计算结果。随着时间的变迁,这一切逐渐发生了变化。数据可以有效地存储在磁带、磁盘上,甚至可以一行行地存储在打孔纸上,或者存储在一堆穿孔卡上(穿孔纸带)。
1.1.1 进入电子时代摘要:
①. 纸作为计算机的输出媒体非常实用,直到今天仍然是主要的输出媒体之一。但为常规的显示媒体,纸可能显得过于昂贵了。一直用纸作为输出媒体会浪费自然资源,尤其在绝大多数情况下,我们实际上并不需要对计算结果或数据库查询进行硬复制的输出。
②. 作为计算机的一种辅助设备,阴级射线管(CRT)是一项震撼人心的技术。作为最初的计算机监视器(显示器),一开始只是一种显示ASCII文本的视频终端(类似CMD黑窗口)。但是,CRT能够完美地绘制点和线,以及字母字符。不久,其他符号和图形陆续补充到字符终端。程序员使用计算机和监视器创建图形,作为文本或表格输出的补充。随后,一些用于绘制执行和曲线的算法被开发出来,并公布于众。于是,计算机图形逐渐从一项业余爱好变成了一门科学。
③. 最初,显示在这些终端上的计算机图形是二维的,或简称为2D。人们开始用平面的直线、圆和多边形来进行创建组合各种各样的图形。那些富有探索精神的程序员甚至创建了一些简单的街机游戏(如 Lunar Lander、Pong)。他们所使用的简单图形就是由各种线型所绘制的,并且每秒刷新数次(重绘)。
1.1.2 走向3D三维(或3D)这个术语表示一个正在描述或显示的物体具有3个维度:宽度、高度和深度。
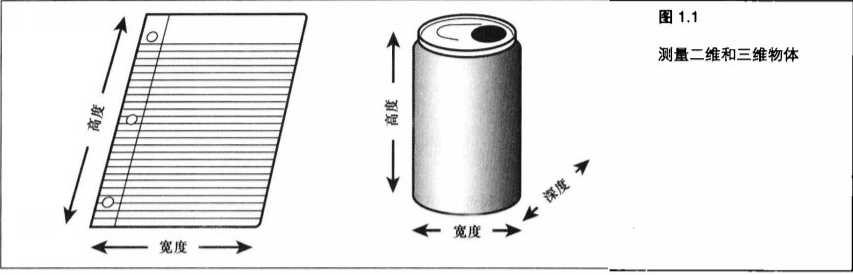
例如,放在书桌上的一张纸(上面画了一些图形或写了一些字)是个二位物体,因为它没有可以令人感觉得到的深度。
但是,放在它旁边的一罐苏打水却是个三维物体。这个苏打饮料罐又大又圆(宽度和高度)又长(深度)。
类似的,计算机3D图形在实质上也是平面的,它只是在计算机屏幕上所显示的二位图像,但它可以提供深度(或第3维)的错觉。(2D + 透视 = 3D)
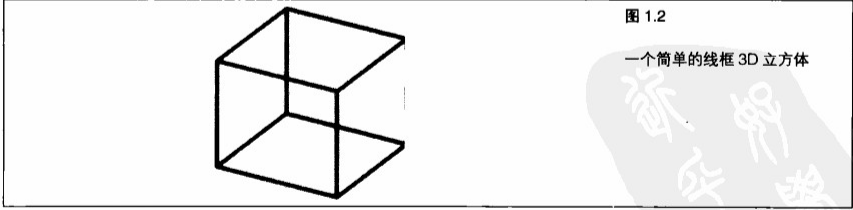
最初的计算机图形看上去类似(图1.2)所示图形,通过12条线段组成了一个简单的三维立方体。使这个正方体看上去具有三维效果的是透视(Perspective),或线段之间的角度。正是它们产生了深度的幻觉。
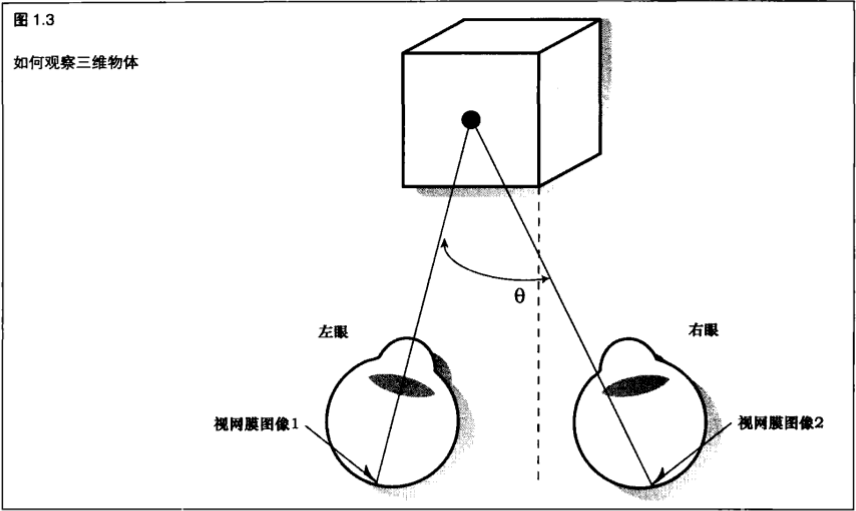
为了真正看到3D图像,实际上需要用两个眼睛观察一个物体,或者为每个眼睛分别提供这个物体的一幅独立而又唯一的图像。(图1.3)
每个眼睛看到的都是一幅二维图像,非常类似于在每个视网膜(位于眼睛的后半部分)上显示了一幅临时照片。随后,大脑对这两幅略微不同的图像进行组合,在脑海中形成一幅单一的、合成的3D图片。
由于计算机屏幕是在平面上显示平面画像,而不是通过不同的视角在两只眼睛上显示两幅图像。这样一来,绝大多数3D计算机图像实际上只是近似3D。
单凭透视本身就足以创建三维的外观。注意前面(图1.2)所显示的那个立方体。即时不着色,这个立方体仍然具有三维物体的外观。但是长时间凝视这个立方体,就会发觉这个立方体的前后将会交换位置。由于图中缺少任何表面着色,大脑将会因此而产生混淆的感觉。这幅图不能提供足够的信息以帮助大脑确定它到底感知到什么。我们遮住一只眼睛时所看到的世界没有突然看起来像平的,原因在于以二维形式观察时,很多3D世界的效果仍然存在。这些效果足以激发大脑判别深度的能力。其中一个线索是由光线照射产生的表面着色,而另一个线索则是近处的物体看起来比远处的物体要大(透视效果)。这种透视效果称为透视缩短(Foreshortening)。这种效果加上颜色的改变、纹理、光照、着色以及各种不同的颜色强度共同组成了我们对三维图像的感知。
本书的每一章都包含一个或多个示例程序用来演示这一章所讨论的编程技术。尽管本章有意避免了关于编程细节的讨论,但仍提供了一个示例程序向读者演示最低程序上所需要熟悉的技术和术语,以帮助读者充分地利用本书。本章的示例程序叫做BLOCK,读者可以从随书提供的示例程序集中的 "Chapter 1"文件夹中找到它。(此示例已上传Github,具体链接会在文末贴出)
将数学和图形数据转换成3D空间图像的操作叫做渲染(Rendering)。当这个术语作为动词使用时,指的是计算机创建三维图像时所经历的过程。它也作为名词使用,指的仅仅是最终的图像作品。这个术语在本书中经常出现。现在我们来看一看渲染过程中出现的其他一些术语和操作。
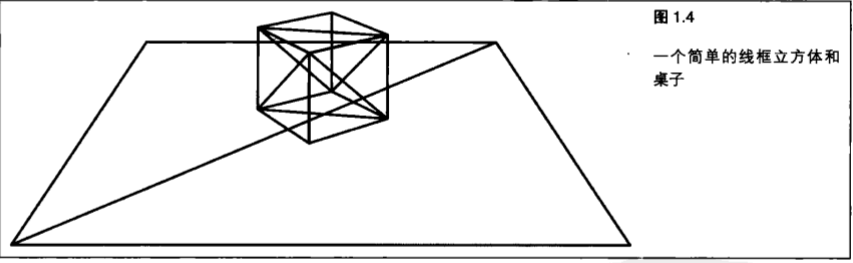
1.2.1 变换(Transformation)和投影(Projection)(图1.4)所示是BLOCK示例程序的原始输出结果,显示的是用线条绘制的一个放置在一张桌子或一个平面上的立方体。通过变换(Transformation),或者说旋转这些点,并在它们之间绘制线段,我们就能在平面的2D屏幕上创造出一个3D世界的错觉。
这些点本身叫做顶点(Vertices,单数为Vertex)(术语:顶点),它们能够通过一种称为变换矩阵(Transformation Matrix)的数学结果进行旋转(本书第4章将详细讲解变换矩阵相关内容)。另外还有一种矩阵叫做投影矩阵(Projection Matrix),用于将3D坐标转换成二维屏幕坐标,实际的线条也将在二维屏幕坐标上进行绘制。
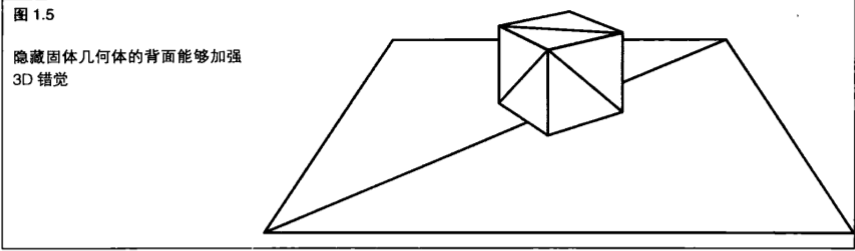
实际绘制或填充每个顶点之间的像素形成线段就叫做光栅化(Rasterization)。我们可以通过隐藏表面消除(Hide Surface Removal)来进一步澄清3D设计意图。(图1.5)所示显示了再BLOCK示例程序第一次按空格键后的输出。虽然使用的仍然是点和线段,但是一个放置在桌面上的正方体的错觉却更加逼真了(相比图1.4)。
虽然用线段绘图【也称做线框渲染(Wireframe Rendering)】也有它的用处,但在大多数情况下我们并不是用线段,而是用实心三角形进行渲染。像线段一样,三角形和多边形也会被光栅化或填充。早期的图形硬件能够用纯色对三角形进行填充,但正如(图1.6)所示的,这样做并不能增强3D错觉。早期的游戏和模拟技术可能会在相邻的多边形上采用不同的纯色,这确实有所帮助,但却不能令人信服地对现实进行模拟。
貌似说了这么多还是没入到正题,光栅化到底是什么呢?(不懂的读者可以去看下这篇博文)
由于(图1.6)看的十分模糊在放一张运行了BLOCK示例的截图

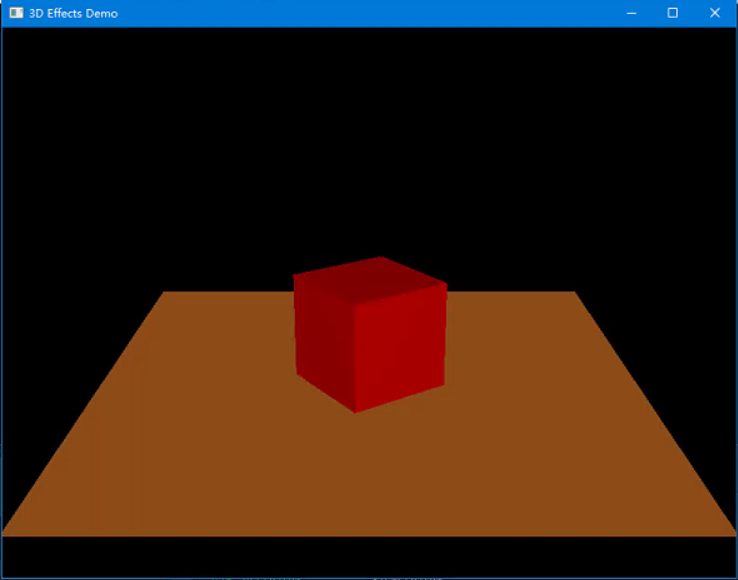
(图1.7)在运行BLOCK按下两次空格键后,将会展示着色(Shading)的效果。通过沿着表面(在顶点之间)改变颜色值,能够轻松创建光线照射在一个红色正方体上的效果。
光照和着色在3D图形专业领域占据了非常大的比重,并且有专门论述它们的书籍。另一方面,着色器(Shader)则是在图形硬件上执行的单独程序,用来处理顶点和执行光栅化任务。

同样的由于(图1.7)看的效果太清楚在放一张运行了BLOCK示例的截图
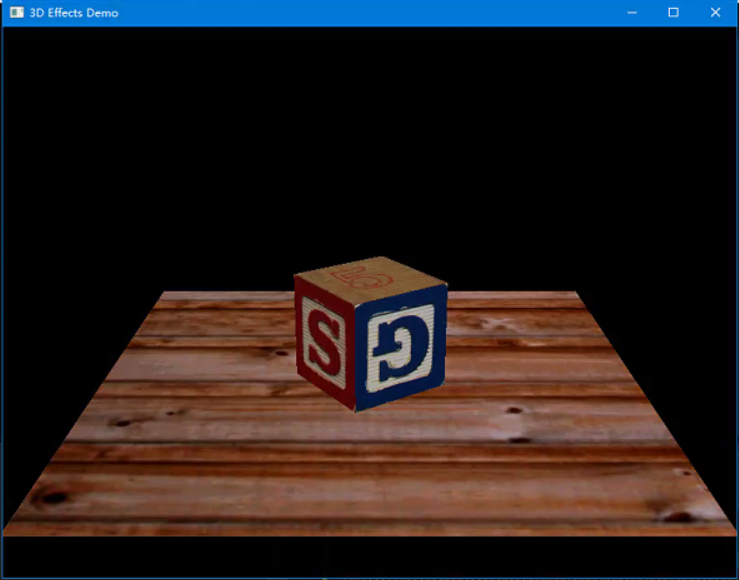
接下来要介绍的硬件技术进步是纹理贴图(Texture Mapping)。一个纹理不过是一幅用来贴到三角形或多边形上的图片。正如我们在(图1.8)中看到的这些纹理将渲染提高到了一个崭新的层次。
在如今的硬件上,纹理是快捷有效的,而一个纹理所能再现的表面如果用三角形来实现的话,可能需要几千甚至几百万个。
这个示例可以通过运行BLOCK后按三次空格进行切换显示。

同样的由于(图1.8)看的效果太清楚在放一张运行了BLOCK示例的截图
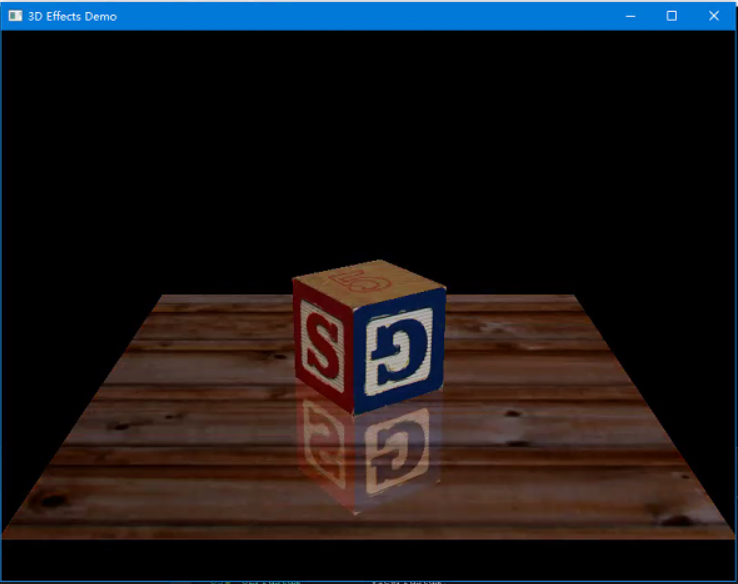
最后,(图1.9)展示了混合(Blending)的效果。混合时我们能够将不同的颜色混合在一起。我们首先上下颠倒地绘制这个立方体,然后再在他的上面绘制地板并与他们进行混合,在绘制正常方向的立方体,就能获得这种反射效果。我们的确"透过"地板看到下面颠倒的立方体。大脑告诉我们,"哦……这是个倒影"。我们也可以应用混合使物体看起来透明。实际上,(图1.9)中真正看到的倒立立方体其实是"透过"地板看到的。
简单说下上面的绘制步骤:
① 绘制倒立立方体
② 绘制地板(应用了混合)
③ 绘制正常方向的立方体

同样的由于(图1.9)看的效果太清楚在放一张运行了BLOCK示例的截图
总而言之,言而总之,总之而言。上述内容大概就是所谓的计算机图形了。实心3D几何体无非就是将顶点间的点连接起来,然后对三角形进行光栅化而使对象变得有实体。变换、着色、纹理与混合---我们在电影、电视、游戏、医疗或商业应用中看到的任何计算机渲染场景都无非是灵活地运用这4中技术产生。
1.3 3D图形的常见用途在现代计算机应用程序中,三维图形具有广泛的应用。实时3D图形的应用范围包括交互游戏和模拟以及数据的可视化显示(供科学、医学或商业应用)。高端3D图形在电影以及技术和教育出版物中也具有广泛的应用。
1.3.1 实时3D如前面所述,实时3D图形是指活动的并与用户进行交互的图形。(实时更新的3D图形)
实时3D图形最早的用途之一是军事飞行模拟器。即使到了今天,飞行模拟器仍然为许多业余爱好者所热衷。
(图1.10)显示了一个流行的飞行模拟器的屏幕截图,它使用了OpenGL进行3D渲染(有兴趣可以去www.x-plane.com体验)。
 1.3.2 非实时3D
1.3.2 非实时3D
在实时3D应用中,我们常常需要作出一些妥协。只要有足够的处理时间,我们就可以创建更高质量的3D图形。
在一般情况下,我们设计模型和场景,并用到一个光线追踪器或扫描线渲染器来处理这些定义,产生高质量的3D图形。
典型的处理过程如下:
① 一个建模应用程序,使用实时3D图形与艺术家(使用者)进行交互,创建具体的内容;
② 然后它所创建的帧被发送到另一个应用程序(光线追踪离线渲染器)或子程序,由他们对图像进行渲染,渲染可能要耗费很长时间。
例如:在一台非常快速的计算机上,为一部电影(例如:熊出没)渲染一个单独的帧可能需要耗费几个小时。渲染并保存成千上万个帧的过程生成了一个可以回放的动画序列。尽管这个动画序列在回放时看上去像实时,但它的内容却不是交互性的。因此,它并不是实时的,而是预渲染的。
1.3.3 着色器在实时计算机图形中,最前沿的艺术是可编程着色器(Programmable Shading)。
今天的图形卡不再是低能的渲染芯片了,而是功能强大的高度可编程的渲染计算机。
每年,基于着色器的图形硬件不断侵占系统上由高端光线追踪器和前面所提到的软件渲染工具所完成的任务。
(图1.16)展示了Software Bisque 的 Seeker 太阳系模拟器上的一幅地球图像。
这个应用程序使用了一个自定义的OpenGL着色器,以每秒60幅的速率生成了一幅逼真的地球动态图像。
它还包括了大气效果、太阳在水中的倒影,甚至背景中的星星。

现在,我们对实时3D的基本概念已经有了相当程度的认识。我们讨论了一些术语以及PC上的一些示例应用程序。那么,如何在自己的计算机上创建这样的图像呢?好吧,这正是本书剩余部分的任务所在。不过,读者还需要知道一些基础知识,这正是我们接下来将要讨论的。
1.4.1 并非工具包OpengGL基本上是一种底层渲染API(应用程序接口 Application Programming Interface)。
我们不能告诉它 "在什么地方绘制什么" -----我们需要自己动手,通过载入三角形,应用必要的变换和正确的纹理、着色器并在必要时应用混合模式来组合一个模型。
这使得我们能够进行大量的底层控制。与使用高层工具包(游戏引擎)相比,使用OpenGL这样的底层API的动人之处在于,我们不能仅仅是重现许许多多的标准3D渲染算法,我们可以创造自己的算法,甚至可以发现一些新的捷径、性能技巧和艺术视觉技术。
1.4.2 坐标系统现在,让我们考虑如何在三维中对物体进行描述。
在指定一个物体的位置和大小之前,需要一个参考帧对它进行测量和定位。
当我们在一个简单的平面计算机屏幕上绘制点和线时,我们根据行和列指定一个位置。(例如: x, y)
在OpenGL或几乎所有的3D API中创建一个用于绘图的窗口时,必须指定希望使用的坐标系统以及指定的坐标如何映射到实际的屏幕像素。首先,我们讨论在二维绘图中应该怎样做,然后把这个原则扩展到三维图形中。
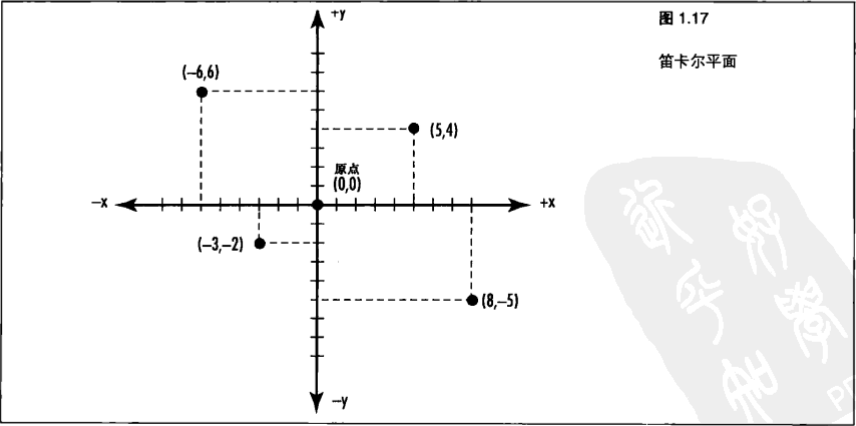
2D 笛卡尔坐标在二维绘图中,最为常用的坐标系统是笛卡尔坐标系统。笛卡尔坐标系统由一个x坐标和一个y坐标构成。
x坐标测量水平方向的位置,而y坐标则测量垂直方向的位置。
笛卡尔坐标系统的原点(Origin)是(x=0, y=0)。笛卡尔坐标用括号内的一个坐标对来表示,第一个是x坐标,第二个是y坐标,中间由一个逗号分隔。例如,原点就写为(0, 0)。
(图1.17)描述了二维的笛卡尔坐标系统,带刻度的x和y线被称为 "轴",可以从负无穷延伸到正无穷。
这张图是我们在学校时经常使用的真实笛卡尔坐标系统。今天,当我们在绘图时指定坐标系统,不同的窗口映射模式可能会导致坐标的解释不一致。在本书后面章节,我们将会看到如何使用不同的方式把真实的坐标控件映射到窗口坐标。
 坐标裁剪
坐标裁剪
窗口时以像素为单位进行度量的。开始在窗口中绘制点、线和形状之前,必须告诉OpenGL如何把指定的坐标翻译为屏幕坐标。
我们可以通过指定占据窗口的笛卡尔控件区域完成这个任务,这个区域称为裁剪区域。
在二维空间中,裁剪区域就是窗口内部最小和最大的x和y值。另一个方法是根据窗口指定原点的位置。
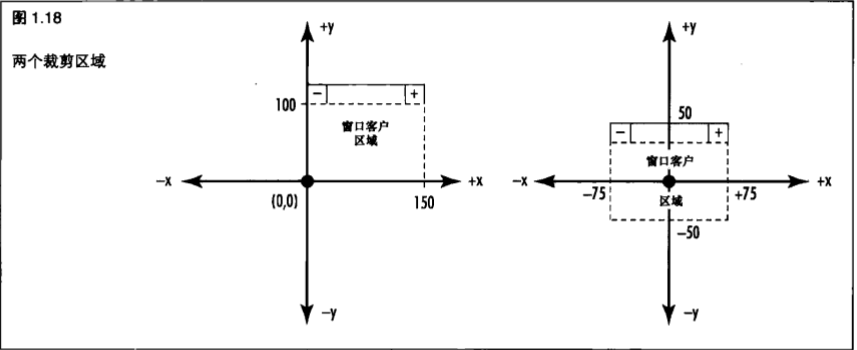
(图1.18)展示了两种常见的裁剪区域。
第一个例子:(图1.18左侧)
窗口x坐标的范围自左向右为 0 到 +150, y坐标的范围从上而下为 0 到 +100,屏幕正中的点用(75, 50)来表示。
第二个例子:(图1.18右侧)
窗口x坐标的范围自左向右为 -75 到 +75, y坐标的范围从上而下为 -50 到 +50,屏幕正中的点用原点(0, 0)来表示。
当然我们还可以使用OpenGL函数(或用于GDI绘图的普通Window函数)上下反转或左右反转坐标系统。
事实上,在Window窗口的默认映射中,坐标的y的值始终为正,并且从上而下递增(Win32就是这样的)。
这种默认的映射模式在自上而下绘制文本时非常有用,但在绘制图形时则显的不太方便。
裁剪区域的宽度和高度很少正好与窗口的宽度和高度(以像素为单位)相匹配。
因此,坐标系统必须从逻辑笛卡尔坐标映射到物理屏幕像素坐标。这个映射是通过一种叫做视口(Viewport)的设置来指定的。
视口就是窗口内部用于绘制裁剪区域的客户区域。视口简单地把裁剪区域映射到窗口中的一个区域。
通常,视口被定义为真个窗口,但这并非严格必须的。例如,我们可能只希望窗口下半部分进行绘图。
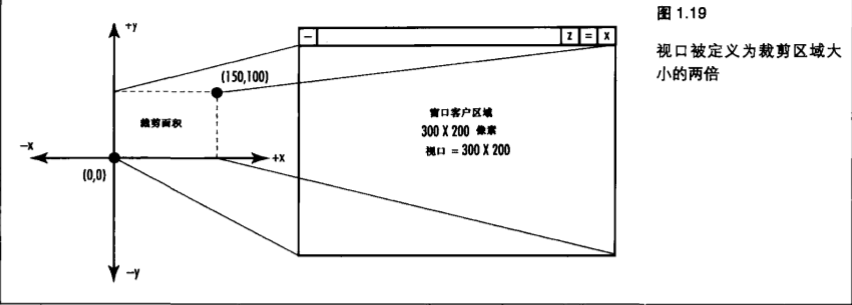
(图1.19)所示是个很大的窗口,其大小为300x300像素,它的视口被定义为整个用户区域。
如果这个窗口的裁剪区域被设置为沿x轴 0 至 150,沿 y 轴 0 至 100,我们所看到这个窗口的逻辑坐标将被映射到一个更大的屏幕坐标系统中(因为裁剪区域比视口小)。
逻辑坐标系统的每个增量将与窗口物理坐标系统(像素)的两个增量相匹配。
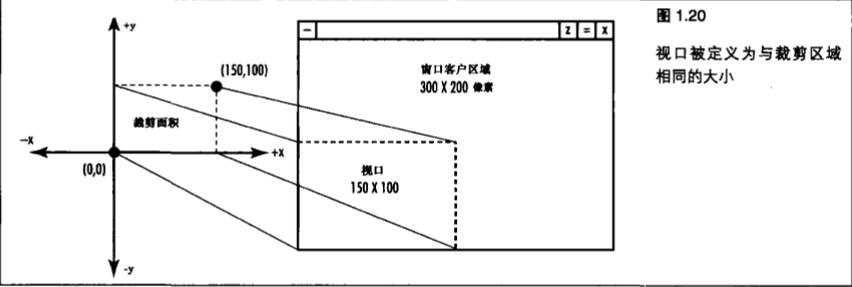
与此形成对比的是,(图1.20)展示了一个与裁剪相匹配的视口。我们所看到的这个窗口仍然是300x200像素。但是现在可视区域将占据窗口的左下部分。
我们可以使用视口来缩小或放大窗口中的图像,也可以通过把视口设置为大于窗口的用户区域,从而只显示裁剪区域的一部分。
 顶点-----空间中的一个位置
顶点-----空间中的一个位置
在2D和3D中,当我们绘制一个物体时,实际上都是用一些更小的称为图元(Primitives)(点,线)的形状来组成这个物体。
图元是一维或二维的实体或表面,如点、直线和多表现(平面多变的形状)。
在3D空间中,我们把图元组合在一起创建3D物体。例如一个三维立方体是由6个二维的正方形组成,每个正方形代表一个独立的面。
正方形(或其他任何图元)的每个角称为顶点(Vertex)。这些顶点就在3D空间中指定了一个特定的坐标。
顶点其实也就是2D或3D空间的一个坐标。创建实体3D几何图形其实不过就是一种连线游戏罢了。
我们将在第3章讨论所有的OpenGL图元以及如何使用它们。
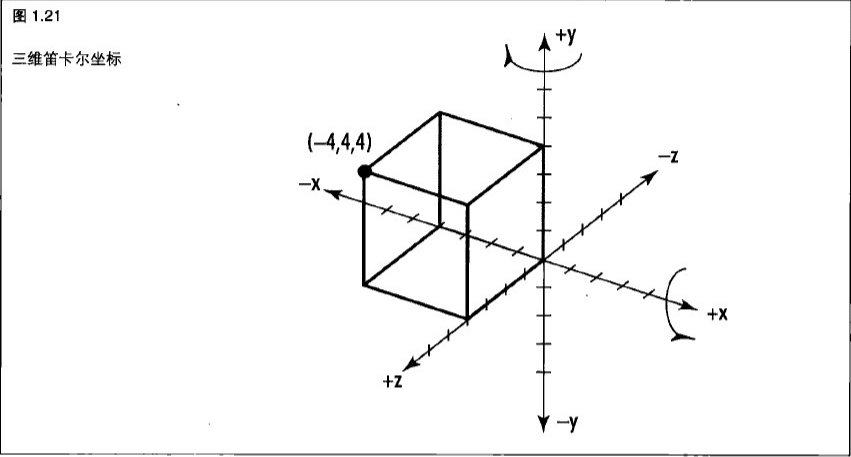
3D 笛卡尔坐标现在,我们把二维坐标系统扩展到三维空间中,并增加深度分量(Depth)。
(图1.21)所示的笛卡尔坐标系统增加了一个新的轴:Z轴。Z轴同时垂直于x轴和y轴。
它代表了一条从屏幕的中心朝向读者的直线(我们已经旋转了这个坐标系统的视角,把y轴向左旋转,把x轴向下和后旋转)。
否则,Z轴将直接面向我们,我们将无法看到Z轴。现在我们用3个坐标(x, y, z)来指定一个三维空间的一个位置。
例如:(图1.21)所示的一个点(-4, -4, -4)。
我们已经知道如何在3D空间使用笛卡尔坐标来表示位置。
但是,不管我们觉得自己的眼睛所看到的三维图像有多么真实,屏幕上的像素实际上只是二维的。
那么OpenGL是如何把这些笛卡尔坐标翻译为可以在屏幕上绘图的二维坐标呢?
简而意之,答案就是 "三角法和简单的矩阵操纵"。
简单?
事实上或许并非如此,但是如果我们花很长的篇幅来讨论其中的概念,我们很可能会失去很多对这些细节不感兴趣的读者。
(第4章我们将对此稍做讨论,至于更深入的讨论,读者可以参考附录A "更多阅读建议" 中的参考部分)
幸运的是,当我们使用OpenGL创建图形时,并不需要对数学有深入的理解。但是,我们在这方面的造诣越深,能够利用OpenGL所发挥的威力也就越大。
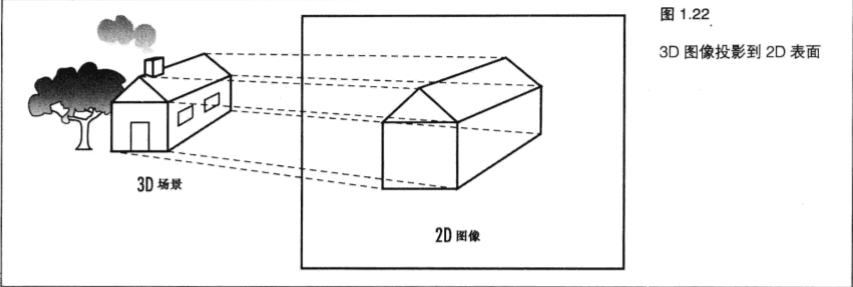
我们真正需要理解的第一个概念称为投影(Projection)用于创建集合图形的3D坐标将投影到一个2D表面(窗口背景)。(如图1.22)
在OpenGL中,绝大多数情况下,我们所关心的两种主要类型的投影。
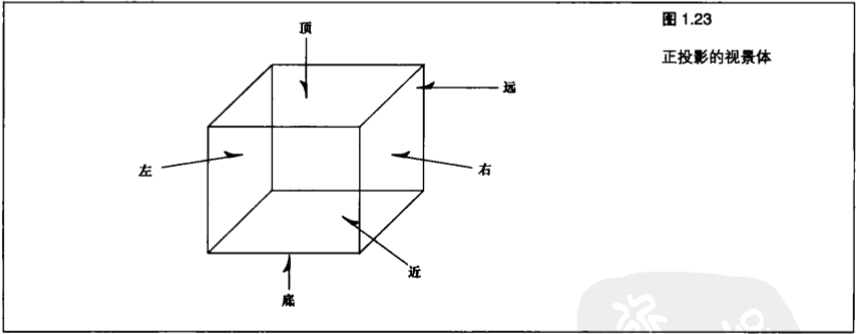
第一种称为正投影(Orthographics Projection)或平行投影。
使用这种投影时,我们需要指定一个正方形或长方形的视景体。
视景体之外的任何物体都会被绘制。而且所有实际大小相同的物体在屏幕上都具有相同的大小,不管他们是远或是近。
这种类型的投影(图1.23)最常用于建筑设计、计算机辅助设计或2D图形中。
此外,在3D图形场景中,我们也常常需要使用正投影,在场景的顶部添加文本或者2D覆盖图。(游戏的GUI)
 透视投影
透视投影
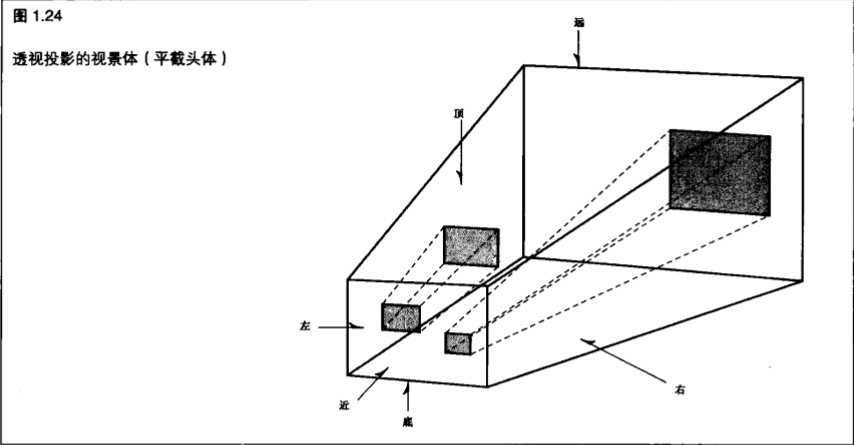
第二种投影是透视投影(Perspective Projection),它更为常见。
在这种投影中,远处的物体看上去比近处的物体更小。他的视景体(图1.24)看上去有点像一个顶部被削平的金字塔。
剩下来的这个形状称为平截头体(Frustum)。靠近视景体的物体看上去比较接近它们的原始大小。但是,当靠近视景体后部的物体将被 投影到视景体的前部时,套门看上去就显的比较小。在模拟和3D动画中,这种投影能够获得最大程度的逼真感。
本书的所有示例源码将放到Github中,详细地址:Github-OpenGL-Example
本章的BLOCK的示例源码详细地址:Github-BLOCK
作者:南雨兮