预测问题评价指标：MAE、MSE、R-Square、MAPE和RMSE

Jenna ·

更新时间:2024-11-15

· 787 次阅读

MAE、MSE、R-Square、MAPE和RMSE

以上是对于预测问题的评价指标。

1.平均绝对误差（Mean Absolute Error, MAE）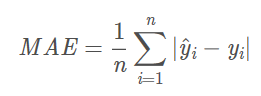

在这里插入图片描述
误差越大，该值越大。

2.均方误差（Mean Squared Error, MSE）

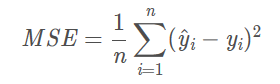
在这里插入图片描述
误差越大，该值越大。

SSE(和方差)与MSE之间差一个系数n，即SSE = n * MSE，二者效果相同。

3.均方根误差（Root Mean Square Error, RMSE）

是MSE的算数平均根
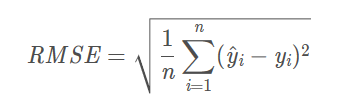
在这里插入图片描述
误差越大，该值越大。

4.平均绝对百分比误差（Mean Absolute Percentage Error, MAPE）

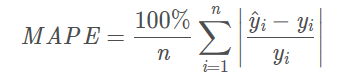在这里插入图片描述注意：当真实值有数据等于0时，存在分母0除问题，该公式不可用。

5.确定系数（R-Square or R2）

首先，残差平方和为：
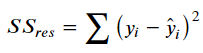
在这里插入图片描述
总平均值为：

得到R2表达式为：

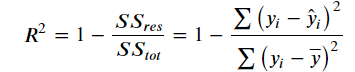
R2用于度量因变量的变异中可由自变量解释部分所占的比例，取值范围是 0~1，R2越接近1,表明回归平方和占总平方和的比例越大,回归线与各观测点越接近，用x的变化来解释y值变化的部分就越多,回归的拟合程度就越好。
所以R2也称为拟合优度（Goodness of Fit）的统计量。

yi表示真实值，y^i表示预测值，y¯i表示样本均值。得分越高拟合效果越好。

代码如下：

import numpy as np
from sklearn import metrics
# MAPE需要自己实现
def mape(y_true, y_pred):
    return np.mean(np.abs((y_pred - y_true) / y_true))
y_true = np.array([1.0, 5.0, 4.0, 3.0, 2.0, 5.0, -3.0])
y_pred = np.array([1.0, 4.5, 3.8, 3.2, 3.0, 4.8, -2.2])
# MSE
print('MSE:',metrics.mean_squared_error(y_true, y_pred)) # 0.2871428571428571
# RMSE
print('RMSE:',np.sqrt(metrics.mean_squared_error(y_true, y_pred))) # 0.5358571238146014
# MAE
print('MAE:',metrics.mean_absolute_error(y_true, y_pred)) # 0.4142857142857143
# MAPE
print('MAPE:',mape(y_true, y_pred)) # 0.1461904761904762

## R2-score
from sklearn.metrics import r2_score
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
print('R2-score:',r2_score(y_true, y_pred)) # 0.9486081370449679

参考文章：
https://blog.csdn.net/guolindonggld/article/details/87856780

作者：条件反射104

mse

1024 个赞