密码学基础(1)
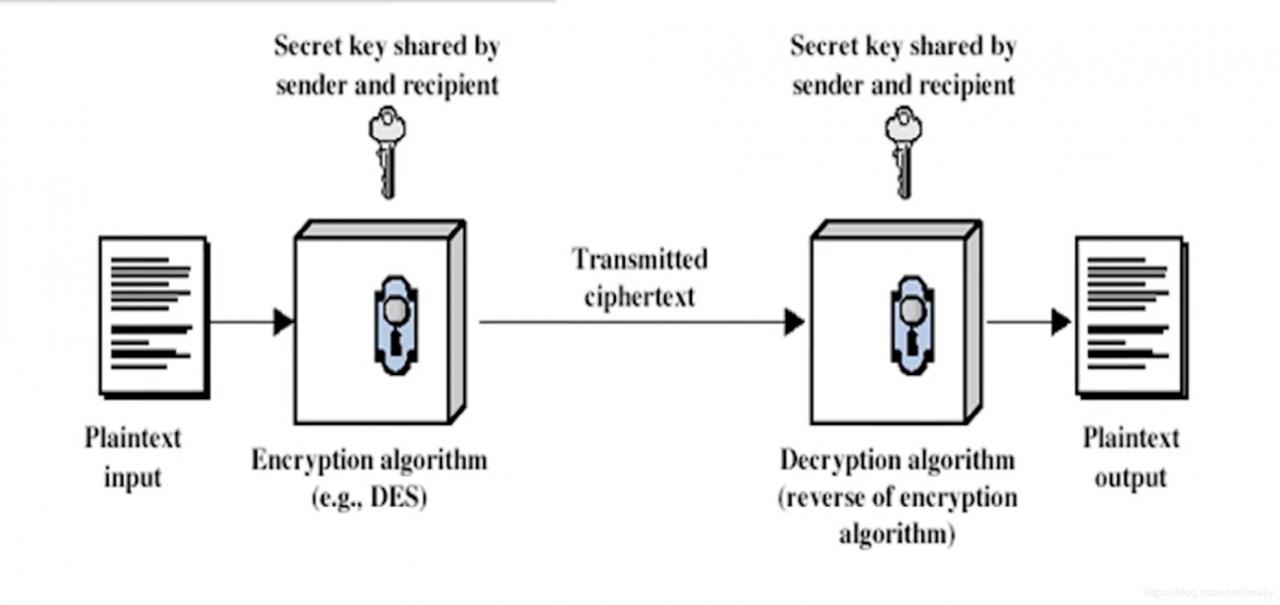
一、对称密钥密码系统
- 在图像、视频、声音以及文本中隐藏信息。 数字水印 二、公开密钥密码系统
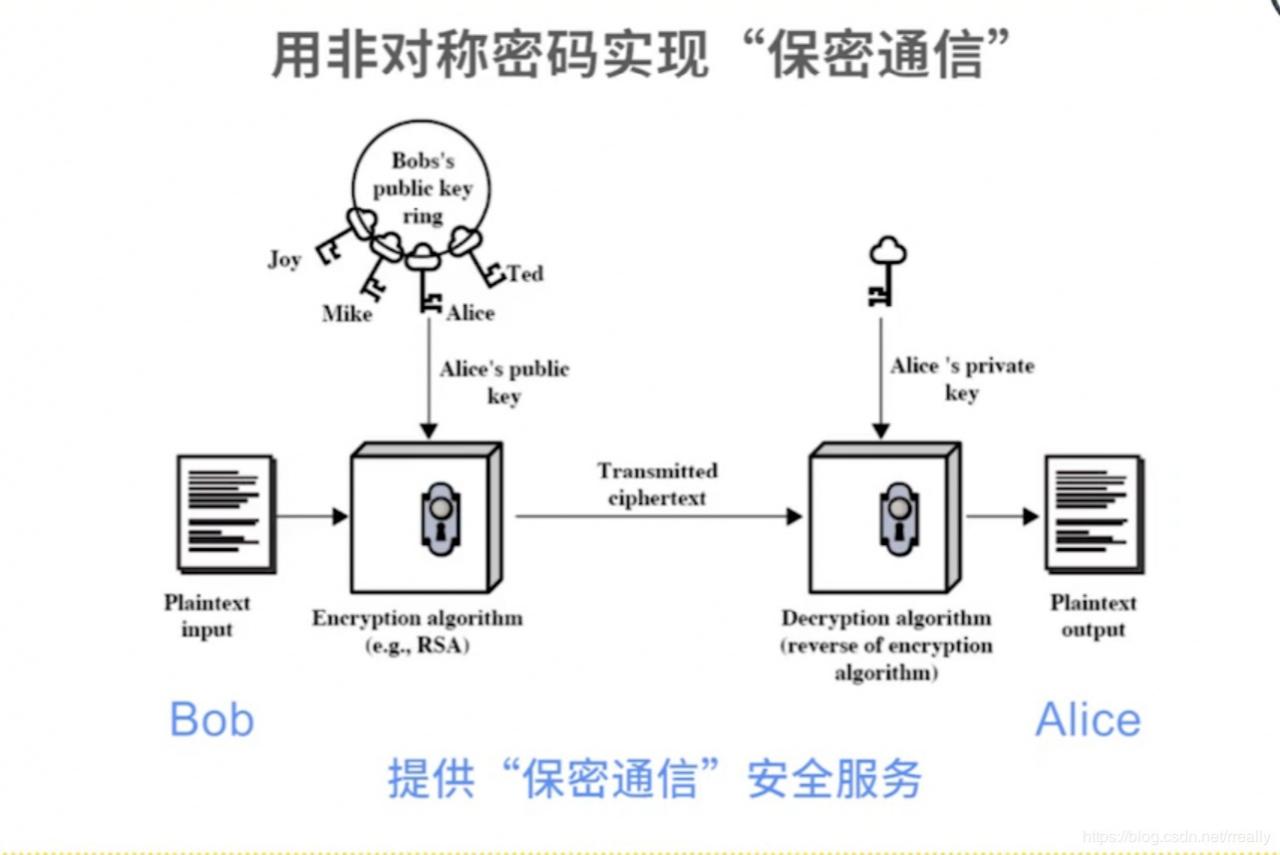
可交换使用:用公钥加密的可以用私钥解密,用私钥加密的可以用公钥解密。
作者:rreally
发送方加密与解密方解密使用同一个密钥,密钥是事先双方共享的秘密。
明文 P
密文 C
密钥 K
加密算法 E:M*K->C
解密算法 D:C*K->M
所有密码全部寓于密钥
凯撒密码 明文 p 密文 C 密钥 k 加密算法 C=E( p )=( p+k )mod(26) 解密算法 p=D( C )=( C-k )mod(26)
playfair: 2字节加密(26*26表格进行单字母分析)
维吉尼亚密码: 26*26字母表(密钥循环使用,具有周期性)
autokey cipher : 自动生成密钥(密钥长度和明文一样长)(可以被密码分析【用统计学方法破解】)
vernam密码: 用随机密钥加密明文
One-Time Pad :
Ci=Pi⊕1Ki Pi=Ci⊕Ki 乘积密码: 由于单次密码并不安全,所以经常使用多次叠加。转子机:
拥有多个转盘共26^n个字母表。
古典隐写术:藏头诗、隐写墨水等。
信息隐藏技术: 伪装式保密通信- 在图像、视频、声音以及文本中隐藏信息。 数字水印 二、公开密钥密码系统
每个人拥有两个密钥
公钥,Public key -——公开。
私钥,Private key——保密。
可用于对称密钥的交换。
可交换使用:用公钥加密的可以用私钥解密,用私钥加密的可以用公钥解密。

用私钥加密可以进行身份认证(数字签名)。
RSA生成两个大素数(百位数字以上)p和q,
计算乘积n=pq并计算小于 n的互质素数个数φ(n)=(p-1)(q-1),并随机生成一个小于φ(n)的数字e,且e与φ(n)互质,通过e*d=1 mod φ(n)求出d,并将d保密销毁q和p公开n和e。
得出:
公钥公开 :PU={e,n}
私钥保密 :PR={d,n}
加密算法
获取公钥后,计算
C=Me mod n(0<M)。
M=Cd mod n。
公钥密码的算法基础单向函数:基本含义是已知x易求y,但已知y难得出x的函数。
Diffie-Hellman通信双方选择一个大素数p以及p的原根a
用户A随机Xa<p,计算Ya=a^Xa^ mod p
用户B随机Xb<p,计算Yb=b^Xb^ mod p
大家保密X,将Y值交换,即X为私钥,Y为公钥。
由A⊕B=C可推出A⊕C=B和B⊕C=A。 ↩︎
作者:rreally