the deep ritz method论文梳理
《The Deep Ritz Method: A Deep Learning-Based Numerical Algorithm for Solving Variational Problems》
Abstract本文提出了一种基于深度学习的deep ritz方法,该方法用于数值求解变分问题,特别是偏微分方程引出的变分问题。deep ritz是非线性,也可是自适应的(一直不太懂自适应),而且很有可能在相当高维的空间也可以work。这个框架很简单,而且适用于深度学习中的随机梯度下降法。
Deep Ritz Method 1.问题分析(1)变分问题

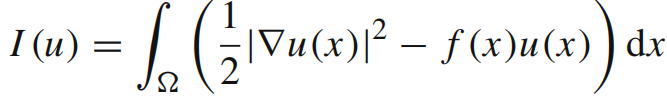 H表示试函数集合(这个试函数集合中包含变分问题的解);f是一个给定的函数,表示所考虑系统的外力
H表示试函数集合(这个试函数集合中包含变分问题的解);f是一个给定的函数,表示所考虑系统的外力
这类问题在物理学中十分常见
(2)deep ritz method基于以下一系列想法:
a. 基于深度神经网络,逼近试函数
b. 函数的一个数值积分规则
c. 求解最后优化问题的一个算法
(1)神经网络结构如下:
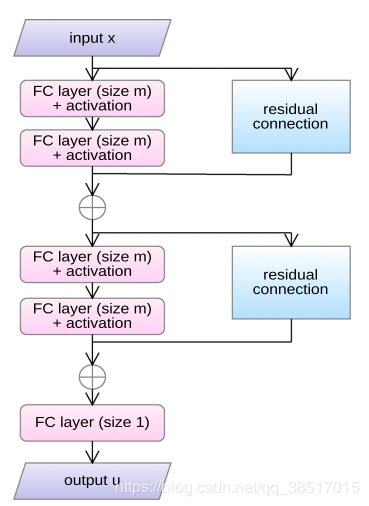
(2)网络由多块组成,每块包括两个全连接层,和一个残差连接
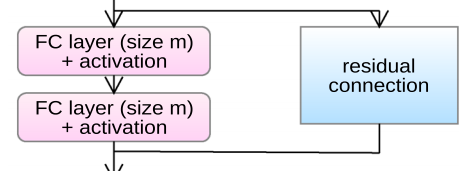
每一块的输入是s,输出是t,s和t都是m维的向量,每一块的公式如下: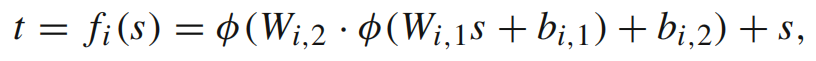
![]()
![]()
(3)整个网络的最终输出: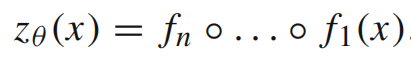
构造试函数,即变分问题的解
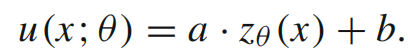
把上式代入1中的变分问题,得到以下的优化问题–即loss函数:
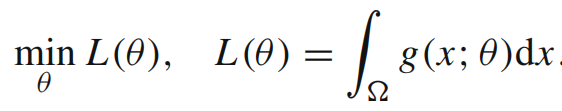
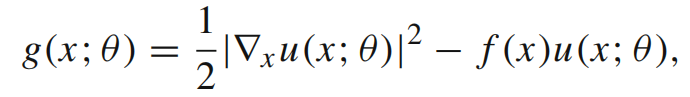
(1)优化问题和SGD
优化问题通常是如下形式:
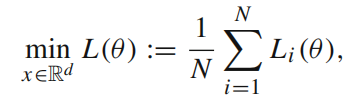 等式右边的每一项对应一个数据点。N是数据点的个数,通常很大。
等式右边的每一项对应一个数据点。N是数据点的个数,通常很大。
用随机梯度下降法求解这个优化问题
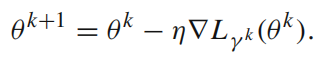 L的下标是在{1,2,3,…,N}上均匀分布的随机变量
L的下标是在{1,2,3,…,N}上均匀分布的随机变量
SGD的关键点是:在计算L的梯度时,不是计算总和,而是随机选取和中的某一项
而实际中,每一次迭代,不是只选择一项,而是一个mini-batch
(GD,BGD,SGD,MBGD)
(2)积分的离散化
把积分看作连续和,区域上的每个点成为数据点
因此,在SGD迭代的每一步,可以选择一个mini-batch离散化积分,mini-batch中的点随机选取,在每个点上使用相同的积分权重
注意:如果我们使用标准的积分规则离散化积分,必然会选择一组固定的点。那么就有可能产生这样的情况:在固定节点的积分最小化了,但是函数本身却没有最小化。那么SGD随机选取一个mini-batch的特性就避免了上面的风险。
此时,SGD公式如下:
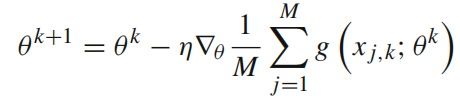
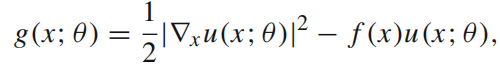 对于第k次迭代,{xj,k}是在区域上根据均匀分布随机采样的一组点
对于第k次迭代,{xj,k}是在区域上根据均匀分布随机采样的一组点
为了加速神经网络的训练,使用SGD的Adam版本。
小结:这里应用到的知识点就是积分的离散化,然后和优化方法SGD统一起来了
关于积分的离散化:类似于积分的定义,选取一些离散点,对每个点求和
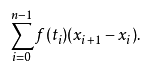
(1)考虑问题:
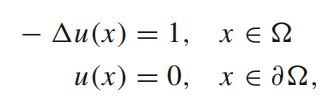
![]()
(2)所用网络
4块(8个全连接层),数出m=10,一共881个参数
(3)边界作惩罚项:
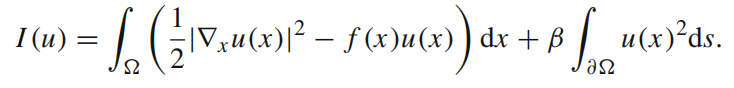
![]()
(4)结果比较
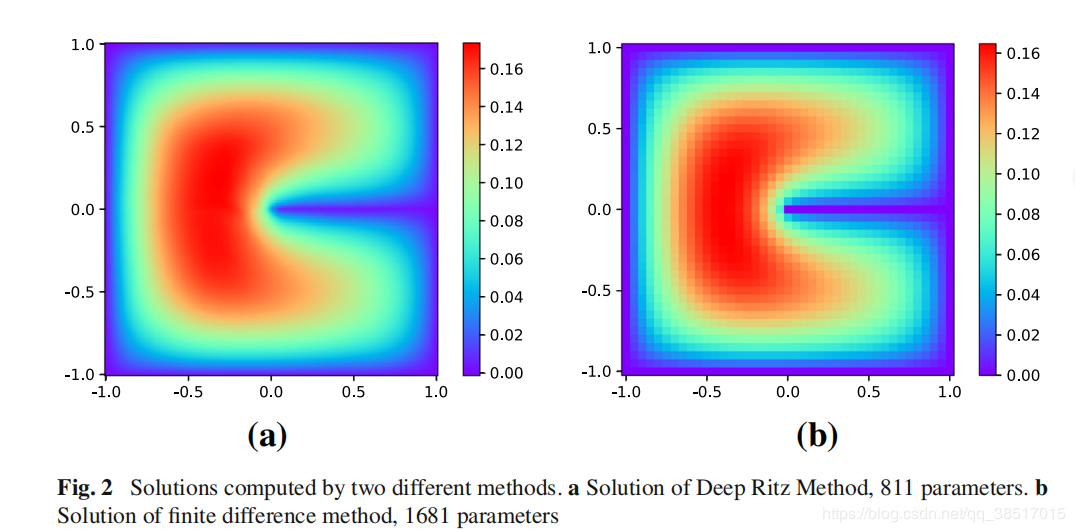 得到的解基本相同
得到的解基本相同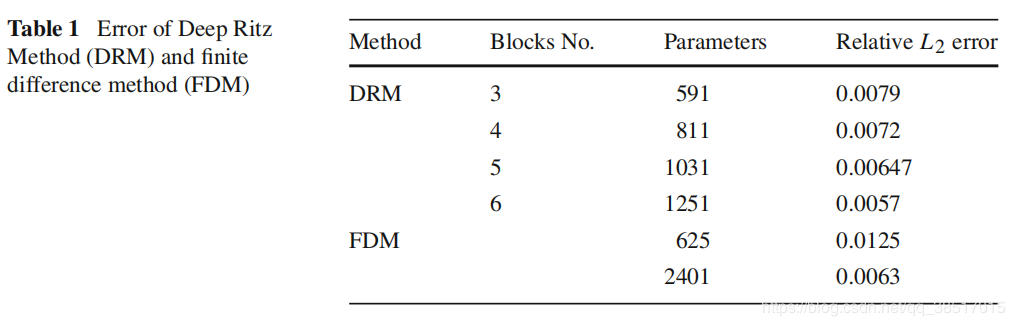 DRM参数较少时,解的精度都比FDM高
DRM参数较少时,解的精度都比FDM高
(1)考虑问题:
维度为10
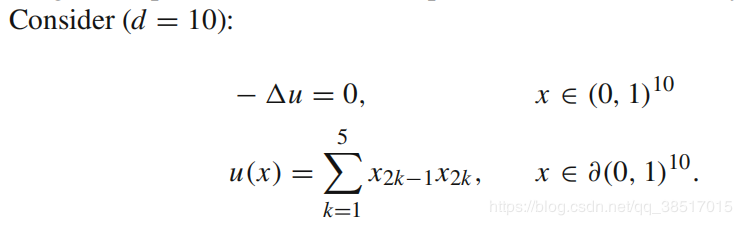
(2)网络
三块(六个全连接层),671个参数,SGD的每一次迭代,从区域中选取1000个点,区域边界选取100个点,惩罚参数为1000
(3)结果
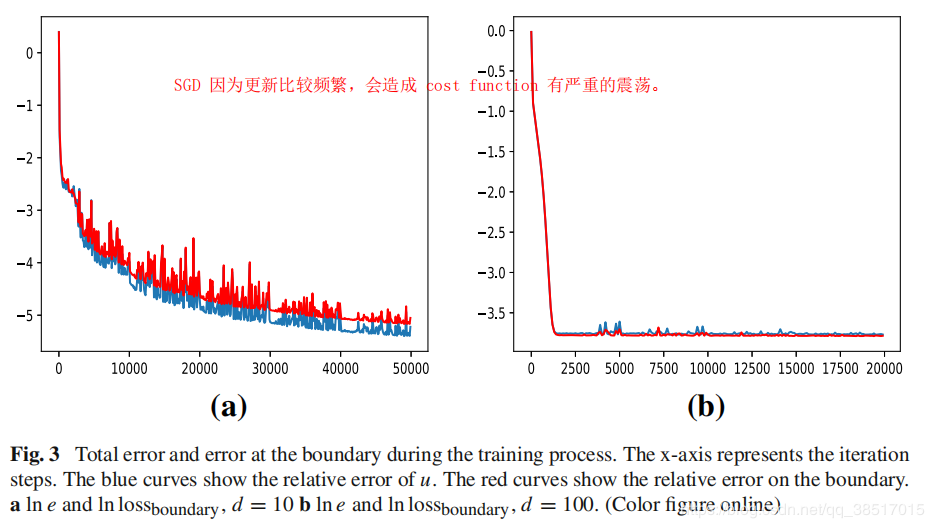
SGD收敛很快;又对每个数据都更新,所以更新很频繁,也因此震荡很严重
作者:Evavava啊