浅谈零知识证明
零知识证明(zero knowledge),顾名思义其实就是在充分证明自己是某种权益的合法拥有者的同时,又不能把有关的信息泄露出去,即提供给外界的有用信息为"零"。
零知识起源"零知识"的概念最早在20世纪80年代初,由麻省理工学院的研究人员Shafi Goldwasser, Silvio Micali和Charles Rackoff所提出,当时这些人正在研究与交互证明系统相关的问题,即一种理论系统,使得甲方(证明者)可以和乙方(验证者)交换信息,并借此说服乙方接受(通过验证)某个数学论述为真。
这个问题并不是单纯的理论思考,而是在真实,具体的应用中会面临到的问题。
我们举个例子,假设你想要使用密码登录网站,标准化的协议流程是这样的:客户端(你)输入密码并发送给服务器,服务器将你的密码进行哈希计算,然后对比存储在服务器端的密码哈希值,如果两者相同,你便能够登录系统。在上述过程中,服务器需要拥有你的密码明文,所以你的隐私能够被保障全看服务器端的脸色,如果服务器受到攻击,甚至被入侵,那么你的密码就会暴露给恶意攻击者,导致严重的后果。
Goldwasser,Micali和Rackoff等人提出的这种全新的方法,如果证明真的可行,那么它将允许我们在证明某些数学陈述为真的同时,保证不会有任何不相关的信息被泄露出去。
零知识证明的特性零知识证明需要满足以下特性:
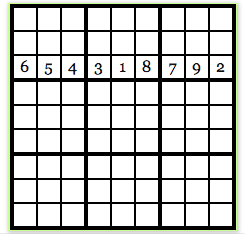
完整性(Completeness):如果论述(注: 这里的”论文“即”零知识证明“中的”知识“)为真,那么诚实的证明者一定能够说服诚实的验证者 可靠性(Soundness):如果证明者不诚实,那么他们无法通过造假来说服验证者接受某论述。 零知识性(Zero-Knowledge):如果论述为真,验证者无法得知论述实际内容是什么。下面我们举个数独的例子来说明零知识证明的特性。首先玩家会得到一个如下的 9✖️9的表格:
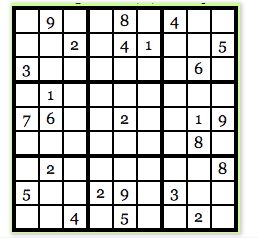
这个游戏的规则是使用1 ~ 9 的数字填满每一行,每一列,及 3 ✖️ 3 的区块,其中数字1 ~ 9 在每一行、每一列、每个3✖️ 3的小区块中都不能重复,前面数独的谜题的解法如下图所示:
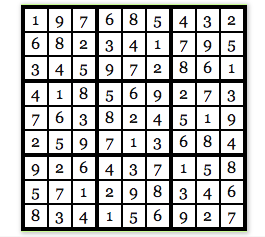
如你所见,每一行、每一列、及每个3✖️3的区块里的数字都是唯一的,没有数字重复。假设现在的Alice已经找到了数独的解,但多疑的Bob不信,他希望Alice能够证明自己的确知道数独的解。Alice要证明自己真的知道,但与之同时,她不希望Bob得到这个数独的解。她该怎么做呢?Alice将使用零知识证明来佐证她的说辞。
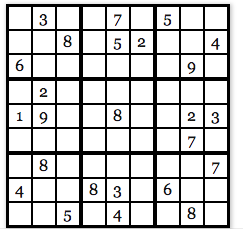
首先,Bob要使用已经被验证过的一个诚实的计算机运行该数独谜题,这个程序会随机选择每个数字的替代码,比如对于这个特定的数独谜题,程序选择了如下的替代码:
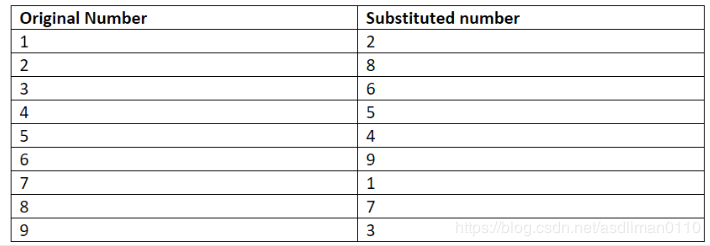
程序选中的替代码使得每个数字都有同样的机会被转换为其他数字。基本上,数字1和数字3倍替换可能性是一样的,数字5和数字7也是如此。因此,根据上面的替代码,我们替换一下上述谜题的解:
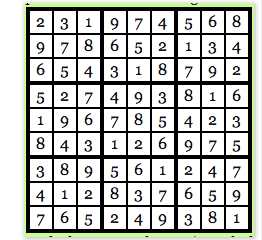
现在Alice拿着这份密码替换表。请注意,此时Bob并不知道初始数独谜题的解是什么,也不知道数字替换表的内容。接着,Alice利用”锁箱机制(lockbox nechanism)“隐藏谜题中所有的数字,因此Bob只能看到一个空白的9✖️9的表格。
现在Bob有28种选择:
显示任一行(9行) 显示任一列(9列) 显示任一 3✖️3的区块(9块) 显示初始谜题的替换后版本假设Bob选择显示第三列,如下图所示:
Bob将会看到这样的画面:每个数字都在该列中唯一出现,又因为初始谜题中每个数字被替换的概率相同,因此Bob无法推出初始谜题的解释什么。
现在假设,Bob决定选择最后一项,即想看看替换后版本的模样,他会看到如下图所示:
同样的,因为替代码是随机选择的,每个数字都有相同的替换概率,Bob将无法得知初始谜题的解。Bob每回都可以从这28种选择中得以进行验证,最终他会相信Alice的论述,即Alice是知道数独的谜题解。
为什么呢?因为如果Alice作弊(她不知道初始谜题的解),她就无法找到完整的替换码,得到Bob的28种选择都有唯一的解,假设Bob只验证了一次,比如他就看了一行,那么Alice作弊的概率高达27/28。但如果Bob进行了多达200次的验证,那么Alice作弊成功的概率就会降到(27/28)^ 200,作弊成功率连0.05%都不到。
接着让我们检查一下,零知识证明特性在这个案例中是否满足:
完整性(Completeness):密码程序经过验证所以可信,而且Alice和Bob都接受这个协议。 可靠性(Soundness):如果做了200次随机测试,那么Alice作弊成功率小于0.05%。 零知识性(Zero-Knowledge):Alice从头到尾都不必向Bob透露初始谜题的解。 零知识证明在区块链中的应用零知识协议支持在分布式区块链网络上转移资产,并具有完全的隐私性。常规的区块链交易,当资产从一方发送到另一方的时候,该交易的详细信息对网络中每一方都可见。相反,零知识证明交易中,其他人只知道发生了有效的交易,但并不知道发送方、接收方、资产类别和交易数量等具体的信息。
最突出使用零知识证明的要数ZCash了,它也是第一个实现zk-Snarks的加密货币。此后,其他区块链系统也加入了零知识证明的行列中,以便在交易进行的过程中,保护用户隐私。其中以以太坊的最为突出,在拜占庭升级的版本中,zk-Snarks作为升级的一部分,正式加入到以太坊未来的开发计划中。
本文小结零知识证明是构建信任的重要技术,也是区块链这个有机体中不可缺少的一环。通过零知识证明,相当于在无形中建立了一个区中心化的第三方机构,避免了可能存在作弊的风险。互联网实现了信息的传递,而集成了零知识证明的区块链,将在信息传递的过程中,保护了每个人的隐私。进一步完善了整个互联网体系,这将在人类走上更高文明的历程中刻下浓墨的一笔。
作者:雨落苏桥