翻译 - ResNet-v2 - Identity Mappings in Deep Residual Networks

  深度残差网络作为一种极深的网络结构，它展现了其极好的准确性和收敛行为。在本文中，我们分析了残差构造块后面的传播公式，表明了当跳跃连接和附加激活都使用恒等映射时，前向和反向信号可以直接从一个块传播到其他任何一个块。通过一系列实验证明了恒等映射的重要性。它激励我们提出了一个新的残差单元，不仅让训练变得更加容易，而且提高其泛化性能。我们汇报了其改进的结果：在 CIFAR−10CIFAR-10CIFAR−10 和 CIFAR−100CIFAR-100CIFAR−100 数据集上使用 100110011001 层 ResNetResNetResNet (4.62% errorerrorerror) ，以及在 ImageNetImageNetImageNet 使用了 200200200 层的 ResNetResNetResNet 。下载代码！

  深度残差网络由多个“残差单元”堆叠而成（ResNetsResNetsResNets）。每个单元都可以表示成一个一般形式：

                yl=h(xl)+F(xl,Wl),y_l=h(x_l)+F(x_l,W_l),yl​=h(xl​)+F(xl​,Wl​),
                xl+1=f(yl),x_{l+1}=f(y_l),xl+1​=f(yl​),

  其中 xlx_lxl​ 和 xl+1x_{l+1}xl+1​ 分别代表第 lll 个单元的输入和输出，FFF 是一个残差函数。在【1】中，h(xl)=xlh(x_l)=x_lh(xl​)=xl​ 是一个恒等映射，fff 是ReLUReLUReLU函数。

  对于深度超过100层的 ResNetsResNetsResNets 在 ImageNetImageNetImageNet 和 MSCOCOMS COCOMSCOCO 比赛的多个挑战识别任务上，展现出极好的准确性。ResNetsResNetsResNets 的中心思想是学习额外的且对应着 h(xl)h(x_l)h(xl​) 的残差函数 FFF，其思想的关键就是使用一个恒等映射 h(xl)=xlh(x_l)=x_lh(xl​)=xl​，这个是通过附加一个恒等跳跃连接所实现的。（快捷连接）

  在本文中，我们不只是在一个残差单元里，而是通过整个网络来建立一个传播信息的 “直连” 路径，来对深度残差网络进行分析。我们的推导表明：如果 h(xl)h(x_l)h(xl​) 和 f(yl)f(y_l)f(yl​) 都是恒等映射，那么无论是前向和反向的传递，信号都可以直接从一个单元传递到另一个单元。我们的实验表明，当框架接近以上两种情况时，训练通常会变得很容易。

  为了理解跳跃连接的作用，我们分析并比较了多种 h(xl)h(x_l)h(xl​) 的类型。我们发现恒等映射 h(xl)=xlh(x_l)=x_lh(xl​)=xl​ 在所有研究的类型中，误差衰减最快，训练误差最低。然而，跳跃缩放连接，门控，1×1 的卷积都导致了更高的训练损失和误差。这些实验表明，一个 “干净” 的信息通道对简化优化时很有帮助的。（在 Fig.1,2,4Fig.1,2,4Fig.1,2,4 中用灰色箭头表示的）

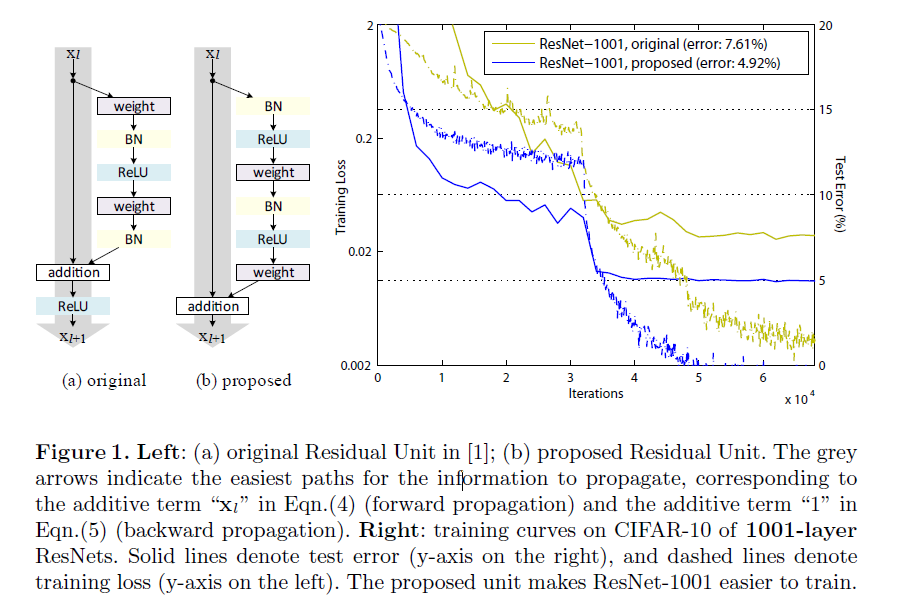
  为了构建一个恒等映射 f(yl)=ylf(y_l)=y_lf(yl​)=yl​，与传统观念的 “后激活” 恰恰相反，我们把激活函数（ReLUReLUReLU、BNBNBN）作为权重层的 “预激活” 。这个观点将会导致一个新的残差单元的设计，在 (Fig.1(bFig. 1(bFig.1(b) 展示。基于这个单元，我们构建了一个 100110011001 层的 ResNet,ResNet,ResNet, 在 CIFAR−10/100CIFAR-10/100CIFAR−10/100 上展示了极具有竞争力的结果，它比【1】中原始的 ResNetResNetResNet 更容易优化并且泛化能力更强 。我们进一步展示了使用 200200200 层 ResNetResNetResNet 在 ImageNetImageNetImageNet 数据集上改进后的结果，但【1】中的部分开始过拟合。这些结果表明，网络深度的维度还有很大的开发空间，这就是现代深度学习成功的关键。

   【1】中的 ResNetsResNetsResNets 是通过将相同连接形状的构造块堆叠的模块化结构。本文我们将这些块称为 “残差单元”，【1】中原始的残差单元执行以下的计算：

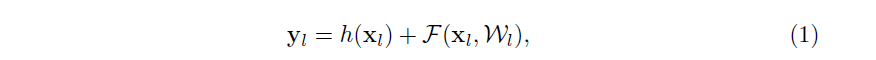
  这里的 xlx_lxl​ 是第 lll 个单元的输入特征，Wl=Wl,k∣1≤k≤KW_l={W_{l,k}|_{1≤k≤K}}Wl​=Wl,k​∣1≤k≤K​ 是与残差单元有关的一组权重（偏置），其中 KKK 是残差单元中的层数（ KKK 是 2 或 3 ）。FFF 代表残差函数，例如：两个 3×3 卷积层的堆叠。函数 fff 是逐元素加后的操作，在【1】中 fff 是 ReLUReLUReLU。函数 hhh 是被作为恒等映射：h(xl)=xlh(x_l)=x_lh(xl​)=xl​。

  如果 fff 也是一个恒等映射：xl+1≡ylx_{l+1}≡y_lxl+1​≡yl​，那么 我们可以将等式（2）代入等式（1）中，得到：xl+1=f(yl)=yl=h(xl)+F(xl,Wl)=xl+F(xl,Wl)x_{l+1}=f(y_l)=y_l=h(x_l)+F(x_l,W_l)=x_l+F(x_l,W_l)xl+1​=f(yl​)=yl​=h(xl​)+F(xl​,Wl​)=xl​+F(xl​,Wl​)

  递归地的计算，我们将会得到：

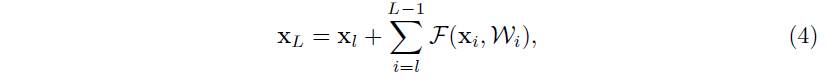
  对于任何深层单元 LLL 和浅层单元 lll，Eqn.(4)Eqn.(4)Eqn.(4) 展示一些新特性：（i）任何深层单元 LLL 的特征 xLx_LxL​ （都可以被表示为）== 任何浅层单元 lll 的特征 xlx_lxl​ （加上）+ 一个形如 Σi=lL−1FΣ^{L-1}_{i=l}FΣi=lL−1​F 的残差函数，这表明了任何单元 LLL 和 lll 都具有残差特性。（ii）xL=x0+Σi=0L−1F(xi,Wi)x_L=x_0+Σ^{L-1}_{i=0}F(x_i,W_i)xL​=x0​+Σi=0L−1​F(xi​,Wi​) ，对于任意深层单元 LLL，它的特征就是之前所有残差单元输出的总和（再加上 x0x_0x0​）。这与 ”普通网络“ 正好相反，普通网络的特性 xLx_LxL​ 是一系列矩阵向量的乘积，即 Πi=0L−1Wix0Π^{L-1}_{i=0} W_ix_0Πi=0L−1​Wi​x0​，（忽略了 BNBNBN 和 ReLUReLUReLU）。

  Eqn.(4)Eqn.(4)Eqn.(4) 也带来了好的反向传播特性。将损失函数表示为 εεε，从反向传播的链式法则中我们得出：

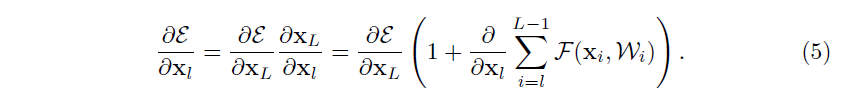
  Eqn.(5)Eqn.(5)Eqn.(5) 表明了梯度 ∂ε∂xl\frac {∂ε}{∂x_l}∂xl​∂ε​ 可以被分解成两个附加项：一项是 ∂ε∂xL\frac {∂ε}{∂x_L}∂xL​∂ε​ 可以不涉及任何权重层就可以直接传递信息，并确保信息直接传回给任意浅层单元 lll。另一项是 ∂ε∂xL(∂∂xlΣi=lL−1F)\frac {∂ε}{∂x_L}(\frac {∂}{∂x_l}Σ^{L-1}_{i=l}F)∂xL​∂ε​(∂xl​∂​Σi=lL−1​F) 通过权重层进行传递。Eqn.(5)Eqn.(5)Eqn.(5) 表明了在一个 mini−batchmini-batchmini−batch 中梯度 ∂ε∂xl\frac {∂ε}{∂x_l}∂xl​∂ε​ 是不可能消失的，因为通常对于全部样本项 ∂∂xlΣi=lL−1F\frac {∂}{∂x_l}Σ^{L-1}_{i=l}F∂xl​∂​Σi=lL−1​F 不可能总为 −1-1−1。这就意味着，即使当权重任意小时，也不会出现层梯度消失的情况。

  Eqn.(4)Eqn.(4)Eqn.(4) 和 Eqn.(5)Eqn.(5)Eqn.(5) 表明无论时前向还是反向传递，信号都可以直接从一个单元传递到另一个单元。Eqn.(4)Eqn.(4)Eqn.(4) 的基础是两个恒等映射：（i）恒等跳跃连接 h(xl)=xlh(x_l)=x_lh(xl​)=xl​（ii）fff 是恒等映射。

  这些直接传递信息流如 Fig.1,2,4Fig.1,2,4Fig.1,2,4 灰色箭头所示。当这些灰色箭头没有覆盖任何操作（除了加法）时，上述两个条件就是正确的，也就是干净的通道。在以下两个章节中，我们将分别研究两个条件的影响。

  进行一个简单的修改，h(xl)=λlxlh(x_l)=λ_lx_lh(xl​)=λl​xl​ 去替代恒等映射：

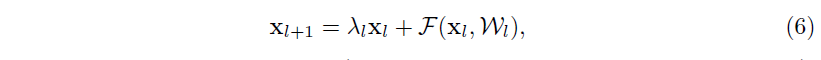
  其中 λlλ_lλl​ 是一个调节标量（为了简单起见，我们仍假设 fff 是一个恒等映射），通过递归地应用这个公式，我们可以获得类似于 Eqn.(4)Eqn.(4)Eqn.(4) 的一个等式：


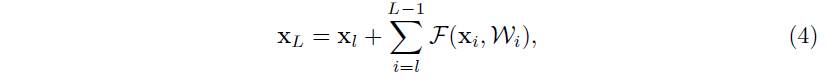
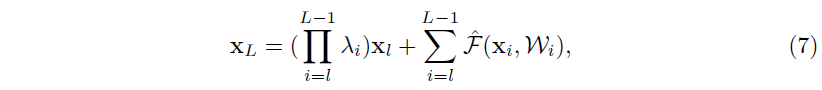
  其中标识 F^\hat FF^ 表示将这些标量放入残差函数中，类似于 Eqn.(5)Eqn.(5)Eqn.(5) ，以下形式为反向传播过程：

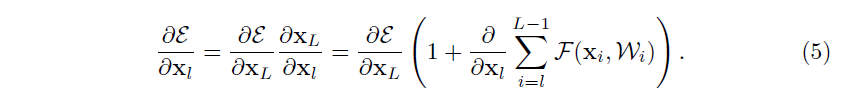
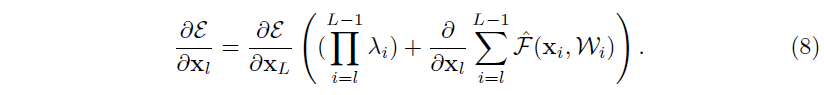
  和 Eqn.(5)Eqn.(5)Eqn.(5) 不同，Eqn.(8)Eqn.(8)Eqn.(8) 的第一项是由 Πi=lL−1λiΠ^{L-1}_{i=l} λ_iΠi=lL−1​λi​ 来进行调节。对于一个极深网络（LLL 很大），如果对于所有的 iii 都有 λi>1λ_i > 1λi​>1 ，这一项将会以指数型放大；如果对于所有的 iii 都有 λi<1λ_i < 1λi​<1 ，这一项将会以指数型缩小甚至消失，它将会阻断从快捷连接返回的信号，并且迫使它流向权重层。如实验结果所示，这个将会导致优化困难。

  我们的实验使用 110110110 层 ResNetResNetResNet 在 CIFAR−10CIFAR-10CIFAR−10 上进行的。这个极深的 ResNet−110ResNet-110ResNet−110 有 545454 个两层残差单元（由 3×3 卷积层组成），这对优化而言是一个挑战。我们的实现细节（见附录）与【1】是相同的。在本篇论文中，我们对 CIFARCIFARCIFAR 上的每个体系进行 555 次运行得到准确率，并取其中位数，便于去避免随机变量所带来的影响。

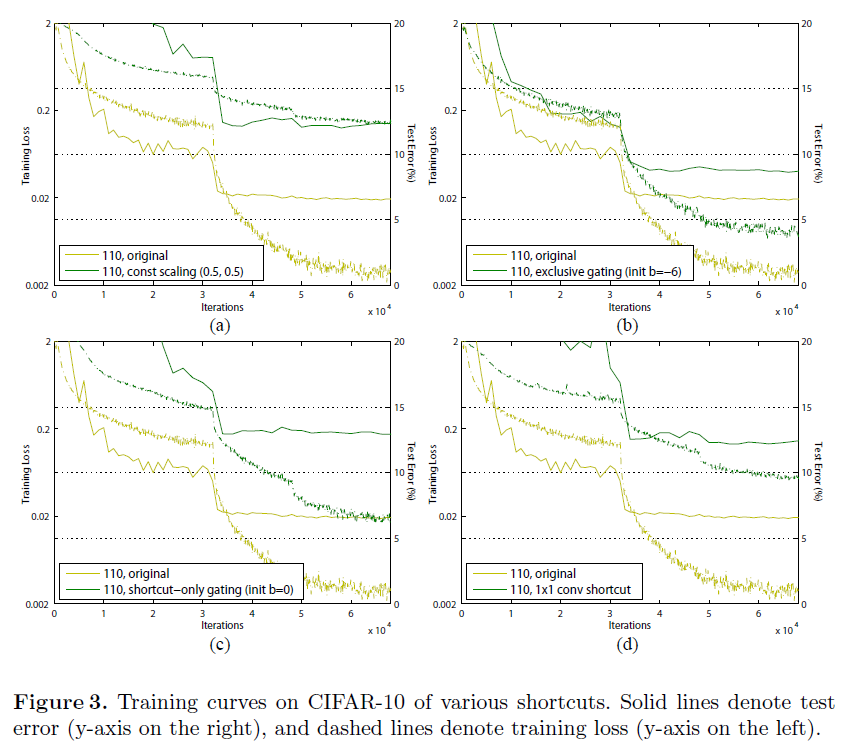
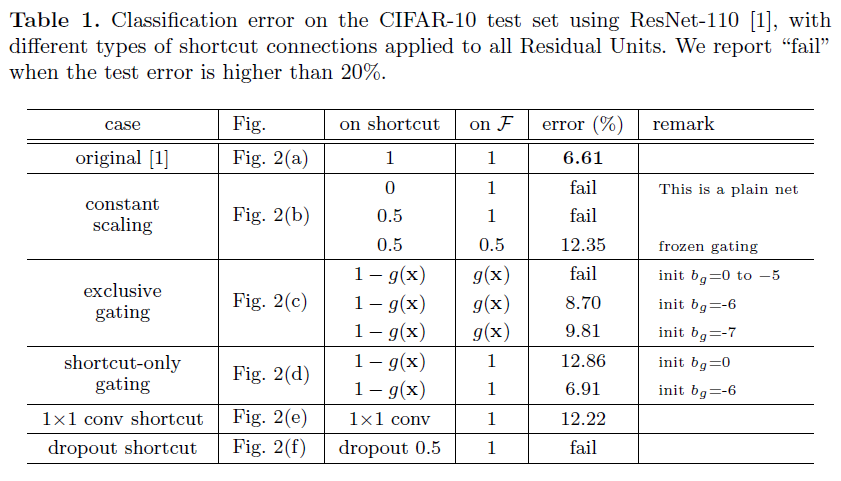
  我们以上的分析是由当 fff 为恒等映射时得到的，但是本节实验都是基于 f=ReLUf=ReLUf=ReLU，我们在下一节解决了恒等映射 fff。我们的基础架构 ResNet−110ResNet-110ResNet−110 在测试集上有 6.616.616.61% 的错误率，与其他变形(Fig.2(Fig. 2(Fig.2 和 Table1)Table 1)Table1)进行比较，总结如下：

  我们为 (Fig.2(b))(Fig. 2(b))(Fig.2(b)) 中所有的快捷连接设置 λ=0.5λ=0.5λ=0.5，我们进一步学习 FFF 的两种缩放情况：（i）FFF 并不会被缩放（ii）FFF 被常数标量 1−λ=0.51-λ=0.51−λ=0.5 进行缩放，类似于 highwayhighwayhighway gatinggatinggating，但是它有冷冻门控。其中第一种情况并不能够很好的收敛，第二种情况可以收敛，但是测试误差实质上比原始的 ResNet−110ResNet-110ResNet−110 更高。Fig3(a)Fig 3(a)Fig3(a) 展示了训练误差要比原始的 ResNet−110ResNet-110ResNet−110 高，表明了当恒等连接被缩放时优化变得更加困难。

  根据采用了门机制的 HighwayHighwayHighway NetworksNetworksNetworks，我们设计了一个门控函数 g(x)=σ(Wgx+bg)g(x)=σ(W_gx+b_g)g(x)=σ(Wg​x+bg​)，由权重 WgW_gWg​ 、偏置项 bgb_gbg​ 和 sigmoidsigmoidsigmoid 函数 σ(x)=11+e−xσ(x)=\frac {1}{1+e^{-x}}σ(x)=1+e−x1​ 组成了一个函数转换。在一个卷积层网络中， g(x)g(x)g(x) 由 1×1 的卷积层来实现的，门控函数由逐元素乘法来调节信号。

  我们对【6,7】的 exclusiveexclusiveexclusive gatesgatesgates 进行研究，FFF 是由 g(x)g(x)g(x) 进行缩放，快捷连接时由 1−g(x)1-g(x)1−g(x) 进行缩放。如 Fig2(c)Fig 2(c)Fig2(c) 所示，我们发现偏置项 bgb_gbg​ 的初始化对于训练门控模型至关重要。通过交叉验证，我们对 bgb_gbg​ 的初始值在 [0，−10][0，-10][0，−10] 之间进行超参数搜索，且在训练集上参数递减量为 −1-1−1。使用最佳值（在这是 −6-6−6 ）在训练集上训练，得到了最好的测试结果 8.708.708.70% (Table1)(Table 1)(Table1)，但仍然远远落后于 ResNet−110ResNet-110ResNet−110 的基准。Fig3Fig 3Fig3 展示其训练曲线。Table1Table 1Table1 记录了使用其他初始化值所对应的实验结果，注意到了当 bgb_gbg​ 并没有适当初始化时， exclusiveexclusiveexclusive gatesgatesgates 网络将不会收敛到一个好的解决方案。

  独控门机制的影响是双面的。当 1−g(x)1-g(x)1−g(x) 接近 1 时，门控快捷连接更接近于恒等快捷连接，这更有助于信息的传递；但是，当 g(x)g(x)g(x) 接近 0 时，抑制了函数 FFF。为了去避免门控函数在快捷连接中的影响，我们接下来研究non−exclusivenon-exclusivenon−exclusive gatesgatesgates 。

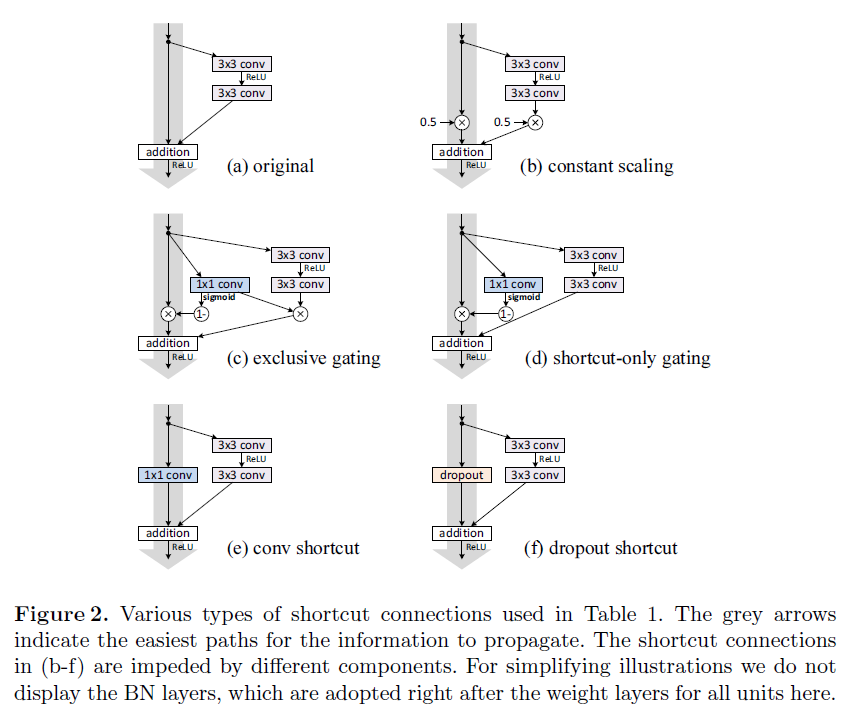
  在这个情况下，函数 FFF 不进行缩放；只有快捷连接由 1−g(x)1-g(x)1−g(x) 进行缩放。如 Fig2(d)Fig 2(d)Fig2(d) 所示，bgb_gbg​ 的初始值仍然是必要的。当 bgb_gbg​ 的初始值是 000 （所以 1−g(x)1-g(x)1−g(x) 最初就是 0.50.50.5），网络收敛得到一个很差的结果 12.8612.8612.86% (Table1)(Table 1)(Table1)，这也是由高训练误差造成的 Fig3(c)Fig 3(c)Fig3(c)。

  当初始值 bgb_gbg​ 是一个负数（例如：−6-6−6），那么 1−g(x)1-g(x)1−g(x) 就会更接近 111，快捷连接也会更接近恒等映射。因此，结果 (6.91(6.91(6.91%, Table1)Table 1)Table1) 更接近原始的 ResNet−110ResNet-110ResNet−110。

  接下来我们用 1×1 的卷积快捷连接来取代恒等快捷连接去进行实验。这个方案已经在【1】（optionoptionoption CCC）中使用 343434 层 ResNetResNetResNet（16个残差单元），并且得到了好的结果，表示 1×1 的快捷连接是有效果的。但是我们发现当有很多残差单元时，情况就变得不一样了。当使用1×1 的卷积快捷连接时，110110110 层的 ResNetResNetResNet 得到了一个更差的结果(12.22(12.22(12.22%, Table1)Table 1)Table1) 。同样地，训练误差变得更高 (Fig3(d))(Fig 3(d))(Fig3(d))。当堆叠了很多残差单元时（为 ResNet−110ResNet-110ResNet−110 堆叠了54个），甚至是最短的路径也仍然会阻碍信号的传播。当使用我们 1×1 的卷积快捷连接在 ImageNetImageNetImageNet 上用 ResNet−101ResNet-101ResNet−101 也看到了相似的现象。

  最后，我们使用 dropoutdropoutdropout （比率为0.5）进行实验，并且对恒等于映射的输出 (Fig.2(f))(Fig. 2(f))(Fig.2(f)) 采用该方法。网络并没有收敛得到一个好的结果， DropoutDropoutDropout 在统计上强加了一个 λλλ 的范围，并且在快捷连接上预期为 0.50.50.5，类似于常数缩放，它阻碍了信号传播。

  如 Fig.2Fig. 2Fig.2 中的灰色箭头所示，快捷连接是信息传递最直接的路径。在快捷连接上的乘法操作（缩放，门控，1×11×11×1 卷积，dropoutdropoutdropout）会阻碍信息传播，导致优化困难。

  值得注意的是，门控和 1×11×11×1 卷积快捷连接会引进更多参数，所以需要比快捷连接有更强的表达能力。事实上，shortcut−onlyshortcut-onlyshortcut−only gatinggatinggating 和 1×11×11×1 卷积覆盖了恒等快捷连接的解空间（即它们可以以恒等快捷连接方式进行优化）。然而，它们的训练误差要高于恒等快捷连接，表明了这些模型的退化问题是由优化问题造成的，而不是表达能力的问题。

  上节的实验验证了 Eqn.(5)Eqn.(5)Eqn.(5) 和 Eqn.(8)Eqn.(8)Eqn.(8) 中的分析，两者都是在基于（附加的激活函数 fff 为恒等映射）这个假设下被推导出的，但是在上述实验中，fff 是 ReLUReLUReLU 函数。因此，Eqn.(5)Eqn.(5)Eqn.(5) 和 Eqn.(8)Eqn.(8)Eqn.(8) 是以上实验的估计，接下来我们研究 fff 的影响。

  我们想要通过重新安排激活函数（ReLUReLUReLU and/orand/orand/or BNBNBN）来使 fff 是一个恒等映射。原始的残差单元的形状如 Fig.4(a)Fig. 4(a)Fig.4(a) 所示 −−--−− 在每个权重层后使用 BNBNBN，并且在 BNBNBN 后使用 ReLUReLUReLU，其中有一个特例：最后一个残差单元的 ReLUReLUReLU 要在逐元素加的后面（即：f=ReLUf = ReLUf=ReLU）。Fig.4(b−e)Fig. 4(b-e)Fig.4(b−e) 展示了我们研究的其他形式，解释如下：

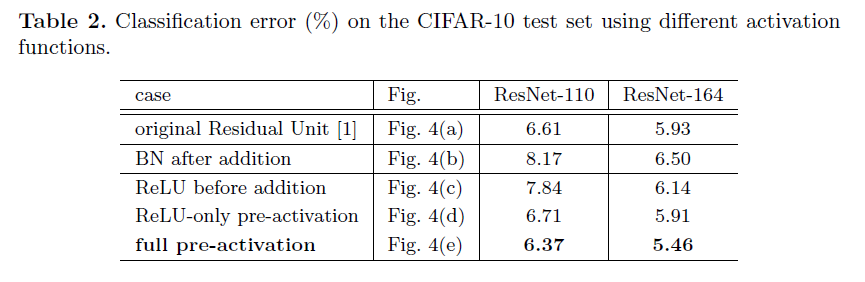
  在该章节中，我们在 ResNet−110ResNet-110ResNet−110 上用一个 164164164 层的瓶颈结构进行实验（称为 ResNet−164ResNet-164ResNet−164）。一个瓶颈残差单元由一个用来降维的 1×1 层、一个 3×3 层、一个用来升维的 1×1 层一起组成的。它的计算机复杂度和两个 3×3 的残差单元很相似，更多细节见附录。ResNet−164ResNet-164ResNet−164 的基本结构在 CIFAR−10CIFAR-10CIFAR−10 上具有良好的结果 5.935.935.93% (Table2)(Table 2)(Table2)。

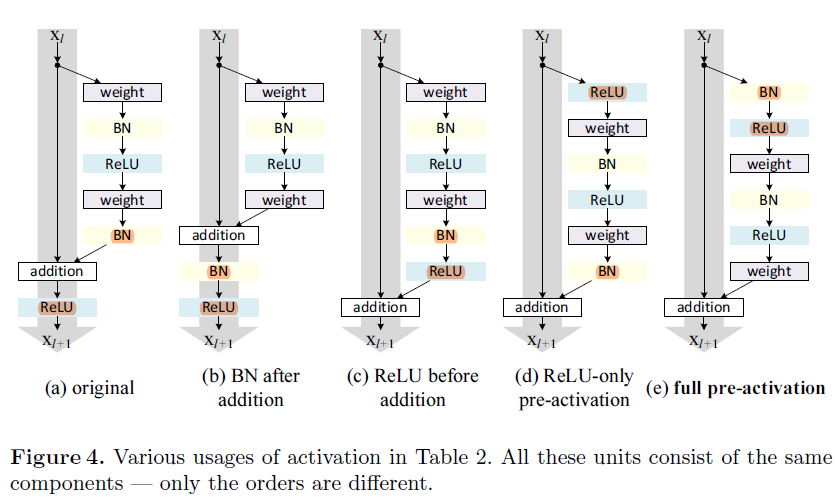
  在将 fff 转化成一个恒等映射之前，我们先采取相反的方法，在逐加法后加一个 BNBNBN (Fig.4(b))(Fig. 4(b))(Fig.4(b))。这种情况下，fff 包含 BNBNBN 和 ReLUReLUReLU。结果变得比基本结构差很多 (Table2)(Table 2)(Table2)。不同于原始的设计，现在的 BNBNBN 层改变了流经快捷连接的信号，阻碍了信号的传播，这从训练一开始，降低训练误差的难度中即可看出 (Fib.6left)(Fib. 6 left)(Fib.6left)。

  使 fff 成为一个恒等映射的最简单的方法就是将 ReLUReLUReLU 移到逐加法之前 (Fig.4(c))(Fig. 4(c))(Fig.4(c))。然而，这导致了变换 FFF 的非负输出，然而一个残差函数的取值应该在 (−∞,∞)(-∞,∞)(−∞,∞)。结果就是，前向传播的信号是单调递增的，这可能会影响表达能力，其结果比基本结构更差了 (7.84(7.84(7.84%, Table2)Table 2)Table2)。我们期望残差函数的值在 (−∞,∞)(-∞,∞)(−∞,∞) 范围内，这个条件可以由包含以下单元的残差单元来实现。

  在原始的设计中 (Eqn.(1)(Eqn.(1)(Eqn.(1) andandand Eqn.(2))Eqn.(2))Eqn.(2))，激活函数 xl+1=f(yl)x_{l+1}=f(y_l)xl+1​=f(yl​) 在两条路径上对下一个残差单元造成影响：yl+1=f(yl)+F(f(yl),Wl+1)y_{l+1}=f(y_l)+F(f(y_l),W_{l+1})yl+1​=f(yl​)+F(f(yl​),Wl+1​)。

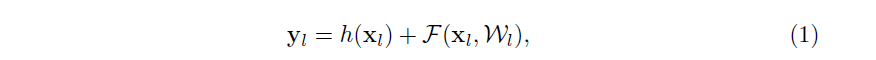
接下来我们开发了一个非对称的形式，其中让激活函数 fff 只对 FFF 路径造成影响：yl+1=yl+F(f(yl),Wl+1)y_{l+1}=y_l+F(f(y_l),W_{l+1})yl+1​=yl​+F(f(yl​),Wl+1​)，对于任意 lll (Fig.5(a)(Fig. 5 (a)(Fig.5(a) tototo (b))(b))(b))。通过对符号重命名，我们可以得到如下形式：


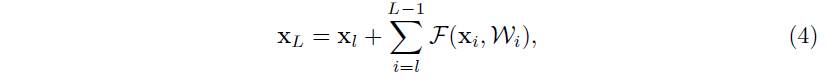
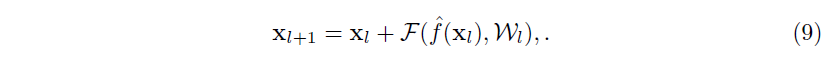
  很容易就可以发现 Eqn.(9)Eqn.(9)Eqn.(9) 与 Eqn.(4)Eqn.(4)Eqn.(4) 很类似，可以使类似于 Eqn.(5)Eqn.(5)Eqn.(5) 的逆向方程成立。对于 Eqn.(9)Eqn.(9)Eqn.(9) 中新的残差单元，新的附加激活函数变成一个恒等映射。这个设计意味着如果一个新的附加激活函数 f^\hat ff^​ 采用非对称，就等同于将 f^\hat ff^​ 重组成下一个残差单元的预激活，如 Fig.5Fig. 5Fig.5 所示

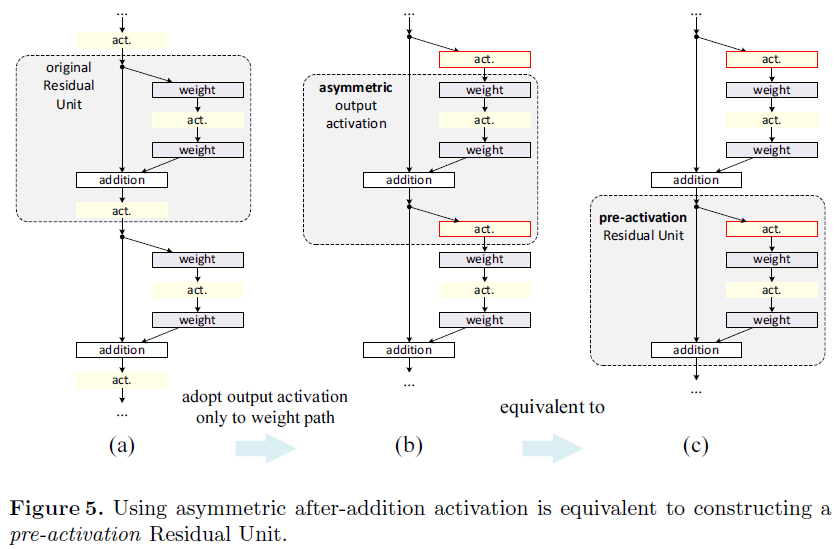
  后激活/预激活的区别是由逐元素加的存在造成的。对于一个有 NNN 层且有 N−1N-1N−1 个激活层（BN/ReLUBN/ReLUBN/ReLU）的普通网络而言，无论我们把其看作是前激活或者后激活都无所谓。但是对于附加的分支层来说，激活函数的位置就变得很重要了。

  我们对以下两种设计进行实验：（i）只用 ReLUReLUReLU 的预激活（ii）全预激活 (Fig.4(e))(Fig. 4(e))(Fig.4(e))，其中 BNBNBN 和 ReLUReLUReLU 都放置在权重层的前面。Table2Table 2Table2 表明仅仅只有 ReLUReLUReLU 的预激活的结果与原始 ResNet−110/164ResNet-110/164ResNet−110/164 类似。ReLUReLUReLU 层不与 BNBNBN 层一起使用，因此无法享受到 BNBNBN 所到来的好处。

  令人惊讶的是，当 ReLUReLUReLU 和 BNBNBN 都在预激活中使用时，结果得到了很可观的提高 (Table2(Table 2(Table2 andandand Table3)Table 3)Table3)。在 Table3Table 3Table3 中记录了使用多种不同体系的结果：（i）ResNet−110ResNet-110ResNet−110（ii）ResNet−164ResNet-164ResNet−164（iii）一个 110110110 层的 ResNetResNetResNet 结构，其中每一个快捷连接仅跳过一层（即一个残差单元仅仅只有一层），表示为 ResNet−110ResNet-110ResNet−110 (1−layer)(1-layer)(1−layer)，以及 (iv)(iv)(iv) 一个有 333333333 个残差单元的 100110011001 层的瓶颈结构（每一个尺寸的 featurefeaturefeature mapmapmap 都有 111111111 个残差单元），表示为 ResNet−1001ResNet-1001ResNet−1001，我们同样在 CIFAR−100CIFAR-100CIFAR−100 上进行实验。Table3Table 3Table3 展示出我们的预激活模型比原始模型的性能要好得多，分析结果如下。

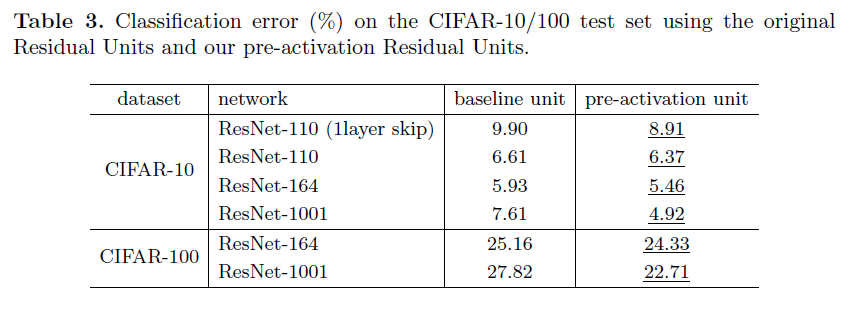
  我们发现预激活的影响具有两个方面。第一，因为 fff 是恒等映射，所以优化更容易（与原始 ResNetResNetResNet 相比）；第二，在预激活中使用 BNBNBN 能提高模型的正则化。

  当训练 100110011001 层 ResNetResNetResNet 时这个影响的效果特别显著（Fig.1Fig. 1Fig.1）。在【1】中使用原始的设计，训练误差在训练初期会下降的很慢。一方面，当 f=ReLUf = ReLUf=ReLU 若为负，那么信号会收到影响，当有很多残差单元时，这个影响会变得尤为突出，Eqn.(3)(Eqn.(3) (Eqn.(3)( 还有 Eqn.(5))Eqn.(5))Eqn.(5)) 并不是一个很好的估计值。另一方面，当 fff 是一个恒等映射时，信号可以在两个单元间直接传播。我们的 100110011001 层网络非常快的减少训练误差。在我们所研究过的所有模型中，它达到了最低的误差，说明优化是成功的。

  我们同样发现了当 ResNetResNetResNet 有很少层时，f=ReLUf = ReLUf=ReLU 的影响并不是很强烈（例如：164164164 层 Fig.6(right)Fig. 6(right)Fig.6(right)）。训练曲线似乎在训练初期受到一点影响，但是马上就会回归到一个良好的状态。通过监控模型的响应，我们发现这是因为在一些训练后，权重会调整值，使得 Eqn.(1)Eqn.(1)Eqn.(1) 中的 yly_lyl​ 总是大于 000，fff 并不会截断它（由于先前 ReLUReLUReLU 的存在，xlx_lxl​ 总是非负的，所以当 FFF 时非负时，yly_lyl​ 就会小于 000）。然而，当使用 100010001000 层模型时，截断就会更加频繁。

  使用预激活单元的另一个影响就是正则化，如 Fig.6(right)Fig.6(right)Fig.6(right) 所示。预激活版在收敛时达到了更高的训练误差，但产生了更少的测试误差。这个现象在 CIFAR−10CIFAR-10CIFAR−10 和 CIFAR−100CIFAR-100CIFAR−100 的数据集上用 ResNet−110ResNet-110ResNet−110，ResNet−110(1−layer)ResNet-110(1-layer)ResNet−110(1−layer) 以及 ResNet−164ResNet-164ResNet−164 上都被观测到。这可能是由 BNBNBN 的正则化效应引起的。在原始残差单元中 (Fig.4(a))(Fig.4(a))(Fig.4(a))，尽管 BNBNBN 使信号归一化，但这很快就被合并到快捷连接上，因此组合的信号并没有被归一化，这个非标准化的信号作为下一个权重层的输入。但恰恰相反，在我们的预激活版本中，所有权重层的输入都是标准化的。

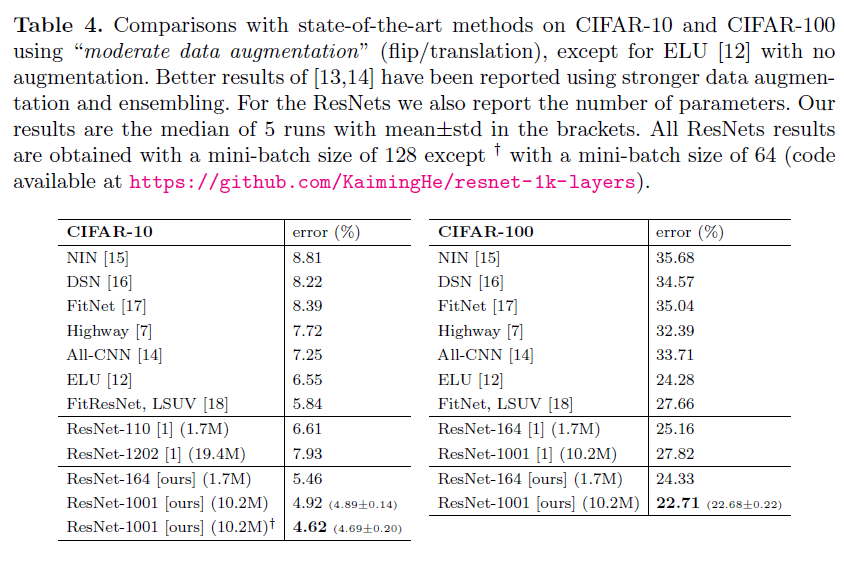
  Table4Table 4Table4 比较了在 CIFAR−10/100CIFAR-10/100CIFAR−10/100 数据集上最先进的方法，我们在其中获得了具有竞争力的结果。我们发现对于小数据集，没有特别地去调整网络的宽度和过滤器大小，也没有使用正则化技术（例如：dropoutdropoutdropout），对其是非常有效的。我们通过一个简单且本质的概念来获得了这些结果。这些结果显示了突破深度极限的潜力。

  接下来，我们展示了在1000类的 ImageNetImageNetImageNet 数据集上的实验结果。我们用 ResNet−101ResNet-101ResNet−101 在 ImageNetImageNetImageNet 数据集上使用跳跃连接做了初步试验，并且观察到类似的优化困难。在初始学习速率下，这些非恒等快捷连接的网络的训练误差显然高于那些原始的 ResNetResNetResNet。并且由于资源有限，我们决定停止训练。但是我们已经用 ResNet−101ResNet-101ResNet−101 在 ImageNetImageNetImageNet 数据集上完成了加法后的 BNBNBN 版本 (Fig.4(b))(Fig. 4(b))(Fig.4(b))，并观察到更高的训练损失和验证误差。这个模型的单裁剪 （224×224）（224×224）（224×224） 验证误差是 24.624.624.6%/7.5/7.5/7.5%，而原始 ResNet−101ResNet-101ResNet−101 的验证误差是 23.623.623.6%/7.1/7.1/7.1%。这和 Fig.6(left)Fig. 6 (left)Fig.6(left) 中 CIFARCIFARCIFAR 的结果一致。

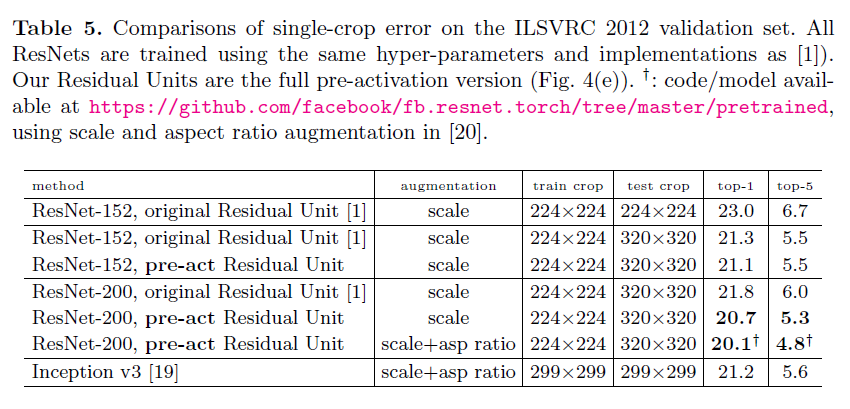
  Table5Table 5Table5 展示了 ResNet−152ResNet-152ResNet−152 和 ResNet−200ResNet-200ResNet−200 的结果，所有训练都从头开始。我们注意到最初的 ResNetResNetResNet 论文【1】使用短边 s∈[256,480]s∈[256,480]s∈[256,480] 的尺寸抖动来训练模型，所以在 s=256s=256s=256 上，224×224224×224224×224裁剪的测试是负偏置的。相反，在所有原始的和我们的 ResNetResNetResNet 上，我们从 s=320s = 320s=320 上裁剪了一个 320×320320×320320×320 的图像进行测试。即使 ResNetsResNetsResNets 在更小的裁剪上进行训练，但他们也可以能够很容易的在更大裁剪上进行测试，因为 ResNetsResNetsResNets 在设计上是全卷积网络，这个尺寸与 InceptionInceptionInception v3v3v3 的 299×299299×299299×299 的尺寸更接近，是一个公平的比较。

  原始的 ResNet−152ResNet-152ResNet−152 在 320×320320×320320×320 的裁切图像上的 top−1top-1top−1 errorerrorerror 为 21.321.321.3%，而预激活版本的 top−1top-1top−1 errorerrorerror 为 21.121.121.1%。在 ResNet−152ResNet-152ResNet−152 上的提升并不大，因为这个模型并没有表现出严重的泛化困难。然而，原始的 ResNet−200ResNet-200ResNet−200 的 top−1top-1top−1 errorerrorerror 为 21.821.821.8%，要高于 ResNet−152ResNet-152ResNet−152 的基本架构。但是我们发现原始 ResNet−200ResNet-200ResNet−200 的训练误差会低于 ResNet−152ResNet-152ResNet−152，表明它受到过拟合的问题。

  我们预激活的 ResNet−200ResNet-200ResNet−200 的错误率为 20.720.720.7%，比 ResNet−200ResNet-200ResNet−200 的基本架构要低1.1%，并且还低于 ResNet−152ResNet-152ResNet−152 的两个版本。当使用尺寸和纵横比增强时，我们的 ResNet−200ResNet-200ResNet−200 的结果要优于 Inceptionv3Inception v3Inceptionv3 的结果 (Table5Table5Table5)。在与我们同期的工作中，Inception−ResNet−v2Inception-ResNet-v2Inception−ResNet−v2 模型的单裁切的结果已经达到了 19.919.919.9%/4.9/4.9/4.9%。我们期望我们的这些观察以及提出的残差单元将会帮助这种类型以及其他类型的 ResNetsResNetsResNets。

  我们模型的计算复杂度和深度呈线性关系（所以一个 100110011001 层网络的复杂度是 100100100 层网络的近 101010 倍）。在 CIFARCIFARCIFAR上，ResNet−1001ResNet-1001ResNet−1001 使用了 222 块 GPUGPUGPU ，花费了 272727 个小时去训练；在 ImageNetImageNetImageNet 上，ResNet−200ResNet-200ResNet−200 使用 888 块 GPUGPUGPU， 花费了将近 333 周的时间去训练(与 VGGVGGVGG 旗鼓相当)。

  本文研究了深度残差网络其连接机制后的传播公式。我们的推导表明，恒等快捷连接和恒等附加激活对信息传播的流畅性是至关重要的。实验证实了与我们的推论一致的现象。我们还提出了可以很容易训练和提高准确率的 100010001000 层深层网络。

identity resnet deep