3D Human Pose Estimation Using Convolutional Neural Networks with 2D Pose Information(2016)
We tackle the 3D human pose estimation task with end-to-end learning using CNNs.Relative 3D positions between one joint and the other joints are learned via CNNs.
两个创新点:(1)we added 2D pose information to estimate a 3D pose from an image by concatenating 2D pose estimation result with the features from an image.
(2)we have found that more accurate 3D poses are obtained by combining information on relative positions with respect to multiple joints,instead of just one root joint.
Introduction
整体介绍Human Pose Estimation——由2D的CNN引入3D的CNN,将CNN的优势扩展到3D——总结【5】【6】【7】CNN网络的缺点,叙述增加2D信息的优势(From 2D pose information,undesirable 3D joint positions which generate unnatural human pose may be discarded)
Frameworkwe propose a simple yet powerful 3D human pose estimation framework based on the regression of joint positions using CNNs.We introduce two strategies to improve the regression results from the baseline CNNs.
(1)not only the image features but also 2D joint classification results are used as input features for 3D pose estimation——this scheme successfully incorporates the correlation between 2D and 3D poses
(2)rather than estimating relative positions with respect to multiple joints——this scheme effectively reduces the error of the joints that are far from the root joint
Related Work
主要介绍基于CNN的2D和3D Human Pose Estimation(详见原文)。
The method proposed in this paper aims to provide an end-to-end learning framework to estimate 3D structure of a human body from a single image.Similar to 【5】,3D and 2D pose information are jointly learned in a single CNN.Unlike the previous works,we directly propagate the 2D classification results to the 3D pose regressors inside the CNNs.
The key idea of our method is to train CNN which performs 3D pose estimation using both image features from the input image and 2D pose information retrieved from the same CNN.In other words,the proposed CNN is trained for both 2D joint clasification and 3D joint regression tasks simultaneously.
Structure of the Baseline CNN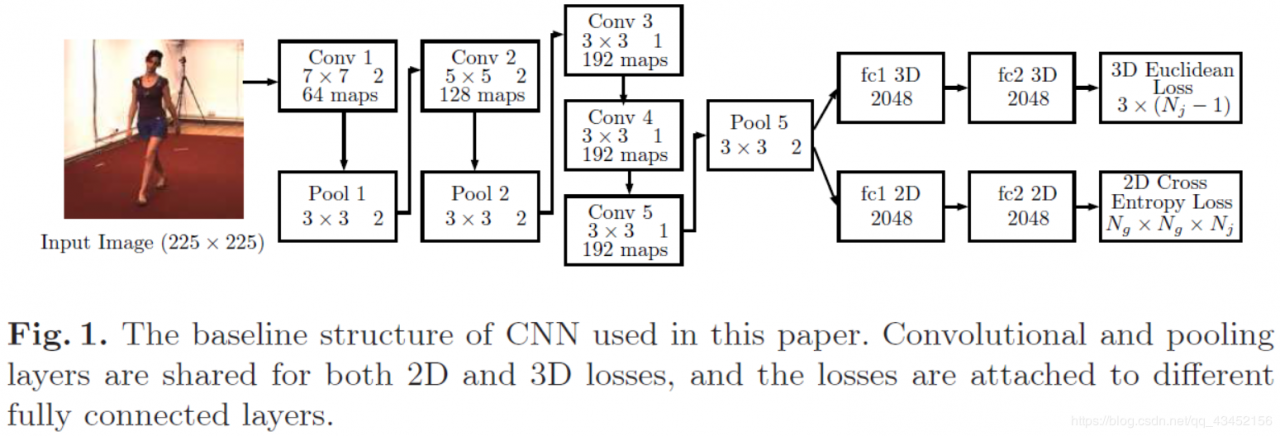
The CNN used in this experiment consists of five convolutional layers, three pooling layers, two parallel sets of two fully connected layers, and loss layers for 2D and 3D pose estimation tasks. The CNN accepts a 225 × 225 sized image as an input. The sizes and the numbers of filters as well as the strides are specified in Figure 1. The filter sizes of convolutional and pooling layers are the same as those of ZFnet 【21】, but we reduced the number of feature maps to make the network smaller.
We divided an input image into Ng×NgN_g×N_gNg×Nggrids and treat each grid as a separate class,which results in Ng2N_g^2Ng2classes per joint.The target probability fot the ithithith grid gig_igi of the jthjthjth joint is inversely proportional to the distance from the ground truth position.
p^j(gi)=d−1(y^j,ci)I(gi)∑k=1Ng2d−1(y^j,ck)I(gk) (1)\hat p_j(g_i)=\frac{d^{-1}(\hat y_j,c_i)I(g_i)}{\sum _{k=1}^{N_g^2}d^{-1}(\hat y_j,c_k)I(g_k)}\space (1)p^j(gi)=∑k=1Ng2d−1(y^j,ck)I(gk)d−1(y^j,ci)I(gi) (1)
——d−1(x,y)d^{-1}(x,y)d−1(x,y) is the inverse of the Euclidean distance between the point x and y in the 2D pixel space,y^j\hat y_jy^j is the ground truth position of the jthjthjth joint in the image,and cic_ici is the center of the grid gig_igi.
I(gi)I(g_i)I(gi) is an indicator function that is equal to 1 if the grid gig_igi is one of the four nearest neighbors.
I(gi)={1 ifd(y^j,ci)<ωgo otherwise,(2)I(g_i)=
\begin {cases}
1\space \space if d(\hat y_j,c_i)<\omega_g\\
o\space \space otherwise,
\end {cases}
(2)I(gi)={1 ifd(y^j,ci)<ωgo otherwise,(2)
——ωg\omega_gωg is the width.Hence,higher probability is assigned to the grid closer to the ground truth joint positon,and p^j(gi)\hat p_j(g_i)p^j(gi) is normalized so that the sum og the class probabilities is equal to 1.Finally,the objective of the 2D classification task for the jthjthjth join is to minimize the following cross entropy loss function.
L2D(j)=−∑i=1Ng2p^j(gi)logpj(gi), (3)L_{2D}(j)=-\sum_{i=1}^{N_g^2}\hat p_j(g_i)logp_j(g_i),\space (3)L2D(j)=−i=1∑Ng2p^j(gi)logpj(gi), (3)
——pj(gi)p_j(g_i)pj(gi) is the probability that comes from the softmax output of the CNN.
Estimating 3D position of joints is formulated as a regression task.Since the search space is much larger than the 2D case,it is undersirable to solve 3D pose estimation as a classification task.The 3D loss funcion is designed as a square of the Euclidean distance between the prediction and the ground truth.We estimate 3D position of each joint relative to the root node.the loss function for the jthjthjth joint when the root node is the rthrthrth joint becomes
L3D(j,r)=∣∣Rj−(J^j−J^r)∣∣2 (4)L_{3D}(j,r)=||R_j-(\hat J_j - \hat J_r)||^2\space (4)L3D(j,r)=∣∣Rj−(J^j−J^r)∣∣2 (4)
——RjR_jRj is the predicted relative 3D position of the jthjthjth joint from the root node,J^j\hat J_jJ^j is the ground truth 3D position of the jthjthjth joint,and J^r\hat J_rJ^r is that of the root node.The overall cost function of the CNN combines (3) and (4) with weights,
Lall=λ2D∑j=1NjL2D(j)+λ3D∑j≠rNjL3D(j,r) (5)L_{all}=\lambda_{2D}\sum _{j=1}^{N_j}L_{2D}(j)+\lambda_{3D}\sum_{j≠r}^{N_j}L_{3D}(j,r)\space (5) Lall=λ2Dj=1∑NjL2D(j)+λ3Dj=r∑NjL3D(j,r) (5)
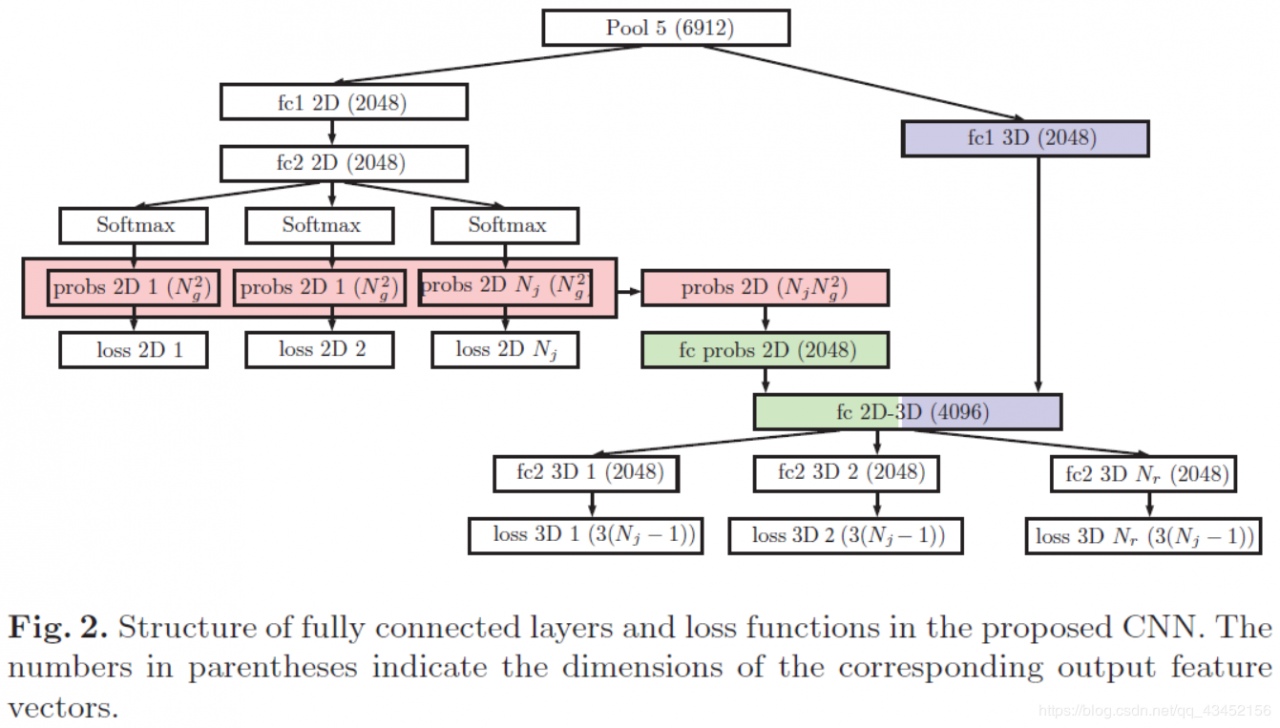
详见原文。The joint locations in an image are usually a strong cue of guessing 3D pose.To exploit 2D classification result for the 3D pose estimation,we concatenate the outputs of softmax in the 2D classification task with the outputs of the fully connected layers in the 3D loss part.The proposed structure after the last pooling layer is shown in Figure(2).First,the 2D classification result is concatenated(probs 2D layer in Figure2probs\space 2D \space layer \space in \space Figure2probs 2D layer in Figure2)and passes the fully connected layer(fc probs 2Dfc\space probs\space 2Dfc probs 2D).Then,the feature vectors from 2D and 3D part are concatenated(fc 2D−3Dfc\space 2D-3Dfc 2D−3D),which is used for 3D pose estimation task.Note that the error from the fc probs 2D layer is not back-propagated to the probs 2D layer to ensure that layers used for the 2D classification are trained only by the 2D loss part.【3】repeatedly uses the 2D classification result as an input by concatenating it with feature maps from CNN.we simply vectorized the softmax result to produce Ng×Ng×NjN_g×N_g×N_jNg×Ng×Nj feature vector rather than convolving the probability map with features in the convolutional layers.

介绍基础框架及其缺点,【5】提出一种解决办法,并介绍了【5】的缺点,进而提出本文的方法:we estimate the relative position over multiple joints.(基础框架计算各关节与根关节的相对位置,缺点是距离越远,精度越低。【5】提出计算各个节点与父节点之间的相对位置,缺点是中间节点的误差会累积)。令NrN_rNr为选择的根节点的数目。实验中令Nr=6N_r=6Nr=6可以使得大部分关节或者是根节点或者是邻居节点,可视化如图3(b)。6个3D regression losses如图2。整体误差为
Lall=λ2D∑j=1NjL2D(j)+λ3D∑r∈R∑j≠rNjL3D(j,r) (6)L_all=\lambda_{2D}\sum_{j=1}^{N_j}L_{2D}(j)+\lambda_{3D}\sum_{r\in R}\sum_{j≠r}^{N_j}L_{3D}(j,r)\space (6)Lall=λ2Dj=1∑NjL2D(j)+λ3Dr∈R∑j=r∑NjL3D(j,r) (6)
——RRR is the set containing the joint indices that are used as root nodes.When the 3D losses share the same fully connected layers,the trained model outputs the same pose estimation results across all joints.To break this symmetry,we put the fully connected layers for each 3D losses(fc2 layers in Figure2fc2\space layers\space in\space Figure2fc2 layers in Figure2)
At the test time,all the pose estimation results are translated so that the mean of each pose bacomes zero.Final prediction is generated by averaging the translated results.In other words,the 3D position of the jthjthjth joint XjX_jXj is calculated as
Xj=∑r∈RXj(r)Nr (7)X_j=\frac{\sum _{r\in R}X_j^{(r)}}{N_r}\space (7)Xj=Nr∑r∈RXj(r) (7)
——Xj(r)X_j^{(r)}Xj(r) is the predicted 3D position of the jthjthjth joint when the rthrthrth joint is set to a root node.
详见原文
ConclusionsWe expect that the perfprmance can be further improved by incorporating temporal information to the CNN by applying the concepts of recurrent neural network or 3D convolution[26].Also,efficient aligning method for multiple regression results may boost the accuracy of pose estimation.
作者:qq_43452156