汉诺塔代码图文详解(递归入门)
游戏规则:
| 已知条件 | 存在A,B,C三根柱子,A上套有N片圆盘 (如下图) |
|---|---|
| 目的 | 将A上的所有圆盘移到C上 |
| 约束条件 | 每次只能移动一片圆盘,且整个过程中只能出现小圆盘在大圆盘之上的情况 |

首先我们模拟(N=2,3,4).
这是两层汉诺塔的移动步骤.
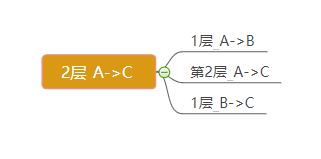
这是三层汉诺塔的步骤.
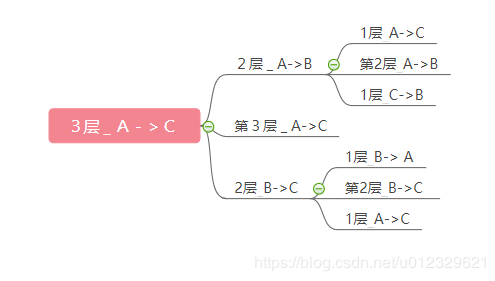
这是四层的汉诺塔步骤.
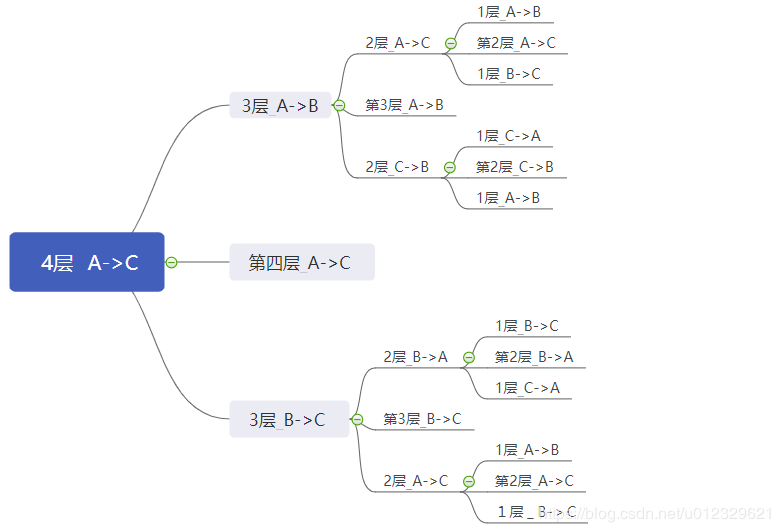
移动规律:做完模拟之后可以很自然地发现,要把N层的汉诺塔从A柱移至C柱,首先是要把上面(N-1)片圆盘全部拿掉(也就是移至B处),然后才能把 第 N片圆盘移至C柱.
当我们成功地把第N片圆盘移至C柱时,问题转化成了要把B柱上的(N-1)片圆盘移至C处.然后重复上述操作:把(N-2)片圆盘全部移至A柱,再把 第 (N-1)片圆盘移至C柱…
思路分析:从移动规律上看,我们是把要移动的n片圆盘分成两个整体:(n-1)片和第n片,那么这两个整体可以看作是N=2的汉诺塔问题的部分解.
关于移动次数的分析:观察上述过程图,发现中间部分的关于"n-1"层的移动实际上是不进行的,它其实是我们分析问题的中间假象项,它由下一层递归去实现,而下一层的"n-1"层的移动又是由下一层递归去实现,最后递归到"n-1"=1时,这一次的"n-1"项才真正开始移动.那么,每下一次递归的关于"n-1"层的移动项是这一次关于"n-1"的移动项的2倍.所以当n-1次递归后,最后会造就 2^(n-1) ①次数的"n-1"=1的移动…
而关于第n层移动的项每次递归都会执行一次.那么关于第n层移动的次数是20 + 21 +22 +23 +…+ 2n-2 ②;
综合①②得Sn=20 + 21 +22 +23 +…+ 2n-2+2n-1 ;
Sn是关于a1=1,an=2n-1的等比数列.
计算得Sn=2n -1
[结合上述内容其实不难发现,我们可以用递归的思想去实现代码]
如果还不是很清楚,我们不妨先打下代码的大致框架,随后逐步完善。。。
//代码框架
#include
void Move()
{
}
void HannuoTower()
{
}
int main()
{
int N;
scanf("%d",&N);
HannuoTower();
}
由模拟(N=2,3,4)的过程图得知,HannuoTower函数分为三个步骤:
(A柱B柱C柱视不同情况而分为:圆盘当前所在位置,要移动的目标位置,临时存放的第三位置)
1.先移动(n-1)片圆盘到第三位置 //(无法一次性实现)这个步骤的实现用递归
2.再移动 第 n片圆盘到目标位置 //Move函数直接移动输出
3.最后移动(n-1)片圆盘到 第 n片圆盘之上(也就是目标位置) //实现方法同步骤1.
于是乎,HannuoTower函数和Move可以写成如下形式
void Move(char a,char c)
{
printf("%c -> %c",a,c);
}
void HannuoTower(void n,char a,char b,char c)//n为层数
//固定地将形参a视为当前位置,形参b视为临时位置,形参c视为目标位置.
{
HannuoTower(n-1,a,c,b); //较下一次情况,临时位置和目标位置的身份互换
Move(a,c);//输出 当前位置移至目标位置的信息
HannuoTower(n-1,b,a,c);//较下一次情况,当前位置和临时位置的身份互换
}
这里要注意一点的是,此时的HannuoTower函数是无法作用的,当n减到1时,它还是会递归下去.递归函数最重要的是设置出口,这里我们可以用if语句去判断跳出的条件(n==1).
此外,为了方便观察汉诺塔游戏的过程和研究圆盘移动次数的计算规律.我们可以另加一个全局变量count,用来计数移动的次数.
补充完整的代码如下.
#include
int count=1;
void Move(char a,char c)
{
printf("第%d次,%c -> %c\n",count,a,c);
count++;
}
void HannuoTower(int n,char a,char b,char c)
{
if(n==1)Move(a,c);
else
{
HannuoTower(n-1,a,c,b);
Move(a,c);
HannuoTower(n-1,b,a,c);
}
}
int main()
{
int n;
scanf("%d",&n);
HannuoTower(n,'A','B','C');
}
作者:1336168684