二叉树的遍历与哈夫曼树的构造详解
递归式:根结点->左子树->右子树
递归边界 :二叉树是一棵空树
void preorder(node* root){
if(root==NULL){
return;//到达空树,递归边界
}
//访问根结点root,例如将其数据域输出
printf("%d\n",root->data);
//访问左子树
preorder(root->lchild);
//访问右子树
preorder(root->rchild);
}
2、二叉树的中序遍历
算法思想
递归式: 中序遍历左子树->访问根结点->中序遍历右子树
递归边界: 二叉树是一棵空树
void inorder(node* root) {
if(root==NULL){
return;//递归出口
}
//访问左子树
inorder(root->lchild);
//访问根结点root,例如将其数据域输出
printf("%d\n",root->data);
//访问右子树
inorder(root->rchild);
}
3、二叉树的后序遍历
算法思想
递归式: 后序遍历左子树->后序遍历右子树->访问根结点。
递归边界: 二叉树是一棵空树
void postorder(node* root){
if(root==NULL){
return ;//递归出口
}
//访问左子树
postorder(root->lchild);
//访问右子树
postorder(root->rchild);
//访问根结点
printf("%d\n",root->data);
}
4、二叉树的层序遍历
算法思想
按层次的顺序从根结点向下逐层进行遍历,且对同一层的节点为从左到右进行遍历。与BFS相似,需要用到队列。
算法步骤实现步骤:
1.将根节点root加入队列q
2.取出队首结点,访问它
3.如果该结点有左孩子,将其入队
4.如果该结点有右孩子,将其入队
5.返回2.直到队列为空
void LayerOrder(node* root){
queueq;
q.push(root);
while(!q.empty()){
node* now=q.front();
q.pop();
printf("%d",now->data);
if(now->lchild!=NULL) {
q.push(now->lchild);
}
if(now->rchild!=NULL){
q.push(now->lchild);
}
}
}
(二)二叉树遍历相关试题分析
1、已知中序后序求层序
试题描述
给出一颗二叉树的后序遍历序列和中序遍历序列,求这颗二叉树的层序遍历序列 。
输入样例7
2 3 1 5 7 6 4
1 2 3 4 5 6 7
4 1 6 3 5 7 2
算法分析已知中序后序可以唯一确定一个二叉树,所以先构造二叉树再进行遍历。
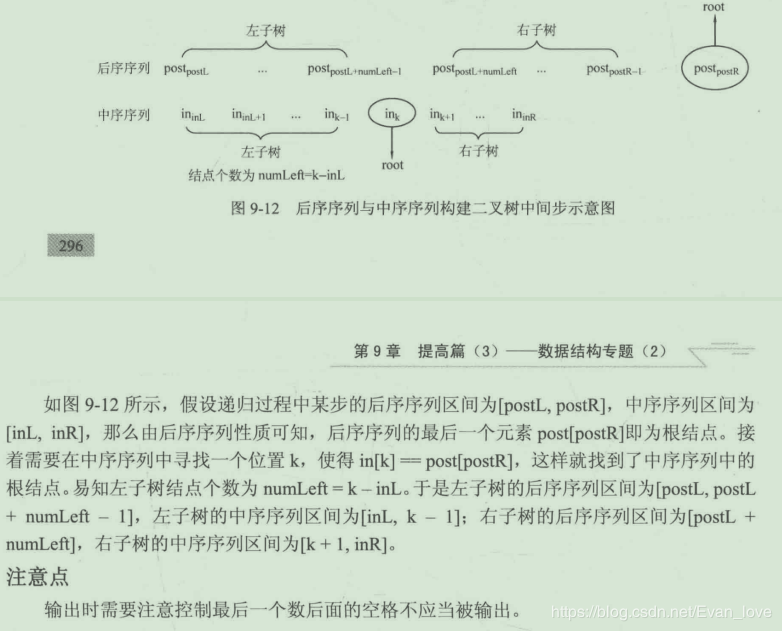 代码
代码
#include
#include
#include
#include
#include
#include
#include
using namespace std;
const int maxn=50;
struct node{
int data;
node* lchild;
node* rchild;
};
int pre[maxn],in[maxn],post[maxn];//先序、中序、后序
int n;//结点个数
//当前二叉树的后序序列区间为[postL,postR]
//中序序列区间为[inL,intR]
//create函数返回构建出的二叉树根结点地址
node* create(int postL,int postR,int inL,int inR){
if(postL>postR){
return NULL;//后序序列长度小于等于0时,直接返回
}
node* root=new node;//新建一个新的结点,用来存放当前二叉树的根结点
root->data=post[postR];//新结点的数据域为根结点的值
int k;
for(k=inL;klchild=create(postL,postL+numLeft-1,inL,k-1);
//返回右子树的根结点地址,赋值给root的指针
root->rchild=create(postL+numLeft,postR-1,k+1,inR);
return root;//返回根结点地址
}
int num=0;//已输出的结点个数
void layerOrder(node* root){
queue q;//注意队列中存的为地址
q.push(root);
while(!q.empty()) {
node* now=q.front();//取出队首元素
q.pop();
printf("%d",now->data);
num++;
if(numlchild!=NULL){
q.push(now->lchild);
}
if(now->rchild!=NULL){
q.push(now->rchild);
}
}
}
int main(int argc, char** argv) {
scanf("%d",&n);
for(int i=0;i<n;i++){
scanf("%d",&post[i]);
}
for(int i=0;i<n;i++){
scanf("%d",&in[i]);
}
node* root=create(0,n-1,0,n-1);//建树
layerOrder(root); //层序遍历
return 0;
}
2、已知先序中序求后序
试题描述
已知某二叉树的先序序列和中序序列,编程计算并输出该二叉树的后序序列
输入说明仅一组数据,分为两行输入,第一行表示指定二叉树的先序序列,
第二行表示该二叉树的中序序列,序列元素均为大写英文字母,表示二叉树的结点
一行上输出该二叉树的后序序列
输入样例ABDGCEFH
DGBAECHF
GDBEHFCA
算法分析需要使用先序后序构造一颗二叉树再遍历。
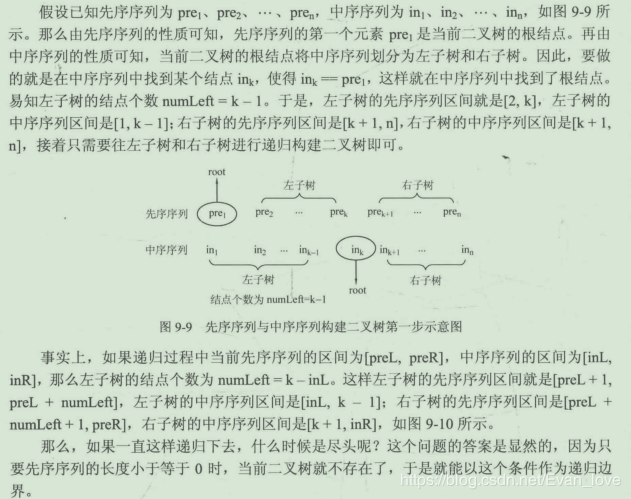
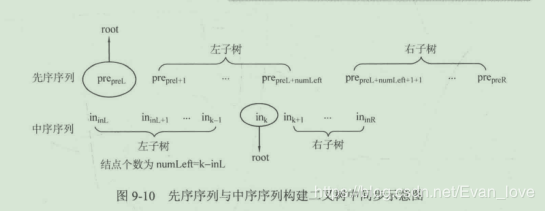 代码
代码
#include
#include
#include
using namespace std;
struct Node
{
char data;
Node * lchild;
Node * rchild;
};
Node* CreatTree(string pre, string in)
{
Node * root = NULL; //树的初始化
if(pre.length() > 0)
{
root = new Node; //为根结点申请结构体所需要的内存
root->data = pre[0]; //先序序列的第一个元素为根结点
int index = in.find(root->data); //查找中序序列中的根结点位置
//substr(a,b),从第a个下标的元素开始截取b个元素
//所需的子字符串的起始位置。字符串中第一个字符的索引为 0,默认值为0
/**
stringObject.substr(start,length);
start--必需。要抽取的子串的起始下标。必须是数值。若为负数,那么该参数声明从字符串的尾部开始算起的位置
length--可选。字串中的字符数。必需是数值。如果省略了该参数,那么返回从stringObject开始到结尾的字符串
*/
root->lchild = CreatTree(pre.substr(1, index), in.substr(0, index)); //递归创建左子树
root->rchild = CreatTree(pre.substr(index + 1), in.substr(index + 1)); //递归创建右子树
}
return root;
}
void PostOrder(Node * root) //递归后序遍历
{
if(root != NULL)
{
PostOrder(root->lchild);
PostOrder(root->rchild);
cout<data;
}
}
int main()
{
string pre_str, in_str;
Node *root;
while(cin>>pre_str>>in_str)
{
root = CreatTree(pre_str, in_str);
PostOrder(root);
cout<<endl;
}
return 0;
}
(三)哈夫曼树基础
1、哈夫曼树的特点
(1)每个初始结点最终都成为叶结点,并且权值越小的结点到根结点的路径长度越大
(2)构造过程中共新建了N-1个结点(双分支结点),因此哈夫曼树中结点总数为2N-1
(3)每次构造都选择2颗树作为新结点的孩子,因此哈夫曼树中不存在度为1的结点
给定N个权值分别为w1,w2,w3,…,wn的结点。通过哈夫曼算法可以构造出最优二叉树,算法描述如下:
(1)将这N个节点跟别作为N棵仅含一个结点的二叉树,构成森林F
(2)构造一个新结点,并从F中选取两颗根结点权值最小的树作为新结点的左右子树,并且将新结点的权值置为左右子树上根节点的权值之和
(3)从F中删除刚才选出的两颗树,同时将新得到的树加入到F中
(4)重复步骤(2),(3)直至F中只剩下一棵树为止。
WPL = 所有叶子结点的带权路径长度之和
4、哈弗曼编码1.对于任何一个叶子结点,其编号一定不会成为其他任何一个结点编号的前缀。
(四)、哈夫曼树相关例题分析 1、西电考研2011年机试试题Problem D 试题描述假设用于通信的电文由n(4<n<30)个字符组成,字符在电文中出现的频度(权值)为w1,
w2,wn,试根据该权值构成哈夫曼树,并计算该数的带权路径长度。
仅一组数据。分为两行输入:第一行为n的值,第二行为n个整数,表示字符出现的频度
输出说明一个整数,表示所构造的哈夫曼树的带权路径长度
输入样例8
7 19 2 6 32 3 21 10
261
试题分析该题需要使用优先级队列实现,由算法思想和步骤来定义优先级规则,然后需要使用小顶堆实现。每次从待取结点中挑出最小的两个。 代码
#include
#include
#include
#include
using namespace std;
int main(){
int n;
cin>>n;
long long w,front1,front2,sum=0,wpl=0;
//使用优先级队列进行处理,小顶堆实现
priority_queue<long long,vector,greater > q;
for(int i=0;i>w;
q.push(w);
}
while(q.size()>1){
front1 = q.top();
q.pop();
front2=q.top();
q.pop();
sum=front1+front2;
wpl+=sum;
q.push(sum);
}
cout<<wpl<<endl;
return 0;
}
(五)参考文献
【1】2018年数据结构考研复习指导. 王道论坛编.
【2】算法笔记. 胡凡,曾磊 主编.
【3】2020年攻读硕士学位研究生复试资料.
作者:Evan_love