数学知识——概率统计（10）：分布和小结

学的有些模糊了，回过头来突然想不起“概率”到底是什么定义，也不知道“分布”的含义，还有，概率统计到底在干一件什么事情？

跳出细枝末节，宏观的来看，其实，本质上不也就是在玩“数据”么：

数据——随机变量；
获取数据——抽样；
描述数据——分布（总体的细节描述）、统计量（总体的概述）、相关性分析（变量之间）；
分析数据——统计推断方法（参数估计、假设检验）；
规律描述——大数定理、中心极限定理
…

注：分析分布（而不是分析有限的样本）需要使用CDF。

分布
描述变量的最佳方法之一是列出该变量在数据集中的值，以及每个值出现的次数。这种描述称为该变量的分布（distribution）。

分布最常用的呈现方法是直方图（histogram），即展示每个值的频数（frequency）的图形。在这里，“频数”指一个值出现的次数。
ps：直方图是一个样本分布的完整描述，也可以使用几个描述性的统计量对变量进行一个概述。

除了直方图，另一种可以表示分布的方法是概率质量函数（probability mass function，PMF）。概率质量函数将每个值映射到其概率。
ps：概率（probability）是频数的分数表示，样本量为n。要从频数计算出概率，我们将频数除以n，这一过程称为正态化（normalization）。

直方图和PMF的区别：直方图将值映射到整数型的计数值，而PMF将值映射到浮点型的概率值。

累积分布函数（CDF）
CDF（cumulative distribution function）

PMF适用于变量值数量较少的情况。
在进行分布比较时，CDF尤为有用。

概率密度函数（PDF）
CDF的导数称为概率密度函数（probability density function，PDF）。
对于特定值x，人们通常不会计算其PDF。计算PDF得到的不是概率，而是概率密度（density）。

在物理学上，密度是单位体积的质量。要计算质量，必须用密度乘以体积。如果密度不是常量，那么需要将其与体积进行积分。
类似地，概率密度度量单位 x 的概率。为了计算概率，必须在 x 的取值范围上进行积分。
（x是变量了，需要积分了）

核密度估计（kernel density estimation，KDE）是一种算法，可以对一个样本寻找符合样本数据的适当平滑的PDF。

分布框架

分布函数的关系框架：

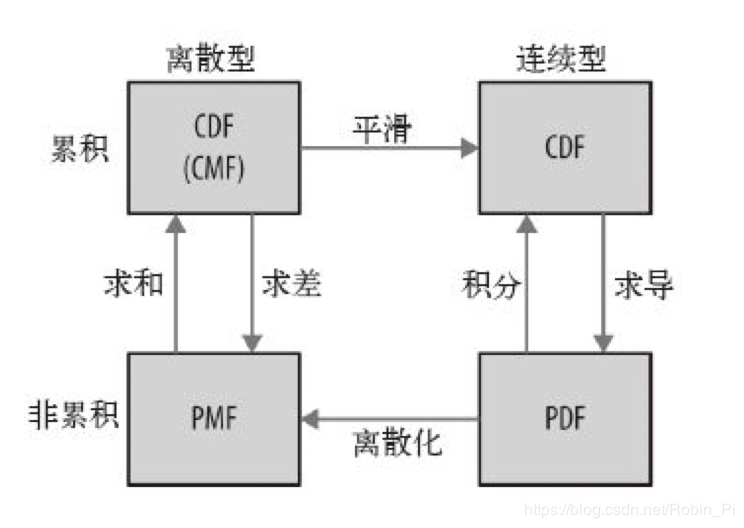
我们最先接触的是PMF。PMF代表一组离散值的概率。要从PMF得到CDF，需要把概率值累加得到累积概率。反过来，要从CDF得到PMF，需要计算累积概率之间的差值。我们将在接下来的几节讨论这些计算的具体实现。

PDF是连续型CDF的导数，或者说，CDF是PDF的积分。请记住：PDF将值映射到概率密度，要得到概率，必须进行积分运算。

要从离散型分布得到连续型分布，可以进行各种平滑处理。一种平滑处理方法是，假设数据来自一个连续的分析分布（如指数分布或正态分布），然后估计这个分布的参数。另一种方法是核密度估计。

平滑处理的逆向操作是离散化（discretizing），或称为量化（quantizing）。如果在离散点上计算PDF，就可以生成近似这个PDF的PMF。使用数值积分可以获得更好的近似。

参考：

小结 概率统计 分布 数学