【赛后诸葛】2020 力扣杯!Code Your Future 春季全国编程大赛
第一次参加leetcode的比赛,比赛结果比较惨淡。AC两道,然后就陷入了超时的困境。记录一下这次比赛的题目以及解题方案吧,至于没有过的题目,当然是赛后诸葛了~
桌上有 n 堆力扣币,每堆的数量保存在数组 coins 中。我们每次可以选择任意一堆,拿走其中的一枚或者两枚,求拿完所有力扣币的最少次数。
示例 1:
输入:[4,2,1]
输出:4
解释:第一堆力扣币最少需要拿 2 次,第二堆最少需要拿 1 次,第三堆最少需要拿 1 次,总共 4 次即可拿完。
示例 2:
输入:[2,3,10]
输出:8
限制:
1 <= n <= 4
1 <= coins[i] <= 10
解题思路
思路比较清晰,遍历数组vector,每次一次最多拿两个,直到拿完为止。这里有一个小技巧,就是把每个数字加1再除以二刚好满足我们的需求。
AC代码
class Solution {
public:
int minCount(vector& coins) {
int res = 0;
for(auto c : coins) res += (c+1)/2;
return res;
}
};
2. 传递信息
小朋友 A 在和 ta 的小伙伴们玩传信息游戏,游戏规则如下:
有 n 名玩家,所有玩家编号分别为 0 ~ n-1,其中小朋友 A 的编号为 0 每个玩家都有固定的若干个可传信息的其他玩家(也可能没有)。传信息的关系是单向的(比如 A 可以向 B 传信息,但 B 不能向 A传信息)。 每轮信息必须需要传递给另一个人,且信息可重复经过同一个人给定总玩家数 n,以及按 [玩家编号,对应可传递玩家编号] 关系组成的二维数组 relation。返回信息从小 A (编号 0 ) 经过 k 轮传递到编号为 n-1 的小伙伴处的方案数;若不能到达,返回 0。
示例 1:
输入:n = 5, relation = [[0,2],[2,1],[3,4],[2,3],[1,4],[2,0],[0,4]], k = 3
输出:3
解释:信息从小 A 编号 0 处开始,经 3 轮传递,到达编号 4。共有 3 种方案,分别是 0->2->0->4, 0->2->1->4, 0->2->3->4。
示例 2:
输入:n = 3, relation = [[0,2],[2,1]], k = 2
输出:0
解释:信息不能从小 A 处经过 2 轮传递到编号 2
限制:
2 <= n <= 10
1 <= k <= 5
1 <= relation.length <= 90, 且 relation[i].length == 2
0 <= relation[i][0],relation[i][1] < n 且 relation[i][0] != relation[i][1]
解题思路
做题时的解题思路是打印出k轮传递全部的可能性路线,然后终点为n-1时路线+1;
但作为赛后诸葛,当然是推荐动态规划解题法。
利用二维数组dp[i][j]的值记录从玩家0开始经过i轮可以到达的玩家j的次数。
所以根据题意,i的最大值为6,j的最大值为10;
定义:dp[6][10];
初始化:memset(dp,0,sizeof(dp)); dp[0][0] = 1;
状态转移方程:dp[i][r[1]] += dp[i - 1][r[0]]
状态转移理解:r[0]->r[1] 表示传递路线
意思就是目前这一轮的状态是由前一轮状态遍历循环再传递一次得到的。
拿示例 1举例:(因为k = 3, n = 5,所以下面的二维数组简化了)
初始状态为:(从0出发)
1 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
经过一轮传递后状态为:(因为从初始化状态(玩家0)出发,只传递一轮只会到达2或4一次)
0->2
0->4
1 0 0 0 0
0 0 1 0 1
0 0 0 0 0
0 0 0 0 0
经过第二轮传递后状态为:(因为第一轮后的状态(玩家2或玩家4各一次)出发,再次传递一轮会到达玩家0,1,3各一次)
2->1
2->3
2->0
1 0 0 0 0
0 0 1 0 1
1 1 0 1 0
0 0 0 0 0
经过第三轮传递后状态为:(因为第二轮后的状态(0,1,3各一次)出发,再次传递一轮会到达玩家2一次,玩家4三次)
0->2
3->4
1->4
0->4
1 0 0 0 0
0 0 1 0 1
1 1 0 1 0
0 0 1 0 3
所以这个二维数组意思也非常清楚,通过遍历路线,累加二维数组的值。二维数组的第一个维度表示传递的次数,第二个维度表示传递的路线。
AC代码
class Solution {
public:
int numWays(int n, vector<vector>& relation, int k) {
int dp[6][10];
memset(dp,0,sizeof(dp));
dp[0][0] = 1;
for(int i = 1; i <= k; i += 1) {
for(auto r : relation) {
dp[i][r[1]] += dp[i - 1][r[0]];
}
}
return dp[k][n - 1];
}
};
3. 剧情触发时间
在战略游戏中,玩家往往需要发展自己的势力来触发各种新的剧情。一个势力的主要属性有三种,分别是文明等级(C),资源储备(R)以及人口数量(H)。在游戏开始时(第 0 天),三种属性的值均为 0。
随着游戏进程的进行,每一天玩家的三种属性都会对应增加,我们用一个二维数组 increase 来表示每天的增加情况。这个二维数组的每个元素是一个长度为 3 的一维数组,例如 [[1,2,1],[3,4,2]] 表示第一天三种属性分别增加 1,2,1 而第二天分别增加 3,4,2。
所有剧情的触发条件也用一个二维数组 requirements 表示。这个二维数组的每个元素是一个长度为 3 的一维数组,对于某个剧情的触发条件 c[i], r[i], h[i],如果当前 C >= c[i] 且 R >= r[i] 且 H >= h[i] ,则剧情会被触发。
根据所给信息,请计算每个剧情的触发时间,并以一个数组返回。如果某个剧情不会被触发,则该剧情对应的触发时间为 -1 。
示例 1:
输入: increase = [[2,8,4],[2,5,0],[10,9,8]] requirements = [[2,11,3],[15,10,7],[9,17,12],[8,1,14]]
输出: [2,-1,3,-1]
解释:
初始时,C = 0,R = 0,H = 0
第 1 天,C = 2,R = 8,H = 4
第 2 天,C = 4,R = 13,H = 4,此时触发剧情 0
第 3 天,C = 14,R = 22,H = 12,此时触发剧情 2
剧情 1 和 3 无法触发。
示例 2:
输入: increase = [[0,4,5],[4,8,8],[8,6,1],[10,10,0]] requirements = [[12,11,16],[20,2,6],[9,2,6],[10,18,3],[8,14,9]]
输出: [-1,4,3,3,3]
示例 3:
输入: increase = [[1,1,1]] requirements = [[0,0,0]]
输出: [0]
限制:
1 <= increase.length <= 10000
1 <= requirements.length <= 100000
0 <= increase[i] <= 10
0 <= requirements[i] <= 100000
解题思路
这道题的思路比较清楚,就是通过每天的属性值,然后对比是否达到剧情触发条件。但是困难的地方在于如果只是简单的暴力解答会导致超时。这里需要注意的是,当数组遍历超时且数组每个序列都需要访问时,可以通过排序数组的二分查找缩短时间。
然后看这道题,如果对剧情排序的话,还需要考虑剧情本身就是有顺序要求的。而比较观察的是,虽然每天增加的属性值也不是排序数组,但是玩家的每天属性值天然就是个排序数组,这样的话,我们可以通过把玩家每天的属性值记录下来,然后遍历剧情数组,对玩家每天的属性值进行二分查找即可达到要求。
AC代码
class Solution {
public:
vector getTriggerTime(vector<vector>& increase, vector<vector>& requirements) {
vector player = {0,0,0};
vector res(requirements.size(), -1);
vector<vector> days = {player};
//记录每天玩家的属性值
for(int i = 0; i < increase.size(); i++) {
player[0] += increase[i][0];
player[1] += increase[i][1];
player[2] += increase[i][2];
days.push_back(player);
}
for(int i = 0; i days[right][0] || requirements[i][1] > days[right][1] || requirements[i][2] > days[right][2]) continue;
//二分查找并赋值
while(left = requirements[i][0] && days[middle][1] >= requirements[i][1] && days[middle][2] >= requirements[i][2]) {
right = middle - 1;
}else {
left = middle + 1;
}
}
res[i] = left;
}
return res;
}
};
4. 最小跳跃次数
为了给刷题的同学一些奖励,力扣团队引入了一个弹簧游戏机。游戏机由 N 个特殊弹簧排成一排,编号为 0 到 N-1。初始有一个小球在编号 0 的弹簧处。若小球在编号为 i 的弹簧处,通过按动弹簧,可以选择把小球向右弹射 jump[i] 的距离,或者向左弹射到任意左侧弹簧的位置。也就是说,在编号为 i 弹簧处按动弹簧,小球可以弹向 0 到 i-1 中任意弹簧或者 i+jump[i] 的弹簧(若 i+jump[i]>=N ,则表示小球弹出了机器)。小球位于编号 0 处的弹簧时不能再向左弹。
为了获得奖励,你需要将小球弹出机器。请求出最少需要按动多少次弹簧,可以将小球从编号 0 弹簧弹出整个机器,即向右越过编号 N-1 的弹簧。
示例 1:
输入:jump = [2, 5, 1, 1, 1, 1]
输出:3
解释:小 Z 最少需要按动 3 次弹簧,小球依次到达的顺序为 0 -> 2 -> 1 -> 6,最终小球弹出了机器。
限制:
1 <= jump.length <= 10^6
1 <= jump[i] <= 10000
解题思路
有两种思路可以参考,第一种是bfs,然后就是dp。按照大佬们的说法,看到找最短路径直接想到bfs,看到跳跃可以想到dp。果然,我还是只是个经验宝宝。
那么就分别来看这两个算法是如何实现的。
广度搜索算法(BFS)
BFS利用队列,DFS利用栈。利用队列可以实现广度搜索。然而在用了队列之后,你会发现,竟然超时了,那么此时,是选择优化还是肝dp呢?
至于怎么优化BFS,可以从广度搜索这个算法入手,首先需要为什么会出现超时这个问题。
广度搜索是将每次每个位置的全部左边的位置以及右边跳到的一个位置。
这样的话,可以发现问题所在,右边的位置没有问题,但是左边的位置被重复遍历。
所以需要一个判断,判断左边已经被遍历不再重复被添加到队列中
记录一个值为左边下一个该进队的节点,之后判断该节点左边的不入队,右边的入队然后更新下一个该进队的节点。
动态规划(DP)
在解题中,其实我的想法就是动态规划,但是难点不清楚怎么去动态转移。可以这么想,我们从右往左查找,当我找到第一个能出去的节点之后,那么这个节点右边的点就只需要往左移到这个点然后就可以出去了。但是苦于没办法将这个状态往左转移下去。
后面理了理思路,通过从后往前遍历节点,用数组dp[i]记录节点下标以及该节点下标跳出去需要的步数。
因为步数总是大于1的,所以能够保证从最后一个节点肯定是能跳出去的。而前面的节点跳的步数结果无外乎两种情况,一是直接跳出去,步数为1;二是跳到dp[i+jump[i]],则步数为该节点的步数+1。
但是问题没有这么简单,我们需要统计的是最小跳跃次数。所以
对于往前遍历一次,需要更新该节点和该节点跳到的节点之间所有节点的状态也就是值。
可以这么理解:(以示例 1为例)
从后往前一直到节点1,当这个节点执行跳跃的时候,我们需要更新这个跳跃之间节点的状态。
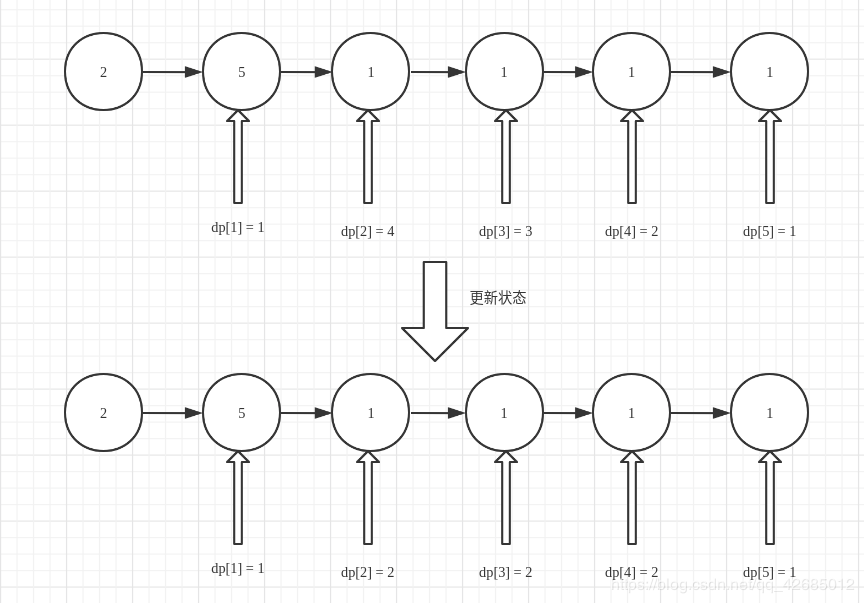
AC代码
//bfs
class Solution {
public:
int minJump(vector& jump) {
int res = 0;
queue q;
//初始化,从0开始
q.push(0);
//记录左边下一个该进队的节点
int maxpos = 1;
while(!q.empty()) {
int num = q.size();
for(int i = 0; i = jump.size()) return res + 1;
if(len >= maxpos) q.push(len);
for(int j = maxpos; j < pos; ++j) q.push(j);
maxpos = max(maxpos,pos+1);
}
res++;
}
return res;
}
};
//DP
class Solution {
public:
int minJump(vector& jump) {
int dp[jump.size()];
memset(dp, 0, sizeof(dp));
for(int pos = jump.size() - 1; pos >= 0; --pos) {
if(pos + jump[pos] >= jump.size()) dp[pos] = 1;
else dp[pos] = dp[pos + jump[pos]] + 1;
//当有跳跃的时候更新状态
if(jump[pos] > 1) {
//更新的时候需要保证节点始终在jump以及跳跃区间内,且改节点的值是大于跳跃节点的值
for(int i = pos + 1; i < jump.size() && i dp[pos]; ++i)
dp[i] = dp[pos] + 1;
}
}
return dp[0];
}
};
5. 二叉树任务调度
任务调度优化是计算机性能优化的关键任务之一。在任务众多时,不同的调度策略可能会得到不同的总体执行时间,因此寻求一个最优的调度方案是非常有必要的。
通常任务之间是存在依赖关系的,即对于某个任务,你需要先完成他的前导任务(如果非空),才能开始执行该任务。我们保证任务的依赖关系是一棵二叉树,其中 root 为根任务,root.left 和 root.right 为他的两个前导任务(可能为空),root.val 为其自身的执行时间。
在一个 CPU 核执行某个任务时,我们可以在任何时刻暂停当前任务的执行,并保留当前执行进度。在下次继续执行该任务时,会从之前停留的进度开始继续执行。暂停的时间可以不是整数。
现在,系统有两个 CPU 核,即我们可以同时执行两个任务,但是同一个任务不能同时在两个核上执行。给定这颗任务树,请求出所有任务执行完毕的最小时间。
示例 1:

输入:root = [47, 74, 31]
输出:121
解释:根节点的左右节点可以并行执行31分钟,剩下的43+47分钟只能串行执行,因此总体执行时间是121分钟。
示例 2:
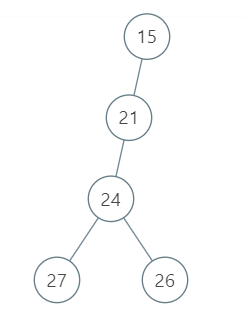
输入:root = [15, 21, null, 24, null, 27, 26]
输出:87
示例 3:
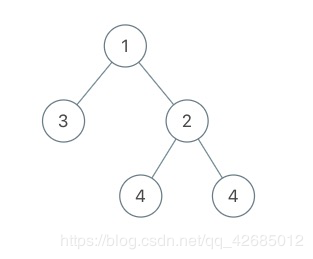
输入:root = [1,3,2,null,null,4,4]
输出:7.5
限制:
1 <= 节点数量 <= 1000
1 <= 单节点执行时间 <= 1000
解题思路
如果题目的意思没理解清楚,然后看示例。相信大概率会和我当时看这个题目一样,会有这样一个过程,看到示例1和示例2,觉得有思路了。看到示例3,懵逼。
这道题的意思是让双cpu尽可能的发挥其作用,也就是让其并行更可能多的时间。
需要注意的几个点:
其中比较重要的是第二点,然后依据第二点可以推断出,这道题的最优解肯定是先并行执行然后串行执行,因为根节点肯定是串行执行的。
如果能够求出最大的并行时间,那么这道题的答案就是所有节点时间总和(total)-最大的并行时间
那么如何去求得最大的并行时间呢?
设一颗任务树的左子树所有任务时间和为a,并行执行的时间为b,右子树分别为c,d。
那么理想状态下左右子树最大并行时间为(a+c)/2,也就是两个cpu一直在并行运行,此时该任务树的时间为:total - (a+c)/2,又因为total = root.val + a + c;所以该任务树的时间为:root.val + (a+c)/2。
但是会出现像示例1这样的情况(a-2b > c),一个cpu必须得等待,两个cpu不能做到同时运行,此时改任务树的时间为:total - (b+c),化简为:root.val + a - b。
理想状态,任务树的时间为:root.val + (a+c)/2。
(c-2d>a)的情况,任务树的时间为:root.val + c - d。
可以观察到(a-b)是根任务树左儿子的最优解,(c-d)是根任务树右儿子的最优解。递归完美解决
为了得到一个统一的结论而不是分条件的去计算,最后可以总结任务树的时间为:res(root)=max(res(root.left), res(root.right), (a+c)/2) + root.val;
AC代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
//pair.first记录当前节点总时间,pair.second记录最优解
pair res(TreeNode *root) {
if(root == NULL) return {0, 0};
auto l = res(root->left);
auto r = res(root->right);
return {l.first+r.first+root->val, root->val + max(max(l.second, r.second), (l.first+r.first)/2.0)};
}
double minimalExecTime(TreeNode* root) {
return res(root).second;
}
};
作者:胖狗子修行之路