基于动态规划思想的编辑距离计算

Irma ·

更新时间:2024-11-11

· 539 次阅读

编辑距离：

给定两文本或句子，计算需要多少步操作能够从一个句子转换为另外一个句子，允许操作有增加、删除和替换。距离越小，说明二者越相似，距离与大，说明二者差距越大。

利用动态规划计算编辑距离，其模型如下：

对于两个字符串a和b，计算两个字符串的相似度，即计算两个字符串的编辑距离，相当于计算它们字串的编辑距离，再加上从子串到全串所需的最少编辑次数即可，不断地进行递推。

递推公式如下：
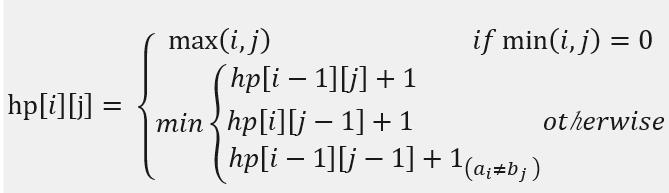
在这里插入图片描述
hp[i][j]指的是a的前i个字符和b中前j个字符之间的距离，字符串计算从index = 1开始（实际预算需要在字符串前补0），最终编辑距离为i=|a|,j=|b|时的hp[i][j]。
当min⁡(i,j)=0时，对应着字符串a的前i个字符和字符串b的前j个字符，因此时i，j中有一个值为0，表示a和b中有一个子串为空，则从a转换为b只需要进行max⁡(i,j)次字符编辑操作即可，所以它们之间的编辑距离为max⁡(i,j)，即i，j中的最大者。

当max⁡(i,j)≠0）时，hp[i][j]为如下三种情况最小值：
1、hp[i-1][j]+1 表示删除a_i ;
2、hp[i][j-1]+1 表示插入b_j；
3、hp[i-1][j-1]+1_(a_i≠b_j) 表示替换b_j。

公式中的1_(a_i≠b_j)为一个指示函数，当a_i=b_j时，表示字符串相同，指示函数取0；当a_i ≠b_j时，表示字符串不同，指示函数取1。

python3代码如下：

# 基于动态规划方法的编辑距离计算
def edit_dist(str1,str2):
    m,n = len(str1),len(str2)
    dp = [[0 for x in range(n+1)] for x in range(m+1)]
    for i in range(m+1):
        for j in range(n+1):
        # 第一个字符串为空
            if i == 0:
                dp[i][j] = j
        # 第二个字符串为空
            elif j == 0:
                dp[i][j] = i
            # 最后一个字符相同，不会产生代价
            elif str1[i-1] == str2[j-1]:
                dp[i][j] = dp[i-1][j-1]
            else:
                # insert remove replace
                dp[i][j] = 1 + min(dp[i][j-1],
                                   dp[i-1][j],
                                   dp[i-1][j-1]       
                                    )
#    print(dp)
    return dp[m][n]
str1 = 'abc'
str2 = 'dabc'
print('answer:',edit_dist(str1, str2))
# answer: 1

至此，编辑距离计算介绍完毕，后续会继续发布自然语言处理、知识图谱领域相关技术文档，望关注。

作者：华理小波哥

编辑距离动态规划动态

1024 个赞