洛谷题解——P1443:马的遍历
洛谷,https://www.luogu.com.cn/problem/P1443。
题目描述有一个 n*m 的棋盘 (1 < n, m <= 400),在某个点上有一个马,要求你计算出马到达棋盘上任意一个点最少要走几步?
输入格式一行四个数据,棋盘的大小和马的坐标。
输出格式一个 n*m 的矩阵,代表马到达某个点最少要走几步(左对齐,宽 5 格,不能到达则输出 -1)。
输入样例
3 3 1 1
输出样例
0 3 2
3 -1 1
2 1 4
题目分析
题意分析
告诉我们一个棋盘大小为 n*m,再告诉我们一个起点坐标 x,y。要求我们算出到棋盘所有点最少要走几步。
从最少这个字可以看出,本题可以考虑使用 BFS 来实现。
样例数据分析
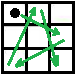
根据样例输入,我们知道棋盘大小为 3*3,开始位置为 1,1。注意,本题开始的不是零。下面我们来绘制一下到各个点需要的最少步数。我们知道不管国际象棋还是中国象棋,马都是走“日”字。如下图所示:
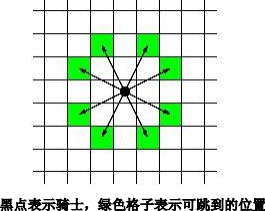
也就是说,马的可能走法有 8 种。可以参考如下定义方式:
//坐标定义
typedef struct _POS {
int x, y;
} POS;
//马所有移动方式定义
const POS moves[] = {{1,-2}, {2,-1},{2,1},{1,2},{-1,2},{-2,1},{-2,-1},{-1,-2}};
1,1 点
就是自己,自然不需要移动已经到了,也就是说输出 0。
2,1 点
从 1,1 出发要到 2,1 ,移动的方法如下图所示:1,1 -> 3,2 -> 1,3 -> 2,1,这样一共走了 3 次。
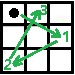
3,1 点
从 1,1 出发要到 3,1 ,移动的方法如下图所示:1,1 -> 2,3 -> 3,1,这样一共走了 2 次。

1,2 点
从 1,1 出发要到 1,2 ,移动的方法如下图所示:1,1 -> 2,3 -> 3,1 -> 1,2,这样一共走了 3 次。

2,2 点
从 1,1 出发要到 2,2 ,不管怎么走都没法走到,这样输出 -1。
3,2 点
从 1,1 出发要到 3,2 ,移动的方法如下图所示:1,1 -> 3,2,这样一共走了 1 次。
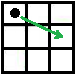
1,3 点
从 1,1 出发要到 1,3 ,移动的方法如下图所示:1,1 -> 3,2 -> 1,3,这样一共走了 2 次。
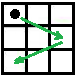
2,3 点
从 1,1 出发要到 2,3 ,移动的方法如下图所示:1,1 -> 2,3,这样一共走了 1 次。

3,3 点
从 1,1 出发要到 3,3 ,移动的方法如下图所示:1,1 -> 3,2 -> 1,3 -> 2,1 -> 3,3,这样一共走了 4 次。
从上面分析可知,最终的输出结果为:
0 3 2
3 -1 1
2 1 4
因此,只需要使用 BFS 遍历 n*m 棋盘的所有点,记录每个点到起点的距离即可。
编程思路
从上面的数据分析中,我们可以得出,本题是一个 BFS 的模板题。
1、读入数据。
2、从指定起点开始使用 BFS 遍历矩阵,记录所有位置到起点的距离。
3、输出距离。
AC 参考代码
#include
#include
#include
const int MAXN = 4e2+2;
struct MAZE {
int row, col;
int x1, y1;
bool visit[MAXN][MAXN];//
int dis[MAXN][MAXN];
};
struct POS {
int x, y;
};
void bfs(MAZE &maze) {
//压入起点
POS cur;
cur.x = maze.x1;
cur.y = maze.y1;
maze.dis[maze.x1][maze.y1] = 0;
maze.visit[maze.x1][maze.y1]=true;
std::queue q;
q.push(cur);
POS next;
const POS move[] = {{1,-2},{2,-1},{2,1},{1,2},{-1,2},{-2,1},{-2,-1},{-1,-2}};//移动方法
int i;
while (q.empty() != true) {
//遍历
cur = q.front();
q.pop();
//开始移动
for (i=0; i=1&&next.x=1&&next.y<=maze.col&&maze.visit[next.x][next.y]==false) {
maze.dis[next.x][next.y] = maze.dis[cur.x][cur.y] + 1;
maze.visit[next.x][next.y]=true;
q.push(next);
}
}
}
}
int main() {
//freopen("4.out", "w", stdout);
MAZE maze = {};
scanf("%d %d %d %d", &maze.row, &maze.col, &maze.x1, &maze.y1);
memset((void*)maze.dis, -1, sizeof(maze.dis));//将起点到所有点距离设置为-1
bfs(maze);
int i, j;
for (i=1; i<=maze.row; i++) {
for (j=1; j<=maze.col; j++) {
printf("%-5d", maze.dis[i][j]);
}
printf("\n");
}
//fclose(stdout);
return 0;
}
程序解读
1、由于题目输出有格式要求,即左对齐,宽 5 格。因此使用 printf 比较简单。代码如下:
printf("%-5d", xxxxxx);
其中 - 表示左对齐,5 表示占位格数。
2、关于无法到达点距离问题。这个问题有两个解决方法。
方案一:开始的时候,将所有点到起点的距离设置为 -1。通过 BFS 遍历一次棋盘后,所有不能到达的位置距离自然不会变化。代码如下:
memset((void*)maze.dis, -1, sizeof(maze.dis));
方案二:输出的时候配合 vis 矩阵,所有距离为 0 的点,如果 vis[i][j] 对应的值为 false,说明无法访问到,输出 -1 即可。代码如下:
for (i=1; i<=maze.row; i++) {
for (j=1; j<=maze.col; j++) {
if (false == maze.vis[i][j]) {
//需要排除起点
if (i==maze.x1 && j==maze.y1) {
//起点
printf("%-5d", 0);
} else {
printf("%-5d", -1);
}
} else {
printf("%-5d", maze.dis[i][j]);
}
}
printf("\n");
}
作者:努力的老周