Day5_贝叶斯分类器
贝叶斯定理是关于随机事件A和B的条件概率的一则定理。
P(A∣B)=P(B∣A)P(A)P(B){\displaystyle P(A\mid B)={\frac {P(B\mid A)P(A)}{P(B)}}}P(A∣B)=P(B)P(B∣A)P(A)
其中A{\displaystyle A}A以及B{\displaystyle B}B为随机事件,且P(B){\displaystyle P(B)}P(B)不为零。P(A∣B){\displaystyle P(A|B)}P(A∣B)是指在事件B{\displaystyle B}B发生的情况下事件A{\displaystyle A}A发生的概率。
在贝叶斯定理中,每个名词都有约定俗成的名称:
P(A∣B){\displaystyle P(A|B)}P(A∣B)是已知B{\displaystyle B}B发生后,A{\displaystyle A}A的条件概率。也由于得自B{\displaystyle B}B的取值而被称作A{\displaystyle A}A的后验概率。
P(A){\displaystyle P(A)}P(A)是A{\displaystyle A}A的先验概率(或边缘概率)。之所以称为"先验"是因为它不考虑任何B{\displaystyle B}B方面的因素。
P(B∣A){\displaystyle P(B|A)}P(B∣A)知A{\displaystyle A}A发生后,B{\displaystyle B}B的条件概率。也由于得自A{\displaystyle A}A的取值而被称作B{\displaystyle B}B的后验概率。
P(B){\displaystyle P(B)}P(B)是B{\displaystyle B}B的先验概率。
按这些术语,贝叶斯定理可表述为:
后验概率=(似然性∗先验概率)/标准化常量后验概率 = (似然性*先验概率)/标准化常量后验概率=(似然性∗先验概率)/标准化常量
也就是说,后验概率与先验概率和相似度的乘积成正比。
另外,比例P(B∣A)/P(B){\displaystyle P(B|A)/P(B)}P(B∣A)/P(B)被称作标准似然度(standardised—likelihoodstandardised — likelihoodstandardised—likelihood),贝叶斯定理可表述为:
后验概率=标准似然度∗先验概率后验概率 = 标准似然度*先验概率后验概率=标准似然度∗先验概率
所以将上述贝叶斯定理应用于分类问题上:
egegeg:有n个特征x1,x2,...,xnx_1,x_2, ...,x_nx1,x2,...,xn,将分类为yiy_iyi
P(yi∣x1,x2,...,xn)=P(x1,x2,...,xn∣yi)P(yi)P(x1,x2,...,xn){\displaystyle P(y_i\mid x_1,x_2, ...,x_n)={\frac {P(x_1,x_2, ...,x_n\mid y_i)P(y_i)}{P(x_1,x_2, ...,x_n)}}}P(yi∣x1,x2,...,xn)=P(x1,x2,...,xn)P(x1,x2,...,xn∣yi)P(yi)
贝叶斯定理假设每个输入变量都依赖于所有其他变量。这是计算复杂的原因。我们可以删除此假设,并认为每个输入变量彼此独立。
这将模型从依赖条件概率模型更改为独立条件概率模型,从而大大简化了计算。
首先,将分母从计算P(x1,x2,…,xn)P(x_1,x_2,…,x_n)P(x1,x2,…,xn)中删除,因为它是用于计算给定实例的每个类别的条件概率的常数,并且具有将结果归一化的效果。
P(yi∣x1,x2,...,xn)=P(x1,x2,...,xn∣yi)P(yi){\displaystyle P(y_i\mid x_1,x_2, ...,x_n)={ {P(x_1,x_2, ...,x_n\mid y_i)P(y_i)}}}P(yi∣x1,x2,...,xn)=P(x1,x2,...,xn∣yi)P(yi)
接下来,将给定类别标签的所有变量的条件概率更改为给定类别标签的每个变量值的独立条件概率。然后将这些独立的条件变量相乘。例如:
P(yi∣x1,x2,…,xn)=P(x1∣yi)∗P(x2∣yi)∗…P(xn∣yi)∗P(yi)P(y_i | x_1,x_2,…,x_n)= P(x_1 | y_i)* P(x_2 | y_i)*…P(x_n | y_i)* P(y_i)P(yi∣x1,x2,…,xn)=P(x1∣yi)∗P(x2∣yi)∗…P(xn∣yi)∗P(yi)
可以对每个类别标签执行此计算,并且可以选择概率最大的标签作为给定实例的分类。此决策规则称为最大后验决策规则。
贝叶斯定理的这种简化很普遍,广泛用于分类预测建模问题,通常被称为朴素贝叶斯。
如何计算呢?先验P(yi)P(y_i)P(yi)的计算很简单。可以通过将训练数据集中具有该类标签的观察数除以训练数据集中示例(行)的总数来估算。例如:
P(yi)=包含yi的示例/总共的示例P(y_i)=包含yi的示例/总共的示例P(yi)=包含yi的示例/总共的示例
给定类别标签的特征值的条件概率也可以从数据中估算出来。具体来说,属于给定类的数据示例,每个变量一个数据分布。这意味着,如果有K个类和n个变量,则必须创建和维护k * n个不同的概率分布。
根据每个特征的数据类型,需要使用不同的方法。具体而言,该数据用于估计三个标准概率分布之一的参数。
对于分类变量(例如计数或标签),可以使用多项式分布。如果变量是二进制变量,例如“是/否”或“真/假”,则可以使用二项分布。如果变量是数字变量(例如测量值),则通常使用高斯分布。
Binary: Binomial distribution.
Categorical: Multinomial distribution.
Numeric: Gaussian distribution.
下面通过使用PYTHON代码进行演示
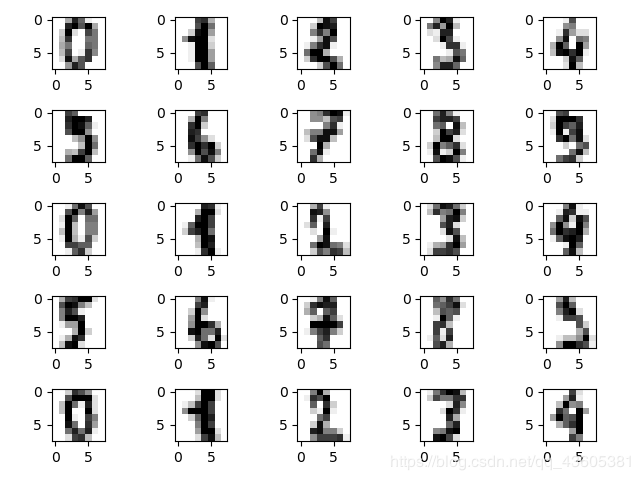
CODES首先加载数据集,并把数据集表示出来首先加载数据集,并把数据集表示出来
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
digits = load_digits()
fig = plt.figure()
print('vector from images 0:',digits.data[0])
"""
vector from images 0:
[ 0. 0. 5. 13. 9. 1. 0. 0. 0. 0. 13. 15. 10. 15. 5. 0. 0. 3.
15. 2. 0. 11. 8. 0. 0. 4. 12. 0. 0. 8. 8. 0. 0. 5. 8. 0.
0. 9. 8. 0. 0. 4. 11. 0. 1. 12. 7. 0. 0. 2. 14. 5. 10. 12.
0. 0. 0. 0. 6. 13. 10. 0. 0. 0.]
"""
for i in range(25):
ax = fig.add_subplot(5,5,i+1)
ax.imshow(digits.images[i],cmap=plt.cm.gray_r,interpolation='nearest')
plt.show()
#将数据分成训练集和测试集
X_train,X_test,y_train,y_test=train_test_split(digits.data,digits.target,test_size=0.2,random_state=0)
#数据使用方法
"""
fit(X,Y):在数据集(X,Y)上拟合模型。
get_params():获取模型参数。
predict(X):对数据集X进行预测。
predict_log_proba(X):对数据集X预测,得到每个类别的概率对数值。predict_proba(X):对数据集X预测,得到每个类别的概率。
score(X,Y):得到模型在数据集(X,Y)的得分情况。
"""
高斯朴素贝叶斯
高斯朴素贝叶斯算法是假设特征的可能性(即概率)为高斯分布。
class sklearn.naive_bayes.GaussianNB(priors=None)
priors:先验概率大小,如果没有给定,模型则根据样本数据自己计算(利用极大似然法)。
对象
class_prior_:每个样本的概率
class_count:每个类别的样本数量_
theta:每个类别中每个特征的均值
sigma_:每个类别中每个特征的方差
from sklearn.naive_bayes import GaussianNB
cls=GaussianNB().fit(X_train,y_train)
print("GaussianNB Training score:{:.2f}".format(cls.score(X_train,y_train)))
print("GaussianNB Test score:{:.2f}".format(cls.score(X_test,y_test)))
"""
GaussianNB Training score:0.86
GaussianNB Test score:0.82
"""
多项式分布贝叶斯
适用于服从多项分布的特征数据。
class sklearn.naive_bayes.MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)
alpha:先验平滑因子,默认等于1,当等于1时表示拉普拉斯平滑。
fit_prior:是否去学习类的先验概率,默认是True
class_prior:各个类别的先验概率,如果没有指定,则模型会根据数据自动学习, 每个类别的先验概率相同,等于类标记总个数N分之一。
对象
class_log_prior_:每个类别平滑后的先验概率
intercept_:是朴素贝叶斯对应的线性模型,其值和class_log_prior_相同
feature_log_prob_:给定特征类别的对数概率(条件概率)。 特征的条件概率=(指定类下指定特征出现的次数+alpha)/(指定类下所有特征出现次数之和+类的可能取值个数*alpha)
coef_: 是朴素贝叶斯对应的线性模型,其值和feature_log_prob相同
class_count_: 训练样本中各类别对应的样本数
feature_count_: 每个类别中各个特征出现的次数
from sklearn.naive_bayes import MultinomialNB
mul=MultinomialNB().fit(X_train,y_train)
print("MulitonmialNB Training score:{:.2f}".format(mul.score(X_train,y_train)))
print("MultionmialNB test score:{:.2f}".format(mul.score(X_test,y_test)))
"""
MulitonmialNB Training score:0.90
MultionmialNB test score:0.91
"""
伯努利朴素贝叶斯
BernoulliNB(Bernoulli Naive Bayes Classifier)
用于多重伯努利分布的数据,即有多个特征,但每个特征都假设是一个二元 (Bernoulli, boolean) 变量。
class sklearn.naive_bayes.BernoulliNB(alpha=1.0, binarize=0.0, fit_prior=True, class_prior=None)
alpha:平滑因子,与多项式中的alpha一致。
binarize:样本特征二值化的阈值,默认是0。如果不输入,则模型会认为所有特征都已经是二值化形式了;如果输入具体的值,则模型会把大于该值的部分归为一类,小于的归为另一类。
fit_prior:是否去学习类的先验概率,默认是True
class_prior:各个类别的先验概率,如果没有指定,则模型会根据数据自动学习, 每个类别的先验概率相同,等于类标记总个数N分之一。
对象
class_log_prior_:每个类别平滑后的先验对数概率。
feature_log_prob_:给定特征类别的经验对数概率。
class_count_:拟合过程中每个样本的数量。
feature_count_:拟合过程中每个特征的数量。
from sklearn.naive_bayes import BernoulliNB
ber0=BernoulliNB().fit(X_train,y_train)
print("BernoulliNB Training score:{:.2f}".format(ber0.score(X_train,y_train)))
print("BernoulliNB test score :{:.2f}".format(ber0.score(X_test,y_test)))
"""
BernoulliNB Training score:0.87
BernoulliNB test score :0.84
"""
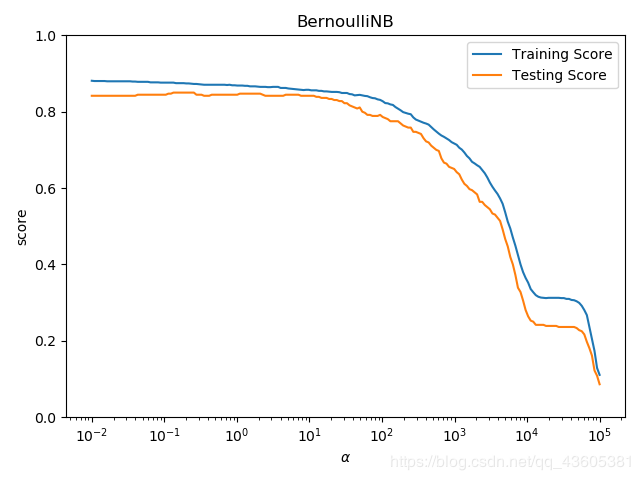
# 检验不同的alpha对伯努利贝叶斯分类器的预测性能的影响
alphas = np.logspace(-2,5,num=200)
train_scores = []
test_scores = []
for alpha in alphas:
ber = BernoulliNB(alpha=alpha)
ber.fit(X_train,y_train)
train_scores.append(ber.score(X_train,y_train))
test_scores.append(ber.score(X_test,y_test))
##绘图
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.plot(alphas,train_scores,label='Training Score')
ax.plot(alphas,test_scores,label='Testing Score')
ax.set_xlabel(r'$\alpha$')
ax.set_ylabel('score')
ax.set_ylim(0,1.0)
ax.set_title('BernoulliNB')
ax.set_xscale('log')
ax.legend(loc='best')
plt.show()
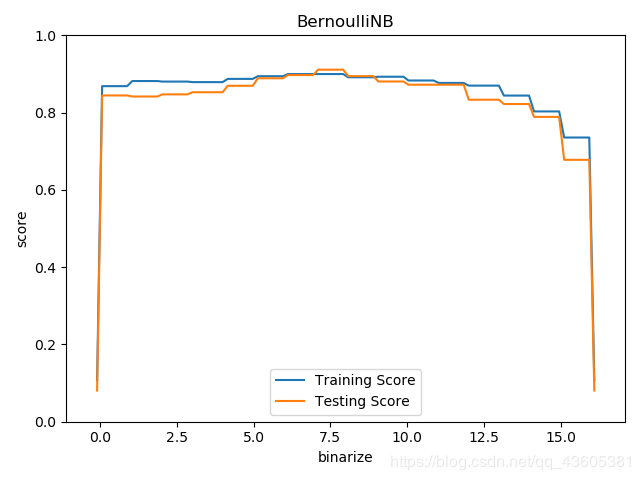
# 考虑binarize参数对伯努利贝叶斯分类器的影响
min_x = min(np.min(X_train.ravel()),np.min(X_test.ravel())) - 0.1
max_x = max(np.max(X_train.ravel()),np.max(X_test.ravel())) + 0.1
binarizes = np.linspace(min_x,max_x,endpoint=True,num=100)
train_scores = []
test_scores = []
for binarize in binarizes:
cls = BernoulliNB(binarize=binarize)
cls.fit(X_train,y_train)
train_scores.append(cls.score(X_train,y_train))
test_scores.append(cls.score(X_test,y_test))
#绘图
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.plot(binarizes,train_scores,label='Training Score')
ax.plot(binarizes,test_scores,label='Testing Score')
ax.set_xlabel('binarize')
ax.set_ylabel('score')
ax.set_ylim(0,1.0)
ax.set_xlim(min_x-1,max_x+1)
ax.set_title('BernoulliNB')
ax.legend(loc='best')
plt.show()
《Python机器学习基础教程》 人 民 邮 电 出 版 社
维基百科
作者:AU20190909