基于感知机Perceptron的鸢尾花分类实践

Veronica ·

更新时间:2024-11-10

· 537 次阅读

文章目录1. 感知机简介2. 编写感知机实践2.1 数据处理2.2 编写感知机类2.3 多参数组合运行3. sklearn 感知机实践4. 附完整代码
本文将使用感知机模型，对鸢尾花进行分类，并调整参数，对比分类效率。 1. 感知机简介

感知机（perceptron）是二类分类的线性分类模型

输入：实例的特征向量输出：实例的类别，取 +1 和 -1 二值感知机对应于输入空间（特征空间）中将实例划分为正负两类的分离超平面，属于判别模型旨在求出将训练数据进行线性划分的分离超平面，为此，导入基于误分类的损失函数，利用梯度下降法对损失函数进行极小化，求得感知机模型。感知机学习算法具有简单而易于实现的优点，分为原始形式和对偶形式。预测：对新的输入进行分类

具体内容见李航《统计学习方法》第二章，感知机读书笔记。

2. 编写感知机实践

本文代码参考了此处：fengdu78，本人添加了感知机算法的对偶形式，并对不同的参数下的迭代次数进行比较。

2.1 数据处理 数据采用sklearn内置的鸢尾花数据（数据介绍请参考此处）

# 读取鸢尾花数据
iris = load_iris()
# 将鸢尾花4个特征，以4列存入pandas的数据框架
df = pd.DataFrame(iris.data, columns=iris.feature_names)
# 在最后一列追加 加入标签（分类）列数据
df['lab'] = iris.target
# df.columns=[iris.feature_names[0], iris.feature_names[1], iris.feature_names[2], iris.feature_names[3], 'lab']
# df['lab'].value_counts()
# 选取前两种花进行划分（每种数据50组）
plt.scatter(df[:50][iris.feature_names[0]], df[:50][iris.feature_names[1]], label=iris.target_names[0])
plt.scatter(df[50:100][iris.feature_names[0]], df[50:100][iris.feature_names[1]], label=iris.target_names[1])
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])
# 选取数据,前100行，前两个特征，最后一列标签
data = np.array(df.iloc[:100, [0, 1, -1]])
# X是除最后一列外的所有列，y是最后一列
X, y = data[:, :-1], data[:, -1]
# 生成感知机的标签值，+1， -1, 第一种-1，第二种+1
y = np.array([1 if i == 1 else -1 for i in y])

2.2 编写感知机类

class PerceptronModel():
    def __init__(self, X, y, eta):
        self.w = np.zeros(len(X[0]), dtype=np.float)  # 权重
        self.b = 0  # 偏置
        self.eta = eta  # 学习率
        self.dataX = X  # 数据
        self.datay = y  # 标签
        self.iterTimes = 0  # 迭代次数
        # 对偶形式的参数
        self.a = np.zeros(len(X), dtype=np.float)  # alpha
        self.Gmatrix = np.zeros((len(X), len(X)), dtype=np.float)
        self.calculateGmatrix()  # 计算Gram矩阵
    def sign0(self, x, w, b):  # 原始形式sign函数
        y = np.dot(w, x) + b
        return y
    def sign1(self, a, G_j, Y, b):  # 对偶形式sign函数
        y = np.dot(np.multiply(a, Y), G_j) + b
        return y
    def OriginClassifier(self):  # 原始形式的分类算法
        self.iterTimes = 0
        self.b = 0
        stop = False
        while not stop:
            wrong_count = 0
            for i in range(len(self.dataX)):
                X = self.dataX[i]
                y = self.datay[i]
                if (y * self.sign0(X, self.w, self.b)) <= 0:
                    self.w += self.eta * np.dot(X, y)
                    self.b += self.eta * y
                    wrong_count += 1
                    self.iterTimes += 1
            if wrong_count == 0:
                stop = True
        print("原始形式，分类完成！步长：%.4f, 共迭代 %d 次" % (self.eta, self.iterTimes))
    def calculateGmatrix(self):  # 计算Gram矩阵
        for i in range(len(self.dataX)):
            for j in range(0, i + 1):  # 对称的计算一半就行
                self.Gmatrix[i][j] = np.dot(self.dataX[i], self.dataX[j])
                self.Gmatrix[j][i] = self.Gmatrix[i][j]
    def DualFormClassifier(self):  # 对偶形式分类算法
        self.iterTimes = 0
        self.b = 0
        stop = False
        while not stop:
            wrong_count = 0
            for i in range(len(self.dataX)):
                y = self.datay[i]
                G_i = self.Gmatrix[i]
                if (y * self.sign1(self.a, G_i, self.datay, self.b)) <= 0:
                    self.a[i] += self.eta
                    self.b += self.eta * y
                    wrong_count += 1
                    self.iterTimes += 1
            if wrong_count == 0:
                stop = True
        print("对偶形式，分类完成！步长：%.4f, 共迭代 %d 次" % (self.eta, self.iterTimes))

2.3 多参数组合运行

# 调用感知机进行分类，学习率eta
 perceptron = PerceptronModel(X, y, eta=0.3)
 perceptron.OriginClassifier()  # 原始形式分类
 # 绘制原始算法分类超平面
 x_points = np.linspace(4, 7, 10)
 y0 = -(perceptron.w[0] * x_points + perceptron.b) / perceptron.w[1]
 plt.plot(x_points, y0, 'r', label='原始算法分类线')
 perceptron.DualFormClassifier()  # 对偶形式分类
 # 由alpha，b 计算omega向量
 omega0 = sum(perceptron.a[i] * y[i] * X[i][0] for i in range(len(X)))
 omega1 = sum(perceptron.a[i] * y[i] * X[i][1] for i in range(len(X)))
 y1 = -(omega0 * x_points + perceptron.b) / omega1
 # 绘制对偶算法分类超平面
 plt.plot(x_points, y1, 'b', label='对偶算法分类线')
 plt.rcParams['font.sans-serif'] = 'SimHei'  # 消除中文乱码
 plt.legend()
 plt.show()

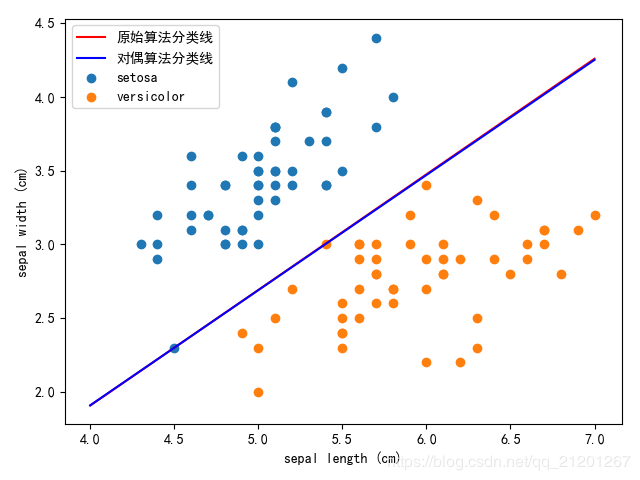
在这里插入图片描述

	原始算法	对偶算法
η=0.1\eta=0.1η=0.1	初值全0，迭代1518次，初值全1，迭代1473次	初值全0，迭代1488次，初值全1，迭代2378次
η=0.5\eta=0.5η=0.5	初值全0，迭代1562次，初值全1，迭代1472次	初值全0，迭代1518次，初值全1，迭代1325次
η=1\eta=1η=1	初值全0，迭代1562次，初值全1，迭代1486次	初值全0，迭代1518次，初值全1，迭代1367次

# ------------------学习率不同，查看迭代次数----------------------------
n = 100
i = 0
eta_iterTime = np.zeros((n, 3), dtype=float)
for eta in np.linspace(0.01, 1.01, n):
    eta_iterTime[i][0] = eta    # 第一列，学习率
    perceptron = PerceptronModel(X, y, eta)
    perceptron.OriginClassifier()
    eta_iterTime[i][1] = perceptron.iterTimes # 第二列，原始算法迭代次数
    perceptron.DualFormClassifier()
    eta_iterTime[i][2] = perceptron.iterTimes # 第三列，对偶算法迭代次数
    i += 1
x = eta_iterTime[:, 0]  # 数据切片
y0 = eta_iterTime[:, 1]
y1 = eta_iterTime[:, 2]
plt.scatter(x, y0, c='r', marker='o', label='原始算法')
plt.scatter(x, y1, c='b', marker='x', label='对偶算法')
plt.xlabel('步长(学习率)')
plt.ylabel('迭代次数')
plt.title("不同步长，不同算法形式下，迭代次数")
plt.legend()
plt.show()

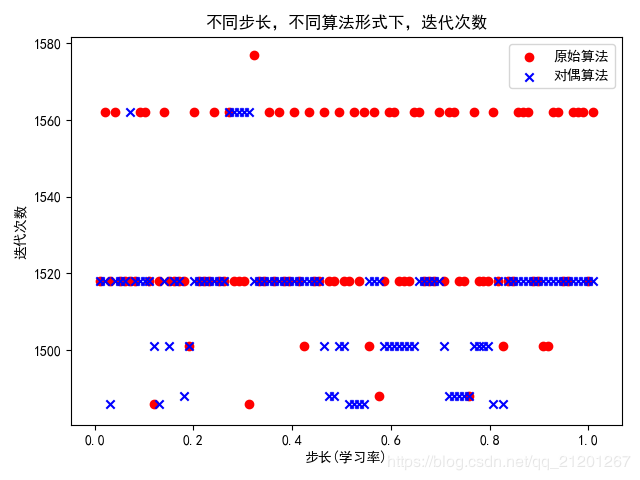
在这里插入图片描述
结论：

感知机的两种算法形式均会因为初值和学习率的不同，而造成的多种迭代路径从上面图标也印证了，对于线性可分的数据，感知机学习算法迭代是收敛的 3. sklearn 感知机实践

sklearn.linear_model.Perceptron 官网参数介绍

class sklearn.linear_model.Perceptron(penalty=None, alpha=0.0001, 
fit_intercept=True, max_iter=1000, tol=0.001, shuffle=True, 
verbose=0, eta0=1.0, n_jobs=None, random_state=0,
early_stopping=False,validation_fraction=0.1, 
n_iter_no_change=5, class_weight=None, warm_start=False)

classify = Perceptron(fit_intercept=True, max_iter=1000, shuffle=True, eta0=0.1, tol=None)
classify.fit(X, y)
print("特征权重：", classify.coef_)  # 特征权重 w
print("截距（偏置）:", classify.intercept_)  # 截距 b
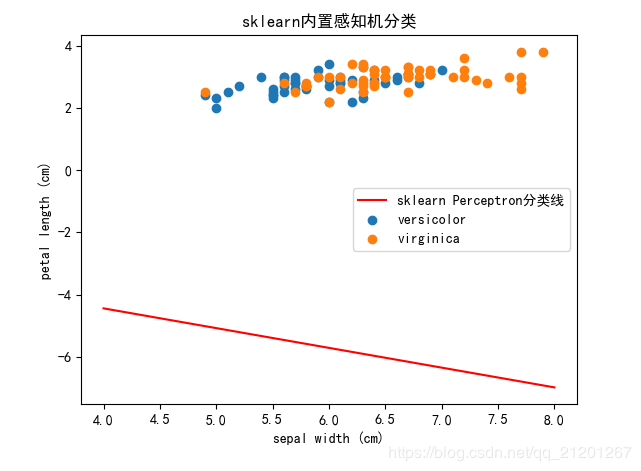
# 可视化
plt.scatter(df[:50][iris.feature_names[0]], df[:50][iris.feature_names[1]], label=iris.target_names[0])
plt.scatter(df[50:100][iris.feature_names[0]], df[50:100][iris.feature_names[1]], label=iris.target_names[1])
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])
# 绘制分类超平面
x_points = np.linspace(4, 7, 10)
y = -(classify.coef_[0][0] * x_points + classify.intercept_) / classify.coef_[0][1]
plt.plot(x_points, y, 'r', label='sklearn Perceptron分类线')
plt.title("sklearn内置感知机分类")
plt.legend()
plt.show()

运行结果：

特征权重： [[ 6.95 -8.73]]
截距（偏置）: [-11.2]

在这里插入图片描述

可以看出在这两个特征下，两种花线性可分，感知机将两类花分类成功

我们稍微更改下数据为后两种花，再次运行

在这里插入图片描述

可以看出，后两种花在这2个特征下线性不可分，感知机做出了错误分类线 4. 附完整代码

# -*- coding:utf-8 -*-
# @Python 3.7
# @Time: 2020/2/28 22:07
# @Author: Michael Ming
# @Website: https://michael.blog.csdn.net/
# @File: 2.perceptron.py
# @Reference: https://github.com/fengdu78/lihang-code
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron
import matplotlib.pyplot as plt
class PerceptronModel():
    def __init__(self, X, y, eta):
        self.w = np.zeros(len(X[0]), dtype=np.float)  # 权重
        self.b = 0  # 偏置
        self.eta = eta  # 学习率
        self.dataX = X  # 数据
        self.datay = y  # 标签
        self.iterTimes = 0  # 迭代次数
        # 对偶形式的参数
        self.a = np.zeros(len(X), dtype=np.float)  # alpha
        self.Gmatrix = np.zeros((len(X), len(X)), dtype=np.float)
        self.calculateGmatrix()  # 计算Gram矩阵
    def sign0(self, x, w, b):  # 原始形式sign函数
        y = np.dot(w, x) + b
        return y
    def sign1(self, a, G_j, Y, b):  # 对偶形式sign函数
        y = np.dot(np.multiply(a, Y), G_j) + b
        return y
    def OriginClassifier(self):  # 原始形式的分类算法
        self.iterTimes = 0
        self.b = 0
        stop = False
        while not stop:
            wrong_count = 0
            for i in range(len(self.dataX)):
                X = self.dataX[i]
                y = self.datay[i]
                if (y * self.sign0(X, self.w, self.b)) <= 0:
                    self.w += self.eta * np.dot(X, y)
                    self.b += self.eta * y
                    wrong_count += 1
                    self.iterTimes += 1
            if wrong_count == 0:
                stop = True
        print("原始形式，分类完成！步长：%.4f, 共迭代 %d 次" % (self.eta, self.iterTimes))
    def calculateGmatrix(self):  # 计算Gram矩阵
        for i in range(len(self.dataX)):
            for j in range(0, i + 1):  # 对称的计算一半就行
                self.Gmatrix[i][j] = np.dot(self.dataX[i], self.dataX[j])
                self.Gmatrix[j][i] = self.Gmatrix[i][j]
    def DualFormClassifier(self):  # 对偶形式分类算法
        self.iterTimes = 0
        self.b = 0
        stop = False
        while not stop:
            wrong_count = 0
            for i in range(len(self.dataX)):
                y = self.datay[i]
                G_i = self.Gmatrix[i]
                if (y * self.sign1(self.a, G_i, self.datay, self.b)) <= 0:
                    self.a[i] += self.eta
                    self.b += self.eta * y
                    wrong_count += 1
                    self.iterTimes += 1
            if wrong_count == 0:
                stop = True
        print("对偶形式，分类完成！步长：%.4f, 共迭代 %d 次" % (self.eta, self.iterTimes))
if __name__ == '__main__':
    # 读取鸢尾花数据
    iris = load_iris()
    # 将鸢尾花4个特征，以4列存入pandas的数据框架
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    # 在最后一列追加 加入标签（分类）列数据
    df['lab'] = iris.target
    # df.columns=[iris.feature_names[0], iris.feature_names[1], iris.feature_names[2], iris.feature_names[3], 'lab']
    # df['lab'].value_counts()
    # 选取前两种花进行划分（每种数据50组）
    plt.scatter(df[:50][iris.feature_names[0]], df[:50][iris.feature_names[1]], label=iris.target_names[0])
    plt.scatter(df[50:100][iris.feature_names[0]], df[50:100][iris.feature_names[1]], label=iris.target_names[1])
    plt.xlabel(iris.feature_names[0])
    plt.ylabel(iris.feature_names[1])
    # 选取数据,前100行，前两个特征，最后一列标签
    data = np.array(df.iloc[:100, [0, 1, -1]])
    # X是除最后一列外的所有列，y是最后一列
    X, y = data[:, :-1], data[:, -1]
    # 生成感知机的标签值，+1， -1, 第一种-1，第二种+1
    y = np.array([1 if i == 1 else -1 for i in y])
    # 调用感知机进行分类，学习率eta
    perceptron = PerceptronModel(X, y, eta=0.1)
    perceptron.OriginClassifier()  # 原始形式分类
    # 绘制原始算法分类超平面
    x_points = np.linspace(4, 7, 10)
    y0 = -(perceptron.w[0] * x_points + perceptron.b) / perceptron.w[1]
    plt.plot(x_points, y0, 'r', label='原始算法分类线')
    perceptron.DualFormClassifier()  # 对偶形式分类
    # 由alpha，b 计算omega向量
    omega0 = sum(perceptron.a[i] * y[i] * X[i][0] for i in range(len(X)))
    omega1 = sum(perceptron.a[i] * y[i] * X[i][1] for i in range(len(X)))
    y1 = -(omega0 * x_points + perceptron.b) / omega1
    # 绘制对偶算法分类超平面
    plt.plot(x_points, y1, 'b', label='对偶算法分类线')
    plt.rcParams['font.sans-serif'] = 'SimHei'  # 消除中文乱码
    plt.legend()
    plt.show()
    # ------------------学习率不同，查看迭代次数----------------------------
    n = 5
    i = 0
    eta_iterTime = np.zeros((n, 3), dtype=float)
    for eta in np.linspace(0.01, 1.01, n):
        eta_iterTime[i][0] = eta  # 第一列，学习率
        perceptron = PerceptronModel(X, y, eta)
        perceptron.OriginClassifier()
        eta_iterTime[i][1] = perceptron.iterTimes  # 第二列，原始算法迭代次数
        perceptron.DualFormClassifier()
        eta_iterTime[i][2] = perceptron.iterTimes  # 第三列，对偶算法迭代次数
        i += 1
    x = eta_iterTime[:, 0]  # 数据切片
    y0 = eta_iterTime[:, 1]
    y1 = eta_iterTime[:, 2]
    plt.scatter(x, y0, c='r', marker='o', label='原始算法')
    plt.scatter(x, y1, c='b', marker='x', label='对偶算法')
    plt.xlabel('步长(学习率)')
    plt.ylabel('迭代次数')
    plt.title("不同步长，不同算法形式下，迭代次数")
    plt.legend()
    plt.show()
    # ------------------sklearn实现----------------------------
    classify = Perceptron(fit_intercept=True, max_iter=10000, shuffle=False, eta0=0.5, tol=None)
    classify.fit(X, y)
    print("特征权重：", classify.coef_)  # 特征权重 w
    print("截距（偏置）:", classify.intercept_)  # 截距 b
    # 可视化
    plt.scatter(df[:50][iris.feature_names[0]], df[:50][iris.feature_names[1]], label=iris.target_names[0])
    plt.scatter(df[50:100][iris.feature_names[0]], df[50:100][iris.feature_names[1]], label=iris.target_names[1])
    plt.xlabel(iris.feature_names[0])
    plt.ylabel(iris.feature_names[1])
    # 绘制分类超平面
    x_points = np.linspace(4, 7, 10)
    y = -(classify.coef_[0][0] * x_points + classify.intercept_) / classify.coef_[0][1]
    plt.plot(x_points, y, 'r', label='sklearn Perceptron分类线')
    plt.title("sklearn内置感知机分类")
    plt.legend()
    plt.show()

作者：Michael阿明

鸢尾花分类花

1024 个赞