[从零构建光栅渲染器] 1.Bresenham 画线算法
非常感谢和推荐Sokolov的教程,Sokolov使用500行C++代码实现一个光栅渲染器。教程学习过程非常平滑,从画点、线和三角形开始教学,在逐步深入三维变换,投影,再到顶点着色器,片段着色器等等。教程地址:https://github.com/ssloy/tinyrenderer。Sokolov的教程为英文,我翻译了其文章。
在学习过程中,有些内容可能您可能云里雾里,这时就需要查阅《计算机图形学》的书籍了,这里面的算法和公式可以帮助您理解代码。
作者:憨豆酒(YinDou),联系我yindou97@163.com,熟悉图形学,图像处理领域,本章的源代码可在此仓库中找到https://github.com/douysu/person-summary:如果对您有帮助,还请给一个star,如果大家发现错误以及不合理之处,还希望多多指出。
我的知乎
我的Github
我的博客
 第一次尝试
第一次尝试
第一课的目标是渲染一个线形网格。为了画它,我们应该先学习如何去绘制线段。我们可以简单阅读以下Bresenham画线算法,但是让我们自己来写代码。应该怎么写一个从点(x0, y0)到点(x1, y1)的线段呢?
可以这样:
void line(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) {
for (float t=0.; t<1.; t+=.01) {
int x = x0 + (x1-x0)*t;
int y = y0 + (y1-y0)*t;
image.set(x, y, color);
}
}

代码在这里可以找到here
第二次尝试上面的代码问题是变量的选择(当然还有效率不高的问题)。我上面是让等于.01,如果改成.1,线段会成这样:
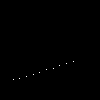
我们可以轻松找到其中重要的地方:仅仅是绘制像素的数目不同(第一次绘制的像素数目多,改变常量为.1后,绘制的像素变少),一种简单的方法如下:(其实不好的,错误的)
void line(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) {
for (int x=x0; x<=x1; x++) {
float t = (x-x0)/(float)(x1-x0);
int y = y0*(1.-t) + y1*t;
image.set(x, y, color);
}
}
警告!我的学生出现整数除法的错误,像(x - x0) / (x1 - x0)。因此,我们使用下面的代码会绘制出这样的直线:
line(13, 20, 80, 40, image, white);
line(20, 13, 40, 80, image, red);
line(80, 40, 13, 20, image, red);
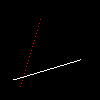
一条直线是正确的,第二条直线有很多洞,根本看不到第三条直线。注意:在这个代码中第一条和第三条直线的位置相同,颜色不相同,方向不相同。(起点和终点进行翻转)。我们看到了白色的线,它绘制的很好。我希望把这条白色的线转换成红色的,但是没有完成。对称测试:绘制线段时不应取决于顶点的顺序:(A, B)和(B, A)线段应该是一样的。
第三次尝试我们通过交换点来修复丢失的红线,使x0始终低于x1。
第二次尝试中,红色线段的高度大于宽度,因此有很多孔,不连续的地方。我的学生建议使用下面代码来修复:
if (dx>dy) {for (int x)} else {for (int y)}
天啊!
void line(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) {
bool steep = false;
if (std::abs(x0-x1)x1) { // make it left−to−right
std::swap(x0, x1);
std::swap(y0, y1);
}
for (int x=x0; x<=x1; x++) {
float t = (x-x0)/(float)(x1-x0);
int y = y0*(1.-t) + y1*t;
if (steep) {
image.set(y, x, color); // if transposed, de−transpose
} else {
image.set(x, y, color);
}
}
}
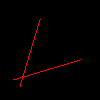
警告:编译器的优化器在创建高效的代码方面比你和我都好。我们应该注意,每个除法都有相同的除数。此部分是出于历史文化的原因。
这个代码工作的很好。这正是我在最终版本或渲染器中看到的那种复杂性。但其确实是非常低效的(因为有很多除法),但是它代码很短,可读性比较好。注意,代码没有使用断言,也没有检查是否超出边界,这非常不好。在这篇文章中,我要经常重复使用这块代码,我系统的检查了其必要性。
虽然之前的代码工作的很好,但是我们还可以优化。优化是一个危险的事情。我们应该清楚代码所运行的平台。针对GPU和CPU的优化是两种完全不同的事情。在优化之前,我们需要分析代码。考虑一下,哪个操作是比较消耗资源的。
测试:我执行了1000000次绘制之前的三条直线。我的CPU是Intel® Core™ i5-3450 CPU @ 3.10GHz. 对于每个像素,代码都调用了TGAColor的复制构造函数,总共像素数目=1000000 * 3(线段) * 50(每条线段像素数目)。我们应该从哪里开始优化?分析器会告诉我们。
我使用命令g++ -ggdb -g -pg -O0完成编译,然后运行gprof:
% cumulative self self total
time seconds seconds calls ms/call ms/call name
69.16 2.95 2.95 3000000 0.00 0.00 line(int, int, int, int, TGAImage&, TGAColor)
19.46 3.78 0.83 204000000 0.00 0.00 TGAImage::set(int, int, TGAColor)
8.91 4.16 0.38 207000000 0.00 0.00 TGAColor::TGAColor(TGAColor const&)
1.64 4.23 0.07 2 35.04 35.04 TGAColor::TGAColor(unsigned char, unsigned char, unsigned char, unsigned char)
0.94 4.27 0.04 TGAImage::get(int, int)
复制颜色话费了10%的时间,70%的时间花费在了绘制直线上!这正是咱们需要优化的地方。
继续第五次尝试我们应该注意到了每个除法都有相同的除数。让我们把它从循环里面拿出来。误差变量给出我们当前点(x, y)到直线的距离,每次误差大于一个像素的时候,我们将y增加或减小1,当然误差也需要增加减小1.
代码在这里here.
void line(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) {
bool steep = false;
if (std::abs(x0-x1)x1) {
std::swap(x0, x1);
std::swap(y0, y1);
}
int dx = x1-x0;
int dy = y1-y0;
float derror = std::abs(dy/float(dx));
float error = 0;
int y = y0;
for (int x=x0; x.5) {
y += (y1>y0?1:-1);
error -= 1.;
}
}
}
翻译作者内容:这里就是Bresenham画线算法了,如果您看不懂代码,请及时看一下《计算机图形学》Bresenham 画线算法的章节。
调试信息在这:
% cumulative self self total
time seconds seconds calls ms/call ms/call name
38.79 0.93 0.93 3000000 0.00 0.00 line(int, int, int, int, TGAImage&, TGAColor)
37.54 1.83 0.90 204000000 0.00 0.00 TGAImage::set(int, int, TGAColor)
19.60 2.30 0.47 204000000 0.00 0.00 TGAColor::TGAColor(int, int)
2.09 2.35 0.05 2 25.03 25.03 TGAColor::TGAColor(unsigned char, unsigned char, unsigned char, unsigned char)
1.25 2.38 0.03 TGAImage::get(int, int)
最后的尝试
为什么我们需要浮点数顶点呢?唯一的原因就是在循环体里用dx除以1和.5进行比较。我们可以通过换一个误差变量来去掉浮点顶点。让我们回顾error2,假设它等于error * dx * 2,这里是代码:
void line(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) {
bool steep = false;
if (std::abs(x0-x1)x1) {
std::swap(x0, x1);
std::swap(y0, y1);
}
int dx = x1-x0;
int dy = y1-y0;
int derror2 = std::abs(dy)*2;
int error2 = 0;
int y = y0;
for (int x=x0; x dx) {
y += (y1>y0?1:-1);
error2 -= dx*2;
}
}
}
% cumulative self self total
time seconds seconds calls ms/call ms/call name
42.77 0.91 0.91 204000000 0.00 0.00 TGAImage::set(int, int, TGAColor)
30.08 1.55 0.64 3000000 0.00 0.00 line(int, int, int, int, TGAImage&, TGAColor)
21.62 2.01 0.46 204000000 0.00 0.00 TGAColor::TGAColor(int, int)
1.88 2.05 0.04 2 20.02 20.02 TGAColor::TGAColor(unsigned char, unsigned char, unsigned char, unsigned char)
现在,只需要通过引用传递颜色就可以删除不必要的副本(或者使用编译 flag -O3)。注意代码中的乘法和除法,执行时间从2.95缩短了0.64。
我建议查看这个this issue。优化是棘手的!
线框渲染我们准备创建一个线框渲染器。在这里你可以找到代码code and the test model here。我使用wavefront obj格式文件来保存模型。我们需要从文件中读取到顶点数组,格式如下:
v 0.608654 -0.568839 -0.416318
x,y,z是坐标,每个面对应三个顶点,格式如下。
f 1193/1240/1193 1180/1227/1180 1179/1226/1179
翻译作者内容:以1193/1240/1193为例,1193对应顶点索引,1240是纹理坐标uv索引,1193是法向量索引,在后面会提到。也就是说这个面的三个顶点是第1193,1180,1179所对应的x,y,z。
在本篇文章,我们只需要读取空格后的第一个数字,也就是顶点坐标,纹理和法向量我们现在不关心。因此,1193, 1180 和 1179顶点组成一个三角形。注意obj文件的索引从1开始,也就意味着你需要分别从1192,1179和1178找到。model.cpp解析.obj文件。在主函数中写下如下代码,我们的线渲染就好了。
for (int i=0; infaces(); i++) {
std::vector face = model->face(i);
for (int j=0; jvert(face[j]);
Vec3f v1 = model->vert(face[(j+1)%3]);
int x0 = (v0.x+1.)*width/2.;
int y0 = (v0.y+1.)*height/2.;
int x1 = (v1.x+1.)*width/2.;
int y1 = (v1.y+1.)*height/2.;
line(x0, y0, x1, y1, image, white);
}
}

下一章我们将会绘制一个2D三角形来提高我们的渲染器。
作者:憨豆酒D