最优化计算入门基础

Posy ·

更新时间:2024-11-13

· 724 次阅读

最优化计算入门6个例子学习如何建造公式EXAMPLE1:MANIFACTURINGEXAMPLE2:TOYSEXAMPLE3:BEAMSEXAMPLE4:ANTENNASEXAMPLE5:RR ROBOTEXAMPLE6:RESOURCES ALLOCATIONMatlab代码基础格式 6个例子学习如何建造公式 EXAMPLE1:MANIFACTURING

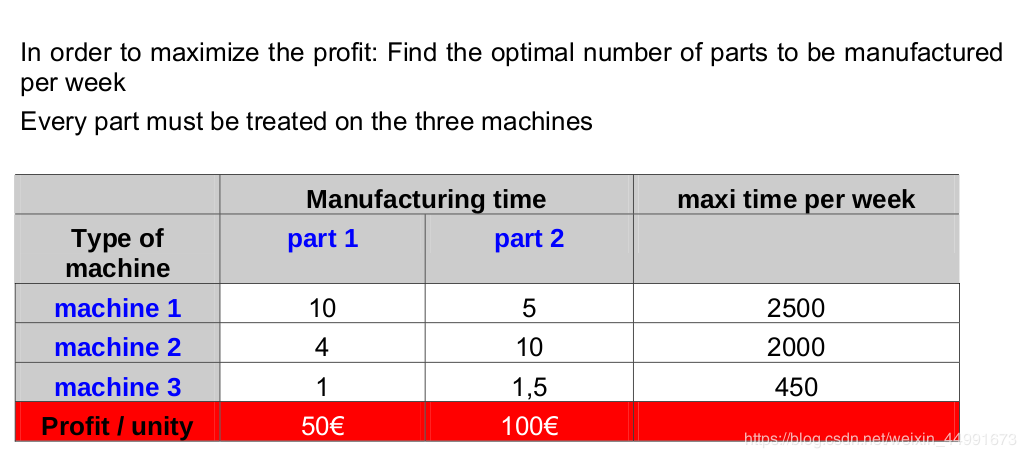
在这里插入图片描述
如何把一个现实应用问题用数学公式表达出来

EXAMPLE2:TOYS

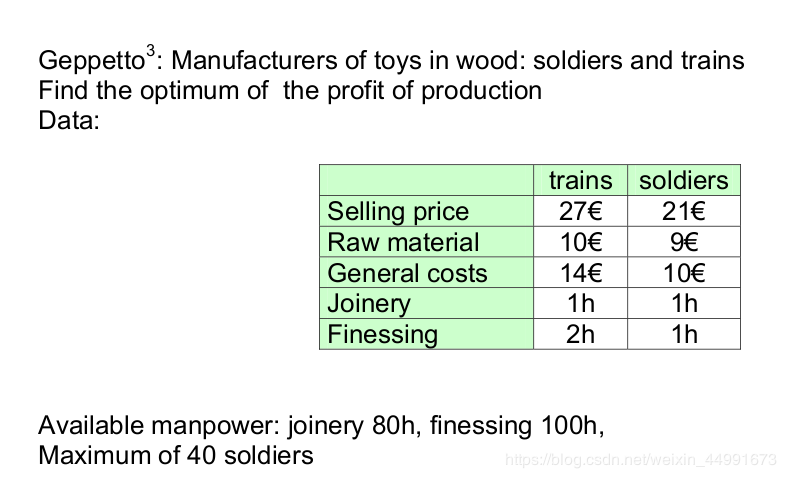
在这里插入图片描述
如何把一个繁琐复杂的数据表格重新规划

项目	Train	Soldiers	Max
g(1)	2	1	100
g(2)	1	1	80
g(3)	0	1	40
profit	3	2	?

EXAMPLE3:BEAMS

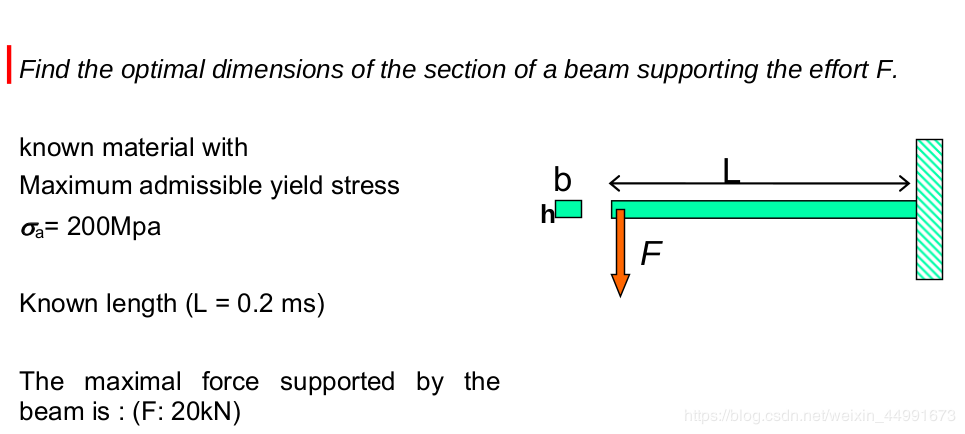
在这里插入图片描述
遇到诸如性能和成本这种矛盾变量时，如何衡量

EXAMPLE4:ANTENNAS

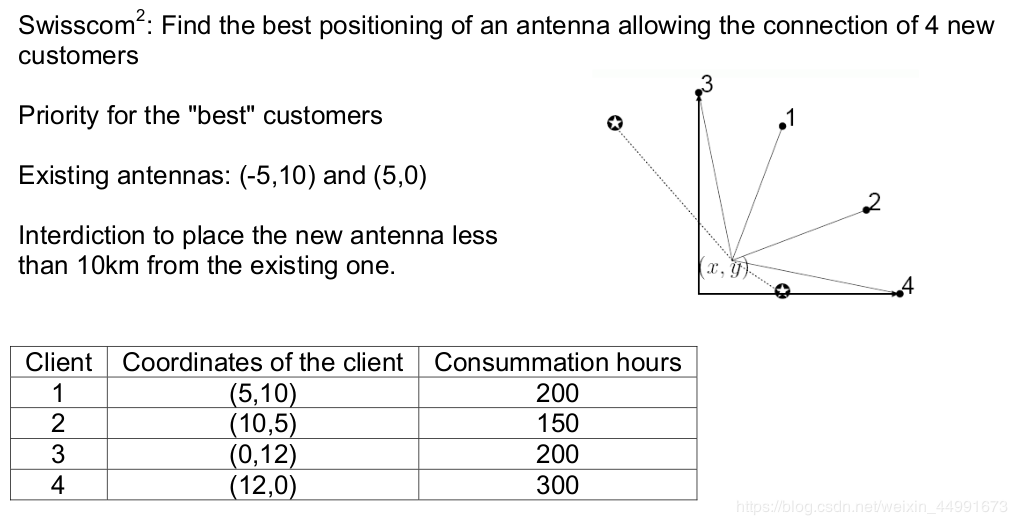
在这里插入图片描述
同时满足多个用户的要求，把多目标函数转化成一个目标函数。

EXAMPLE5:RR ROBOT

在这里插入图片描述
用等高线分析，不同出发点可能会逼近不同的结果，我们很难寻找到全局极值点。

EXAMPLE6:RESOURCES ALLOCATION

在这里插入图片描述
如何把数学问题用符号来表达，尤其是涉及类似棋盘位置的问题。

Matlab代码基础格式

%%start
x = -2:.2:2;
y=x;
[x1,x2]=meshgrid(x,y);
Z = 200*norm([x1-5,x2-10])+150*norm([x1-10,x2-5])+200*norm([x1,x2-12])+300*norm([x1-12,x2]);
surf(x1,x2,Z);
contourf(x1,x2,Z);
% [c,h] = contourf(x1,x2,Z);clabel(c,h);colorbar;
% ... ... (X,Y,Z,[20,40,80,100,'k--']) select the value of line on the figure 
x0=[0,0];
lb = [];% lower band
ub = [];% upper band
options =optimset('Display','iter','tolx',1.e-6,'MaxIter',40,'MaxFunEvals',200);
x = fminunc(@myfunc,x0,[],[],[],[],lb,ub,@myconstr,options);
%%
function f = myfunc (x)
  %   Find the best location of the new antennes Provity for the best Customers
  %   start from one point to find a best one
  %   对于objective function的选择是值得讨论的。
  %   1）min f(x) = dist(N,4)
  %   2) min f(x) = dist(N,1)+dist(N,3)
  %   3) min f(x) = weight of hours * dist(N,i)
  %   Variable X = (x1,x2) coord of the anntennes location
  f = 200*norm([x(1)-5,x(2)-10])+150*norm([x(1)-10,x(2)-5])+200*norm([x(1),x(2)-12])+300*norm([x(1)-12,x(2)]);
endfunction
%%
function [g,h] = myconstr (x)
  g(1) = 10 - norm([x(1)-5,x(2)]);
  g(2) = 10 - norm([x(1)+5,x(2)-10]);
  h = [];
endfunction

作者：肥鼠路易

最优化优化

1024 个赞